1 ClassD Audio Power Amplifiers Operation Efficiency EMC

1

Class-D Audio Power Amplifiers: Operation Efficiency EMC 2

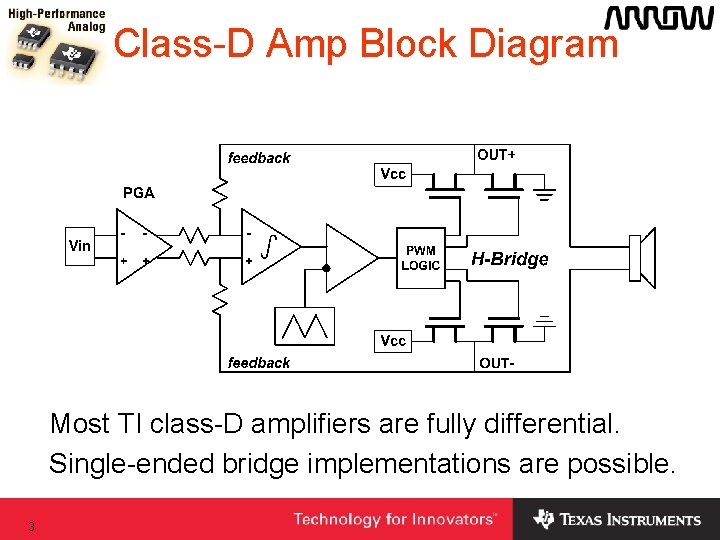
Class-D Amp Block Diagram Most TI class-D amplifiers are fully differential. Single-ended bridge implementations are possible. 3

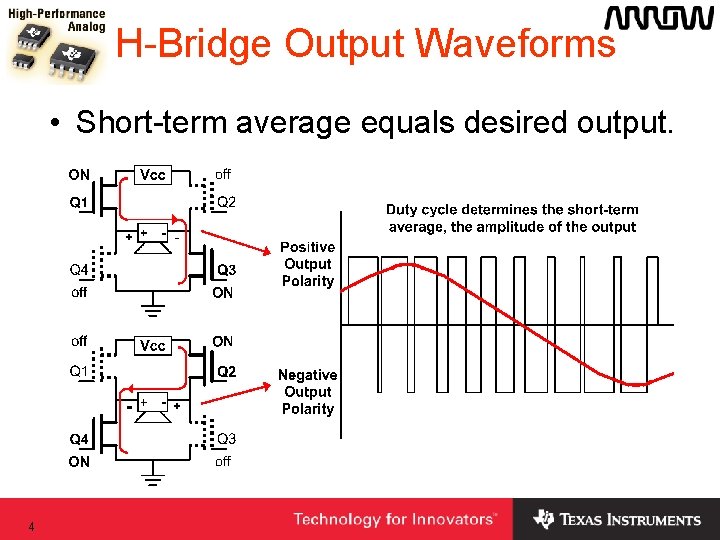
H-Bridge Output Waveforms • Short-term average equals desired output. 4

AD Modulation Ripple Current • AD modulation ripple current in the load reduces efficiency and increases required speaker power handling capacity. 5

BD (Filter-Free®) Modulation • BD modulation switches the outputs nearly in parallel when there is no signal. 6

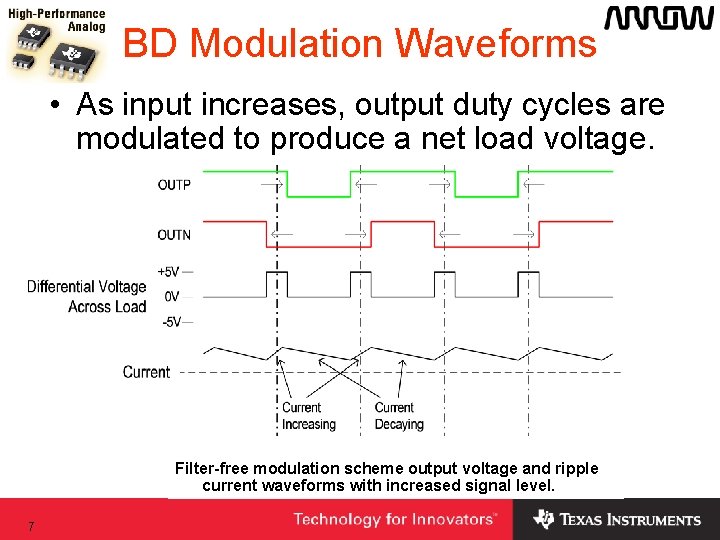
BD Modulation Waveforms • As input increases, output duty cycles are modulated to produce a net load voltage. Filter-free modulation scheme output voltage and ripple current waveforms with increased signal level. 7

BD Modulation Waveforms • As input increases, output duty cycles are modulated to produce a net load voltage. Filter-free modulation scheme output voltage and ripple current waveforms with increased signal level. 8

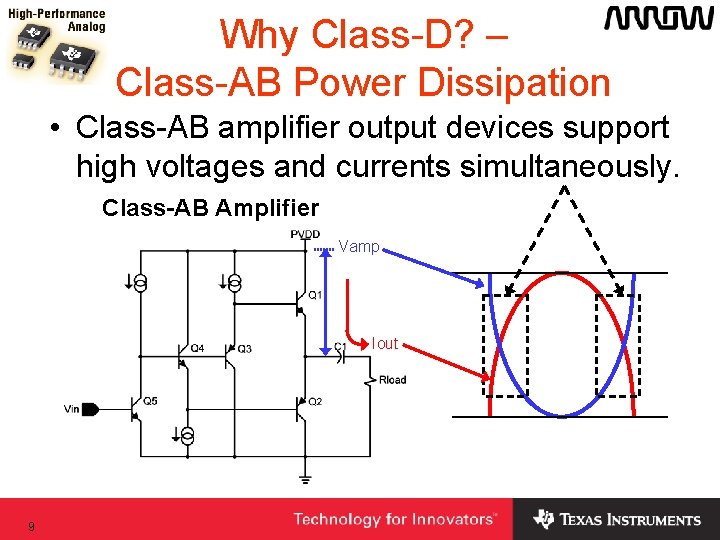
Why Class-D? – Class-AB Power Dissipation • Class-AB amplifier output devices support high voltages and currents simultaneously. Class-AB Amplifier Vamp Iout 9

Class-AB Power and Efficiency • BTL or differential output amplifier: • For a sine output: • Average power Vout = Vo sin(wt) to the load: Iout = Vout / Rload Pout = Vo ^ 2 2 Rload • Average power from the supply is • Net power in amp: Vps * Iout average: Pamp = Pps – Pout Pps = 2 Vps * Vo • Efficiency: Pout/Pps P Rload • Efficiency = P Vo 4 Vps 10

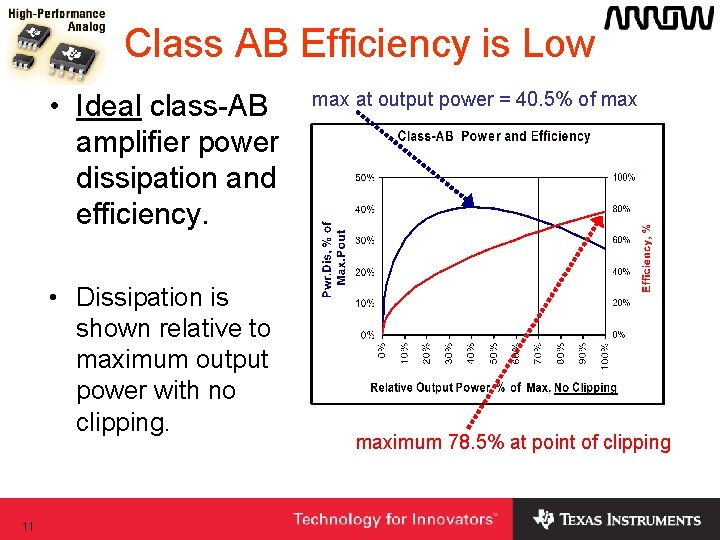
Class AB Efficiency is Low • Ideal class-AB amplifier power dissipation and efficiency. • Dissipation is shown relative to maximum output power with no clipping. 11 max at output power = 40. 5% of maximum 78. 5% at point of clipping

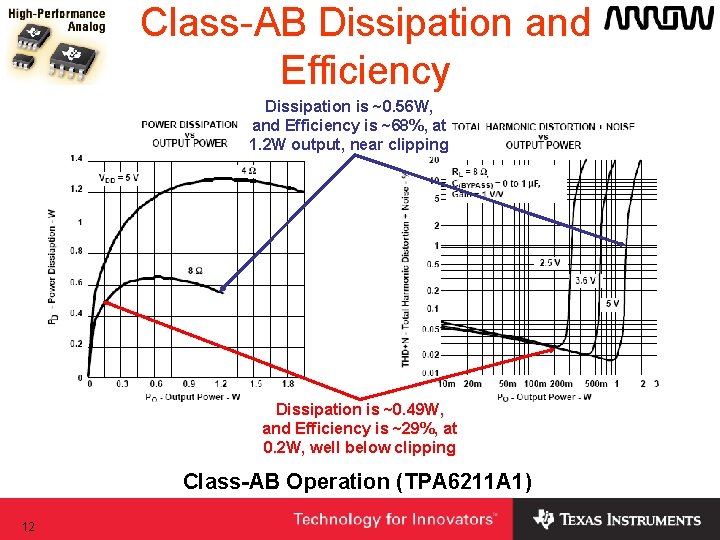
Class-AB Dissipation and Efficiency Dissipation is ~0. 56 W, and Efficiency is ~68%, at 1. 2 W output, near clipping Dissipation is ~0. 49 W, and Efficiency is ~29%, at 0. 2 W, well below clipping Class-AB Operation (TPA 6211 A 1) 12

Class-D Power Losses • In Class-D amplifiers most power losses occur in the output devices, typically FETs with low on resistances. 13

Class-D Efficiency • At high output levels, Class-D amplifier efficiency depends only on a resistor ratio, so it is essentially constant. Efficiency = Pout = Rload. Pout + Pamp Rload + Rfet • Switching edges and quiescent currents contribute only small losses, so they affect efficiency only at the lowest power levels. 14

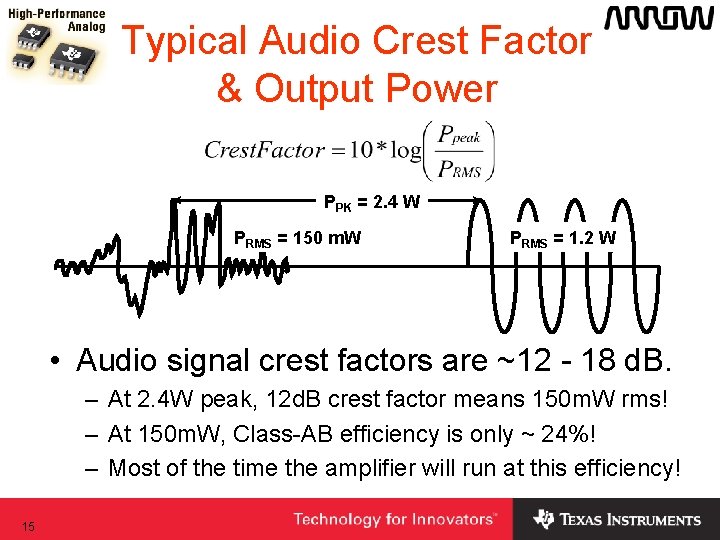
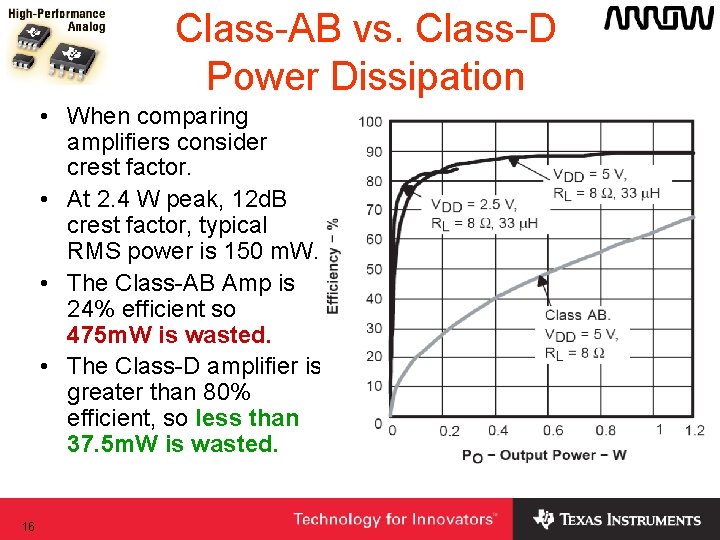
Typical Audio Crest Factor & Output Power PPK = 2. 4 W PRMS = 150 m. W PRMS = 1. 2 W • Audio signal crest factors are ~12 - 18 d. B. – At 2. 4 W peak, 12 d. B crest factor means 150 m. W rms! – At 150 m. W, Class-AB efficiency is only ~ 24%! – Most of the time the amplifier will run at this efficiency! 15

Class-AB vs. Class-D Power Dissipation • When comparing amplifiers consider crest factor. • At 2. 4 W peak, 12 d. B crest factor, typical RMS power is 150 m. W. • The Class-AB Amp is 24% efficient so 475 m. W is wasted. • The Class-D amplifier is greater than 80% efficient, so less than 37. 5 m. W is wasted. 16

RC Filter for Viewing Class-D Output • Filter frequency should be 30 to 40 k. Hz. • Possible RCs: 100 W/47 n. F; 330 W/18 n. F. 17

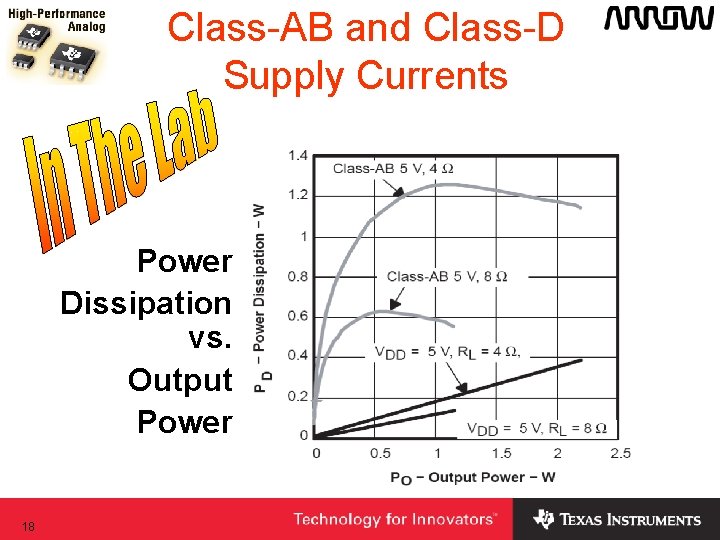
Class-AB and Class-D Supply Currents Power Dissipation vs. Output Power 18

Radiation by Cables & Traces • Cables and traces carrying RF currents act as antennas. • An antenna tends to produce a quasicircular electric field around its axis. 19

How EMI Occurs • EMI requires a generator that couples to another circuit where its signal is detected. • Output cables produce EMI radiation with horizontal orientation, and power and input cables do so with vertical orientation. 20

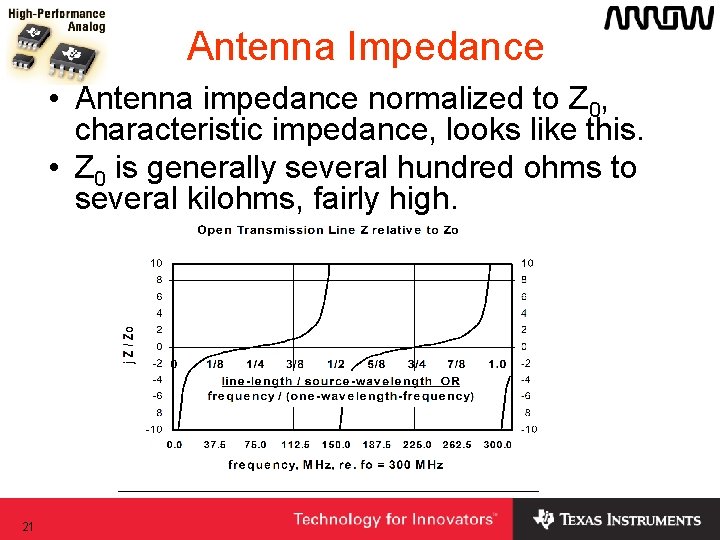
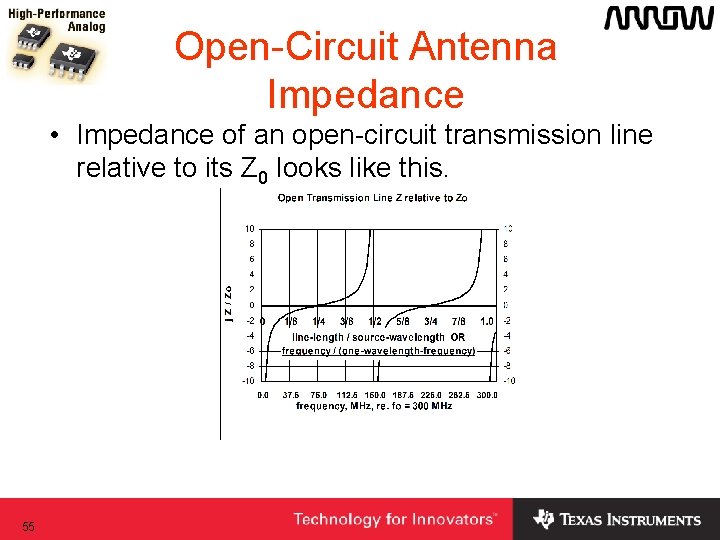
Antenna Impedance • Antenna impedance normalized to Z 0, characteristic impedance, looks like this. • Z 0 is generally several hundred ohms to several kilohms, fairly high. 21

Test Venue and Setup National Technical Systems’ FCC-certified 3 -meter chamber in Plano, Texas. Chamber / Antenna Setup 22 Turntable / EVM Setup from Rear

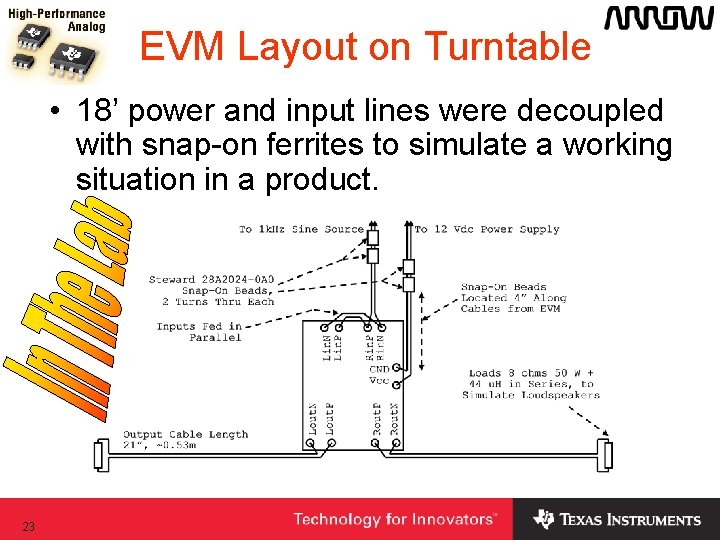
EVM Layout on Turntable • 18’ power and input lines were decoupled with snap-on ferrites to simulate a working situation in a product. 23

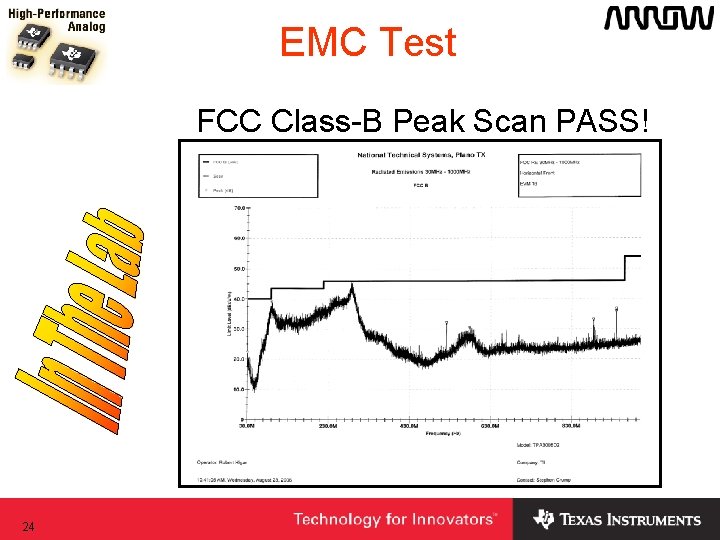
EMC Test FCC Class-B Peak Scan PASS! 24

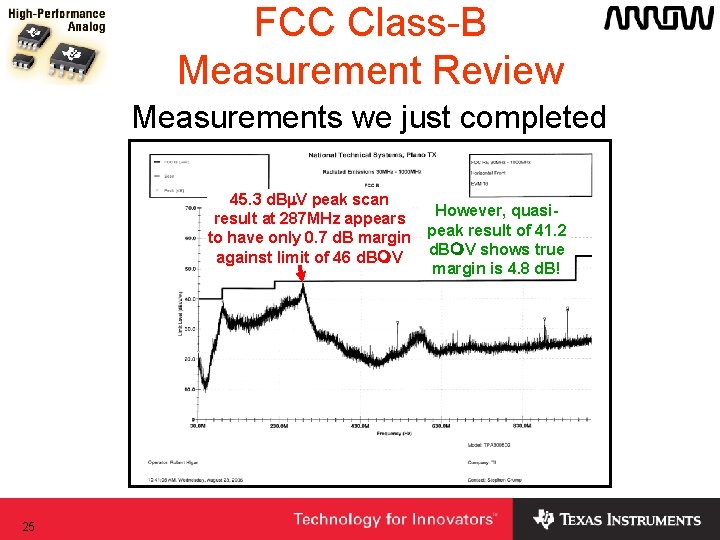
FCC Class-B Measurement Review Measurements we just completed 45. 3 d. Bm. V peak scan However, quasiresult at 287 MHz appears to have only 0. 7 d. B margin peak result of 41. 2 d. Bm. V shows true against limit of 46 d. Bm. V margin is 4. 8 d. B! 25

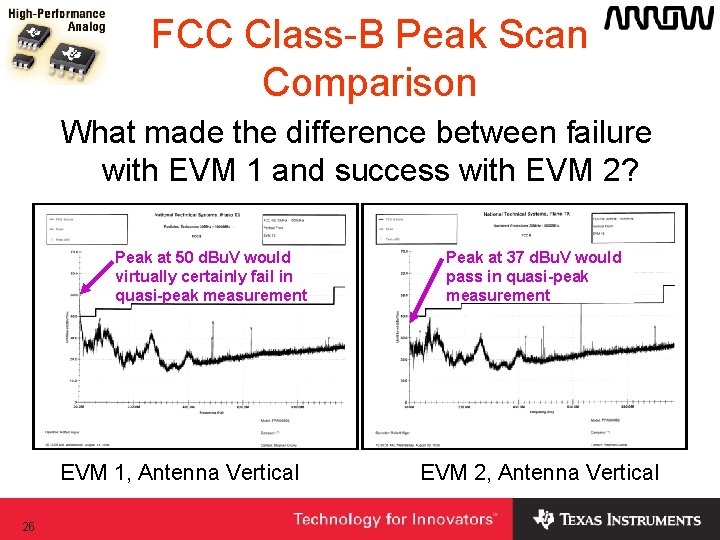
FCC Class-B Peak Scan Comparison What made the difference between failure with EVM 1 and success with EVM 2? Peak at 50 d. Bu. V would virtually certainly fail in quasi-peak measurement EVM 1, Antenna Vertical 26 Peak at 37 d. Bu. V would pass in quasi-peak measurement EVM 2, Antenna Vertical

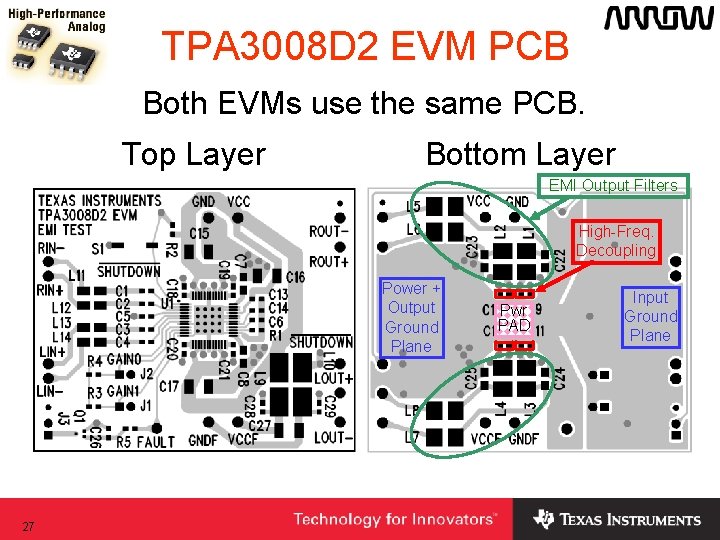
TPA 3008 D 2 EVM PCB Both EVMs use the same PCB. Top Layer Bottom Layer EMI Output Filters High-Freq. Decoupling Power + Output Ground Plane 27 Pwr PAD Input Ground Plane

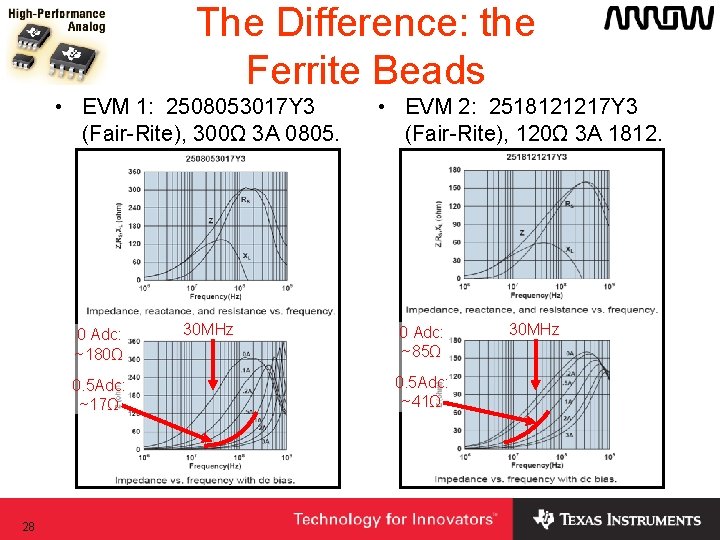
The Difference: the Ferrite Beads • EVM 1: 2508053017 Y 3 (Fair-Rite), 300Ω 3 A 0805. 0 Adc: ~180Ω 0. 5 Adc: ~17Ω 28 30 MHz • EVM 2: 2518121217 Y 3 (Fair-Rite), 120Ω 3 A 1812. 0 Adc: ~85Ω 0. 5 Adc: ~41Ω 30 MHz

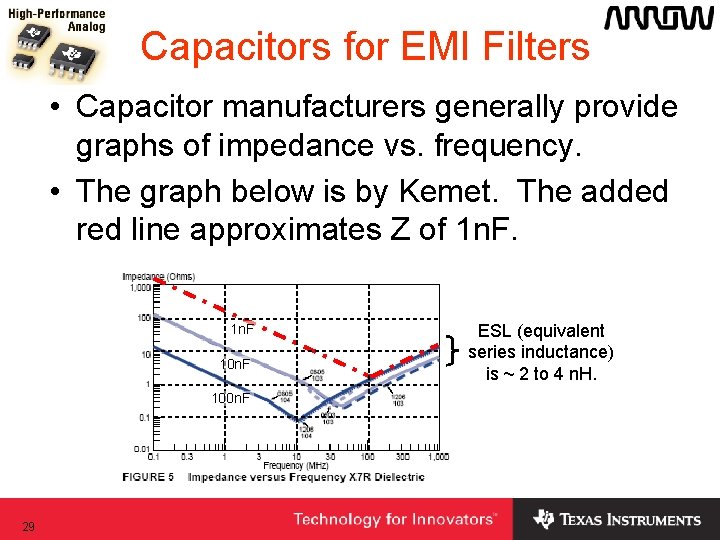
Capacitors for EMI Filters • Capacitor manufacturers generally provide graphs of impedance vs. frequency. • The graph below is by Kemet. The added red line approximates Z of 1 n. F 100 n. F 29 ESL (equivalent series inductance) is ~ 2 to 4 n. H.

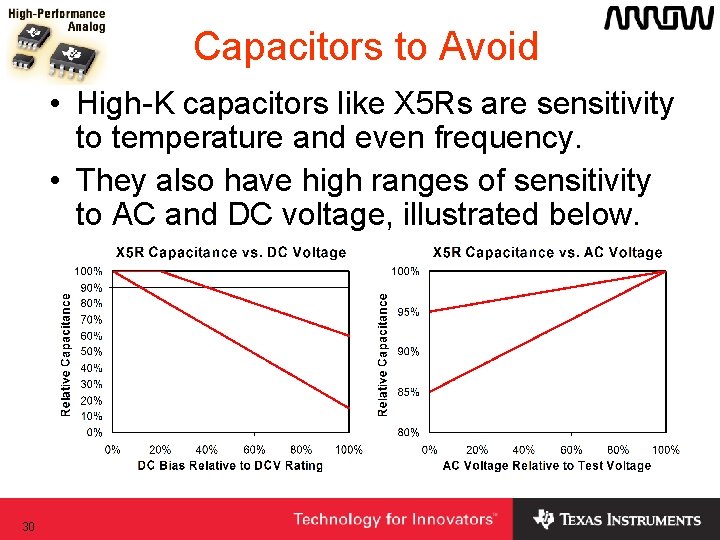
Capacitors to Avoid • High-K capacitors like X 5 Rs are sensitivity to temperature and even frequency. • They also have high ranges of sensitivity to AC and DC voltage, illustrated below. 30

Inductors for EMI Filters • Inductors saturate, and they self-resonate. • Low SFR will make ineffective EMI filters! 31

Rules for Picking Filter Components • Be aware of the various shortcomings and frequency limitations and make these part of your design. • Insist on full characterization before trying a part in a filter. • Try predicting actual attenuation from full characterization before spending some hours building and testing a filter. 32

Parasitics in PCB Layouts • Parasitics that promote EMI are mostly capacitive and inductive, coupling EMI currents into nearby traces and degrading decoupling and EMI filter components. • In 1 -oz copper, resistivity is ~ 0. 5 mΩ per square, usually not an issue. (Resistance of 1 -oz Cu is 0. 5 mΩ * length / area. ) • A trace 10 mils by 100 mils has low resistance, only about 5 milliohms. 33

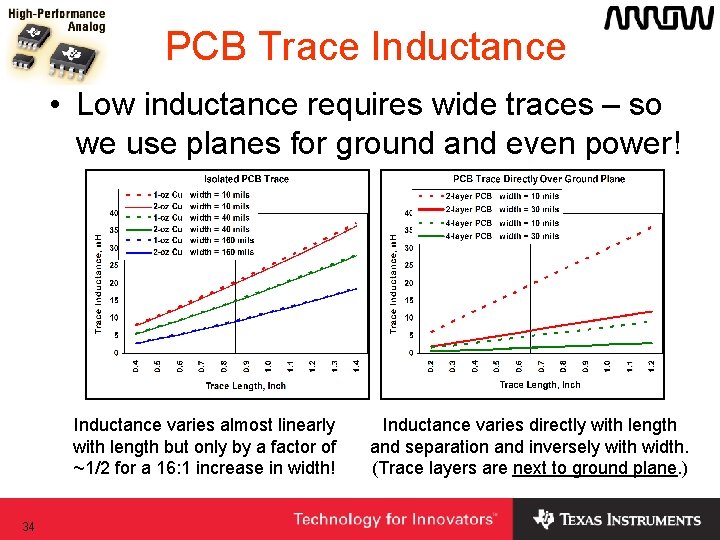
PCB Trace Inductance • Low inductance requires wide traces – so we use planes for ground and even power! Inductance varies almost linearly with length but only by a factor of ~1/2 for a 16: 1 increase in width! 34 Inductance varies directly with length and separation and inversely with width. (Trace layers are next to ground plane. )

Potential Impact On Components • Inductance of a 0. 3” long 10 mil trace over a 2 -layer PCB ground plane is about 9 n. H. • This is greater than for a typical SMD cap, 2 to 4 n. H, so it will dramatically degrade performance of the capacitor! • Circuit loops also add inductance. There is no easy measure here; smaller is better! 35

TPA 3008 D 2 EVM PCB Review Grounding is the single most critical factor. Top Layer Bottom Layer Power + Output Ground Plane 36 Pwr. P AD Input Ground Plane

TPA 3008 D 2 Ferrite Bead EMI Filters • TPA 3008 D 2 uses ferrite bead + capacitor EMI output filters, which work for output cable length up to about 21”, 0. 53 m. • In these filters a second bead on each output damps output cable resonances. 37

Why the Second Bead? • Without the second bead the output impedance of the filter is essentially inductive or capacitive. • Impedance zeros of the output cable will resonate with the shunt leg, driving its impedance high and drastically reducing filtering at those frequencies. 38

Inductor Filters • Higher power and longer cables may require inductors for compliance. • The filter below from our TPA 3100 D 2 EVM (20 W per channel at 10% THD) permitted it to pass FCC-B with wide margins. 39

TPA 3100 D 2 EVM PCB Review Again, grounding is the most critical factor. Top Layer Bottom Layer Output EMI Inductors 40 Decoupling Caps Output EMI Caps

Additional Resources www. ti. com/analog www. arrow. com 41

APPENDIX 1 PCB Layout for EMC 42

PCB Layout for EMC • Use a ground plane to minimize ground inductances. • Use a star ground concept centered on the primary switching chip with the Power. PAD as star ground center point when it is provided. • Place high-frequency decoupling caps as close as feasible to the chip to minimize trace inductance. 43

PCB Layout for EMC Cont’d. • Place high-frequency decoupling caps and EMI filter caps on the ground plane layer to minimize ground return inductance. • Confine power and output currents to a separate section of ground plane, away from input circuits, both digital and analog! – EMI-inducing currents can be radiated into either type of input. – Switching edges can corrupt clock and data lines, causing increases in noise and THD. 44

PCB Layout for EMC Cont’d. • Route traces through pads of decoupling and filter caps, not from other elements. • Try to avoid vias in traces for high currents and for decoupling and EMI filter caps. Double them if they must be used in traces for high currents. (Via impedance carries some uncertainty. ) • Locate EMI filters at the circuits they filter, not at a distance. The intervening traces are antennas! 45

PCB Layout for EMC Cont’d. • Avoid PCB trace lengths that are closely related to wavelengths of primary power frequencies. • We have seen GSM interference in input traces 1. 5”, 3. 8 cm, long, roughly the quarter wavelength of GSM frequency 1900 MHz (wavelength ~= 0. 15 m or 6”!). • In such a case, reflections reinforce each other to create a relatively large voltage. 46

APPENDIX 2 Antennas 47

Radiation & Impedance • Simple Antenna Radiation Pattern • Simple Antenna Impedance Pattern – A good engineering text on electromagnetism is a useful reference. I used a book called Applied Electromagnetism, by Shen & Kong, from PWS Publishers. 48

Simple Antenna Radiation Pattern • A dipole antenna produces the following cross-sectional field strength pattern at constant radius from the antenna center. For antenna lengths less than 1/2 wavelength: |Eo| ~= ω μ | I | L |sin θ| / ( 4π r ), where • ω is angular frequency, • μ is permeability of surrounding medium, in our case generally free space, • I is current in the antenna, defined to flow vertically on the Z axis, • L is antenna length, • θ is the angle of “r” with respect to the vertical, Z, axis, and • r is the radius of the measurement point from the center of the antenna. The field vector direction is that of increasing θ. 49

Dipole Field Characteristics • The pattern is like a donut with an infinitely narrow hole. • Field strength varies inversely with r and directly with I, ω, L and |sin θ|. – Antenna length less than a half wavelength produce the field pattern shown above. – Antenna length of a half wavelength produces very nearly the same pattern. – Antenna length more than a half wavelength produces multiple lobes with nulls between. 50

Consequences of Dipole Pattern • Higher currents and higher frequencies produce higher fields. • Longer antennas produce (and collect!) higher fields (they are more “efficient”). • Components, wires and PCB traces lying parallel to the axis of a current-carrying antenna see the highest electric field strengths and induced voltages. 51

Antennas Are Everywhere • Input, power and output cables constitute antennas and can radiate EMI if they are not appropriately filtered. • Traces on PCBs also constitute antennas and can have the same undesirable effect. • So, filter input, power and output lines as required and locate filters as close as possible to the generators they address. 52

Simple Antenna Impedance Pattern • Impedance of a dipole antenna over a ground plane may be approximated using transmission line theory. • Characteristic impedance, which applies at low frequency, is typically a couple of hundred ohms to several kilohms. • Since all current generated in an antenna must be reflected from its ends, we can use reflection patterns to predict relative impedance versus frequency. 53

Open-Circuit Transmission Line • Voltage is reflected from the open circuit in phase with the input voltage, so V = V 0 ( e-jkz + ejkz ) = 2 V 0 cos(kz). (k is a wave number equal to 2 pi / λ, wavelength. ) • Current is reflected out of phase, so I = V 0 ( e-jkz - ejkz ) / Z 0 = 2 j V 0 sin(kz). • Their ratio is transmission line impedance vs. frequency, so Z = Z 0 / ( j tan(kz) ). 54

Open-Circuit Antenna Impedance • Impedance of an open-circuit transmission line relative to its Z 0 looks like this. 55

Antenna Impedance Effects • Remember that this is an approximation: it’s altered by influences like end effects and other conductors nearby (transmission line analysis assumes infinite length and a perfect layout!). • Antenna impedance periodically changes from capacitive to inductive with a zero at each transition. • Near its zeros antenna impedance adds complex elements to EMI filters. 56

Antenna Impedance Effects Cont’d. • At the resonances that result, the antenna will draw relatively large currents and will radiate strongly, producing EMI peaks. • These resonances also can interact with EMI filters at frequencies that depend on the phase of the filter’s output impedance. • Damping in the environment and the EMI filter and PCB layout, always present, will limit magnitude of these peaks. 57

APPENDIX 3 Formulas for PCB Trace Inductance & Via Impedance 58

Inductance of Isolated PCB Traces • Inductance of an isolated PCB trace can be computed as follows, for inches & cm. L ~= 5 l [ ln(l/(w+t))+1/2 ] n. H, in L ~= 2 l [ ln(l/(w+t))+1/2 ] n. H, cm ( l, w & t are trace length, width and thickness) • Inductance is roughly linear with length. • However, because of the logarithmic factor, inductance is insensitive to trace width and thickness. (Thickness especially has little effect. ) 59

PCB Trace Over a Ground Plane • Inductance of a PCB trace directly over a ground plane can be computed as follows. L ~= 5 lh/w n. H/in, inches L ~= 2 lh/w n. H/cm, cm ( l, w & h are trace length, width and separation from the ground plane) • L varies directly with length and separation from ground and inversely with width. • It’s possible to achieve much lower inductance in this configuration. 60

Via Impedance • Inductance (h & d = height and diameter). L ~= 5 h [ ln(4 h/d)+1 ] n. H/in, inches • Resistance (ρ is copper resistivity, 2. 36 e-6 ohm-inch, l is via length & A is copper annular area) R ~= ρl/A, inches • 20 -mil via, 1 -mil plating, in 0. 06” PCB: L ~= 5*0. 06*(ln(4*0. 06/0. 019)+1) ~= 1. 1 n. H R ~= ρ*0. 06/(pi*(0. 01^2 -0. 009^2)) ~= 2. 4 mohm 61