1 Chapter 7 Steady magnetic field EMLAB 2

1 Chapter 7. Steady magnetic field EMLAB
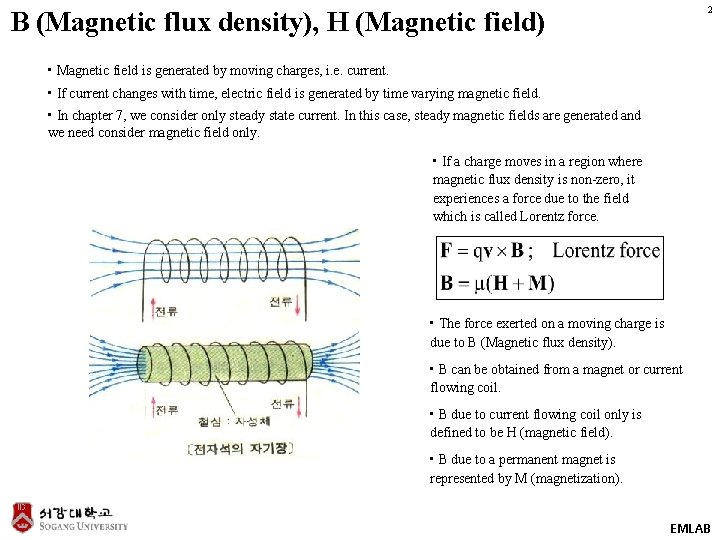
2 B (Magnetic flux density), H (Magnetic field) • Magnetic field is generated by moving charges, i. e. current. • If current changes with time, electric field is generated by time varying magnetic field. • In chapter 7, we consider only steady state current. In this case, steady magnetic fields are generated and we need consider magnetic field only. • If a charge moves in a region where magnetic flux density is non-zero, it experiences a force due to the field which is called Lorentz force. • The force exerted on a moving charge is due to B (Magnetic flux density). • B can be obtained from a magnet or current flowing coil. • B due to current flowing coil only is defined to be H (magnetic field). • B due to a permanent magnet is represented by M (magnetization). EMLAB
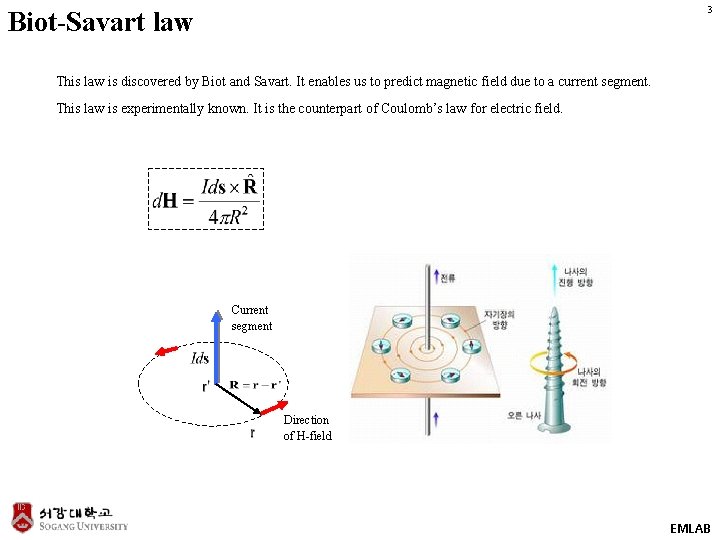
3 Biot-Savart law This law is discovered by Biot and Savart. It enables us to predict magnetic field due to a current segment. This law is experimentally known. It is the counterpart of Coulomb’s law for electric field. Current segment Direction of H-field EMLAB
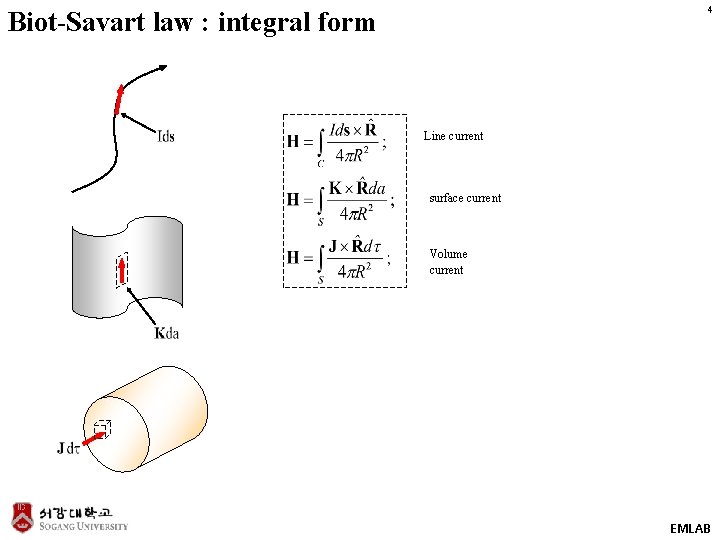
4 Biot-Savart law : integral form Line current surface current Volume current EMLAB

Magnetic field due to an infinitely long line current 5 • An infinitely long straight current flowing in the z-axis. odd function EMLAB

Magnetic field due to a finitely long current filament 6 기함수 EMLAB
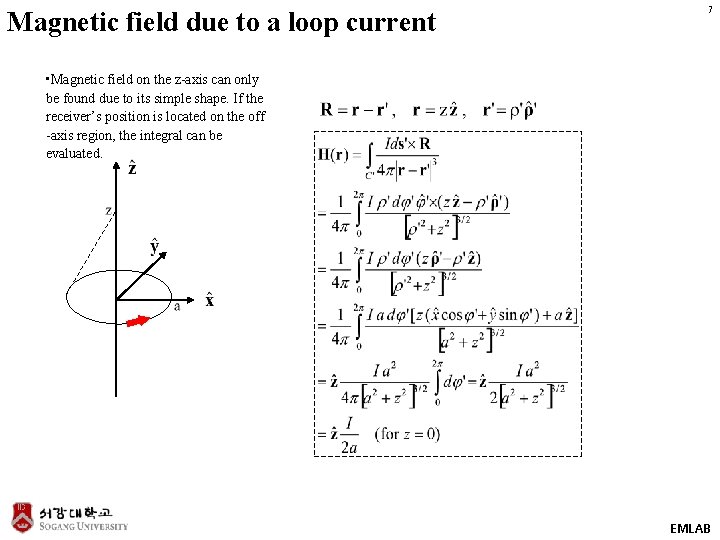
Magnetic field due to a loop current 7 • Magnetic field on the z-axis can only be found due to its simple shape. If the receiver’s position is located on the off -axis region, the integral can be evaluated. EMLAB

Calculation of H of a solenoid 8 Surface current density If a copper wire is wound around a cylinder N times in the length d and current I is flowing through it, it can be approximated by a surface current along direction with a magnitude K = NI/d. EMLAB
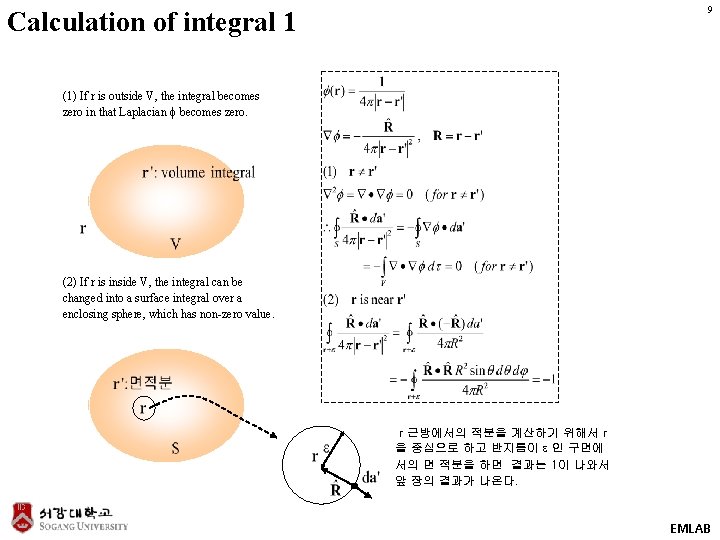
9 Calculation of integral 1 (1) If r is outside V, the integral becomes zero in that Laplacian ϕ becomes zero. (2) If r is inside V, the integral can be changed into a surface integral over a enclosing sphere, which has non-zero value. r 근방에서의 적분을 계산하기 위해서 r 을 중심으로 하고 반지름이 인 구면에 서의 면 적분을 하면 결과는 1이 나와서 앞 장의 결과가 나온다. EMLAB

10 Ampere’s law • Ampere law facilitates calculation of mangetic field like the Gauss law for electric field. . • Unlike Gauss’ law, Ampere’s law is related to line integrals. • Ampere’s law is discovered experimentally and states that a line integral over a closed path is equal to a current flowing through the closed loop. • In the left figure, line integrals of H along path a and b is equal to I because the paths enclose current I completely. But the integral along path c is not equal to I because it does not encloses completely the current I. EMLAB

11 Example- Coaxial cable • The direction of magnetic fields can be found from right hand rule. • The currents flowing through the inner conductor and outer sheath should have the same magnitude with different polarity to minimize the magnetic flux leakage EMLAB
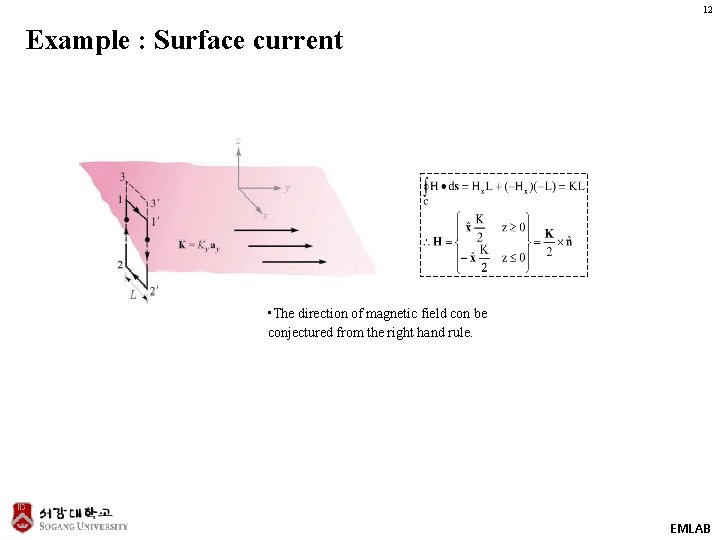
12 Example : Surface current • The direction of magnetic field con be conjectured from the right hand rule. EMLAB
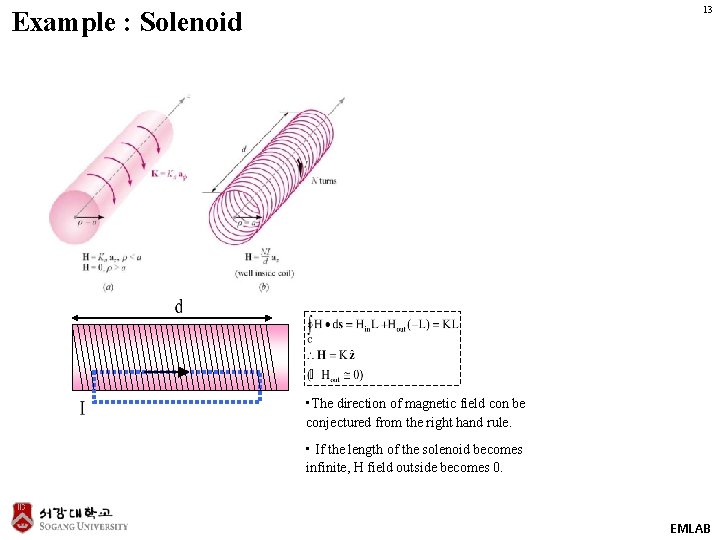
13 Example : Solenoid • The direction of magnetic field con be conjectured from the right hand rule. • If the length of the solenoid becomes infinite, H field outside becomes 0. EMLAB
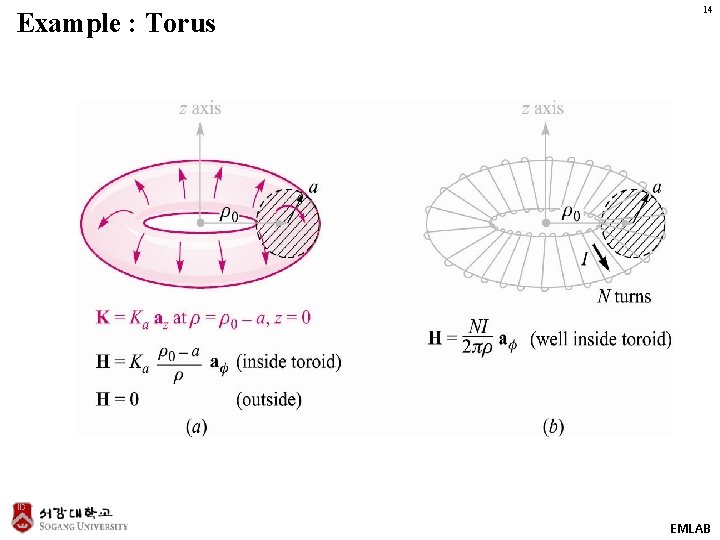
Example : Torus 14 EMLAB

15 Example problem 8. 18 A wire of 3 -mm radius is made up of an inner material (0 < ρ < 2 mm) for which σ = 107 S/m, and an outer material (2 mm < ρ < 3 mm) for which σ = 4× 107 S/m. If the wire carries a total current of 100 m. A dc, determine H everywhere as a function of ρ. 2 100 m. A 1 2 mm EMLAB

Example problem 8. 9 16 EMLAB

Example problem 8. 6 17 EMLAB
- Slides: 17