1 Chapter 7 Linear algebra EMLAB Basics of

1 Chapter 7. Linear algebra EMLAB
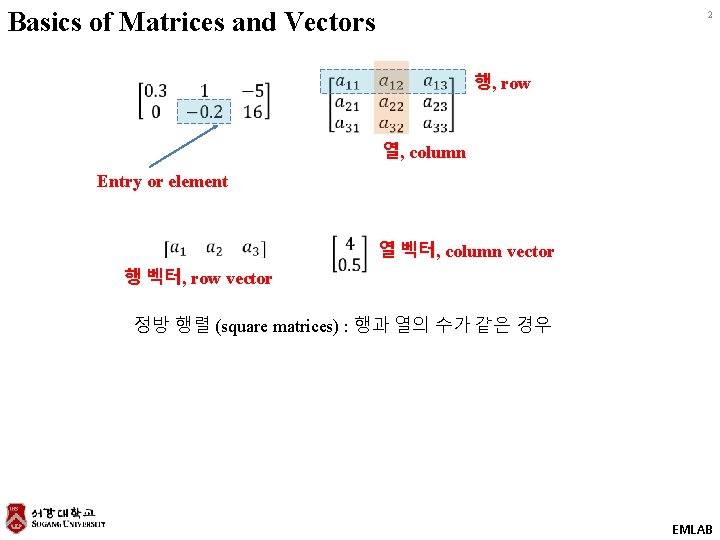
Basics of Matrices and Vectors 2 행, row 열, column Entry or element 열 벡터, column vector 행 벡터, row vector 정방 행렬 (square matrices) : 행과 열의 수가 같은 경우 EMLAB

General Concepts and Notations 3 Diagonal of A EMLAB

4 EXAMPLE 1 Linear Systems, a Major Application of Matrices EXAMPLE 2 Sales Figures in Matrix Form Sales figures for three products I, III in a store on Monday (Mon), Tuesday (Tues), may for each week be arranged in a matrix. Mon Tues Wed Thur Fri Sat Sun I II III EMLAB

Addition and Scalar Multiplication of Matrices and Vectors 5 Addition of Matrices EXAMPLE 4 Addition of Matrices and Vectors EMLAB

6 Scalar Multiplication (Multiplication by a Number) EXAMPLE 4 Scalar Multiplication Rules for Matrix Addition and Scalar Multiplication EMLAB

7. 2 Matrix Multiplication 7 Multiplication of a Matrix by a Matrix EMLAB

EXAMPLE 1 Matrix Multiplication 8 EXAMPLE 2 Multiplication of a Matrix and a Vector EXAMPLE 3 Products of Row and Column Vectors EMLAB

9 EXAMPLE 5 Product in Terms of Row and Column Vectors EMLAB
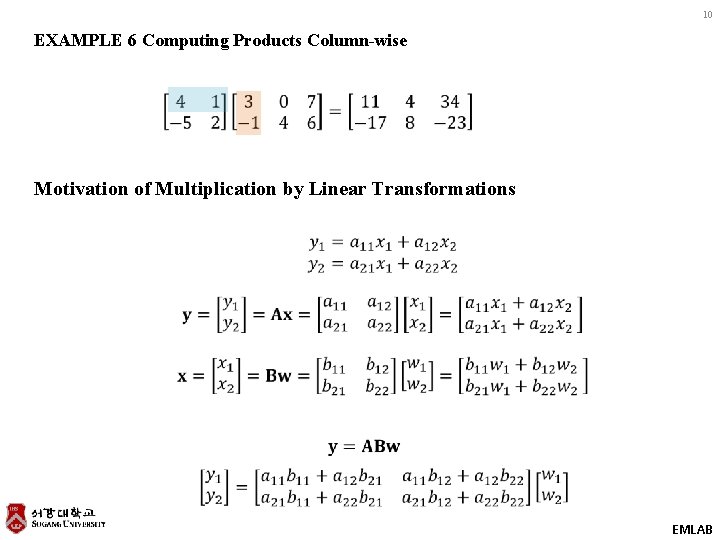
10 EXAMPLE 6 Computing Products Column-wise Motivation of Multiplication by Linear Transformations EMLAB

Transposition 11 We obtain the transpose of a matrix by writing its rows as columns (or equivalently its columns as rows). Transposition of Matrices and Vectors EMLAB

Symmetric and Skew-Symmetric Matrices 12 • Symmetric matrices are square matrices whose transpose equals the matrix itself. • Skew-symmetric matrices are square matrices whose transpose equals minus the matrix Upper and Lower Triangular Matrices Upper triangular matrices are square matrices that can have nonzero entries only on and above the main diagonal, whereas any entry below the diagonal must be zero. Upper triangular Lower triangular EMLAB

7. 3 Linear Systems of Equations. Gauss Elimination 13 Augmented matrix EMLAB

Elementary Row Operations. Row-Equivalent Systems 14 Elementary Row Operations for Matrices: 1. Interchange of two rows 2. Addition of a constant multiple of one row to another row 3. Multiplication of a row by a nonzero constant c Row-Equivalent Systems Row-equivalent linear systems have the same set of solutions. EMLAB

Gauss Elimination and Back Substitution 15 Consider a linear system that is in triangular form (in full, upper triangular form) such as EMLAB
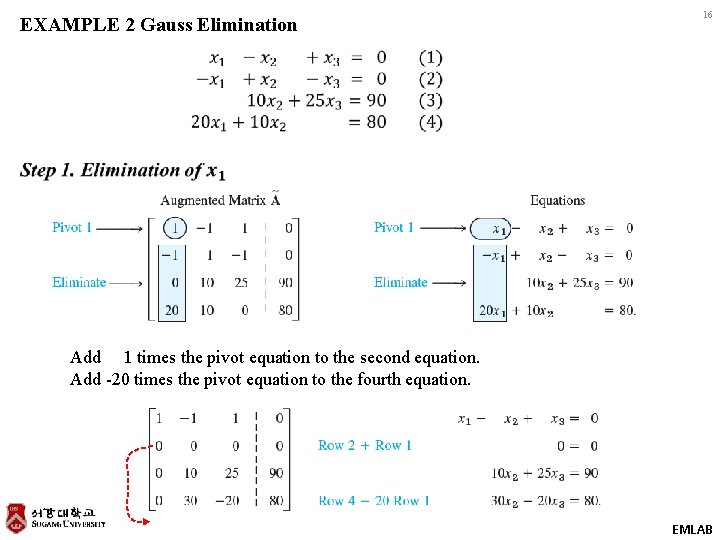
EXAMPLE 2 Gauss Elimination 16 Add 1 times the pivot equation to the second equation. Add -20 times the pivot equation to the fourth equation. EMLAB

17 Add -3 times the pivot equation to the third equation. EMLAB

EXAMPLE 3 Gauss Elimination if Infinitely Many Solutions Exist 18 Solve the following linear system of three equations in four unknowns whose augmented matrix is EMLAB

19 EMLAB

EXAMPLE 4 Gauss Elimination if no Solution Exists 20 EMLAB

Row Echelon Form and Information From It 21 Row echelon form : Rows of zeros, if present, are the last rows, and, in each nonzero row, the leftmost nonzero entry is farther to the right than in the previous row. For instance, and At the end of the Gauss elimination (before the back substitution), the row echelon form of the augmented matrix will be The number of nonzero rows, r, in the row-reduced coefficient matrix R is called the rank of R and also the rank of A. EMLAB

22 EMLAB

7. 4 Linear Independence. Rank of a Matrix. Vector Space 23 Linear Independence and Dependence of Vectors Rank of a Matrix The rank of a matrix A is the maximum number of linearly independent row vectors of A. It is denoted by rank A. THEOREM 1 Row-Equivalent Matrices : Row-equivalent matrices have the same rank. EMLAB

EXAMPLE 1 Linear Independence and Dependence 24 The three vectors are linearly dependent because The first two of the three vectors are linearly independent because EXAMPLE 2 Rank The matrix has rank 2, because Example 1 shows that the first two row vectors are linearly independent, whereas all three row vectors are linearly dependent. EMLAB

EXAMPLE 3. Determination of Rank 25 The last matrix is in row-echelon form and has two nonzero rows. Hence rank as before. EMLAB

26 THEOREM 2 Linear Independence and Dependence of Vectors Consider p vectors that each have n components. Then these vectors are linearly independent if the matrix formed, with these vectors as row vectors, has rank p. However, these vectors are linearly dependent if that matrix has rank less than p. THEOREM 3 Rank in Terms of Column Vectors EMLAB

27 EMLAB

28 and collect components in columns. Indeed, we can write EMLAB

29 THEOREM 4 Linear Dependence of Vectors EMLAB

Vector Space 30 Conditions for a vector space • Dimension of a vector space : maximum number of linearly independent vectors in V • Basis : A linearly independent set in V consisting of a maximum possible number of vectors in V • Span : The set of all linear combinations of given basis vectors EMLAB

31 Row space of A : the span of the row vectors. (For an arbitrary matrix A) Column space of A : the span of the column vectors. THEOREM 6 Row Space and Column Space The row space and the column space of a matrix A have the same dimension, equal to rank A + nullity A = Number of columns of A. EMLAB

7. 7 Determinants. Cramer’s Rule cofactor 32 minor EMLAB

33 Levi-Civita symbol EMLAB

34 EXAMPLE 1 Minors and Cofactors of a Third-Order Determinant EXAMPLE 2 Expansions of a Third-Order Determinant EXAMPLE 3 Determinant of a Triangular Matrix EMLAB

EXAMPLE 4 Evaluation of Determinants by Reduction to Triangular Form 35 EMLAB

36 Geometric meaning EMLAB
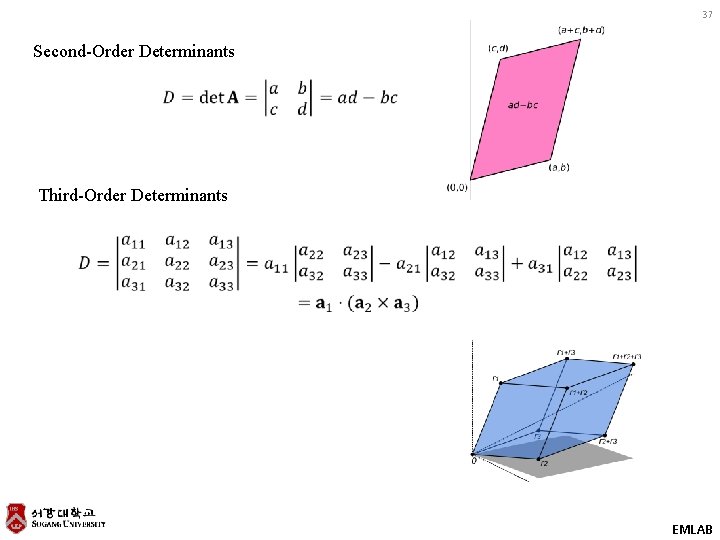
37 Second-Order Determinants Third-Order Determinants EMLAB

General Properties of Determinants 38 EMLAB



41 EMLAB

Cramer’s Rule 42 THEOREM 1 : Cramer’s Theorem (Solution of Linear Systems by Determinants) EMLAB

43 Proof Expanding D by its kth column, we obtain EMLAB

Cramer’s Rule for Linear Systems of Two Equations 44 EXAMPLE 1 Cramer’s Rule for Two Equations EMLAB

Cramer’s Rule for Linear Systems of Three Equations 45 EMLAB

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination 46 In this section we consider square matrices exclusively. EMLAB

Determination of the Inverse by the Gauss–Jordan Method 47 Using A, we form n linear systems EMLAB

48 EMLAB
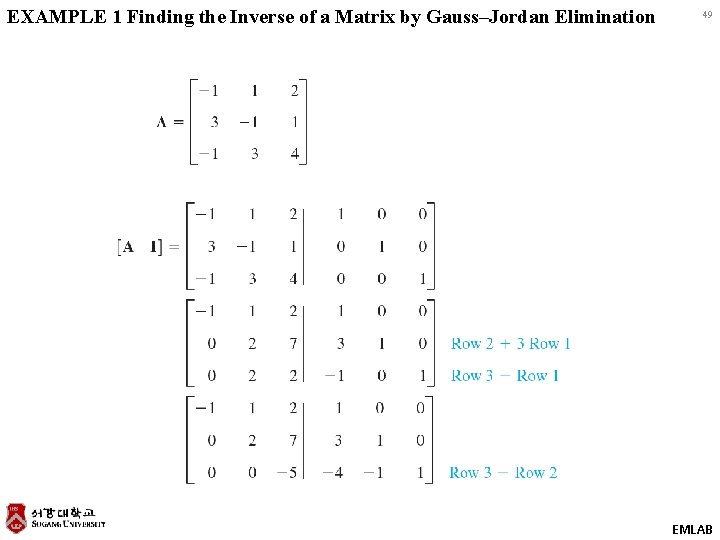
EXAMPLE 1 Finding the Inverse of a Matrix by Gauss–Jordan Elimination 49 EMLAB

50 EMLAB

THEOREM 2 Inverse of a Matrix by Determinants 51 EMLAB

Inverse of a product of matrices 52 Products can be inverted by taking the inverse of each factor and multiplying these inverses in reverse order, Proof : THEOREM 3 Cancellation Laws EMLAB
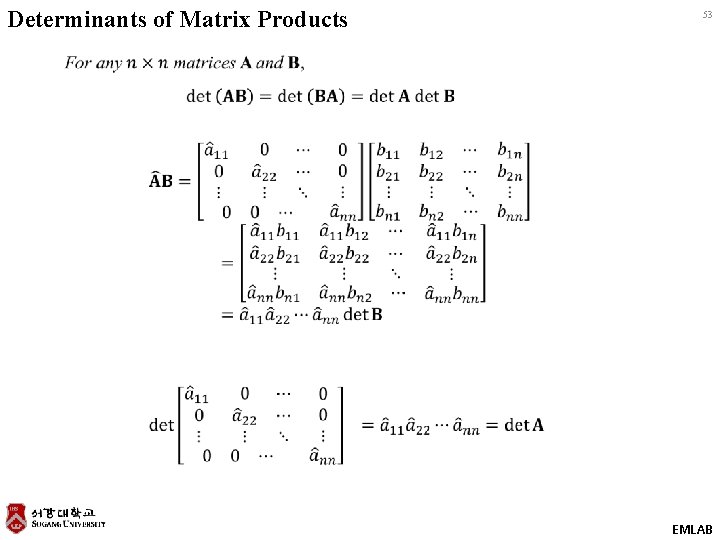
Determinants of Matrix Products 53 EMLAB
- Slides: 53