1 Chapter 3 MaximumLikelihood and Bayesian Parameter Estimation

1 Chapter 3: Maximum-Likelihood and Bayesian Parameter Estimation (part 2) l Bayesian Estimation (BE) l Bayesian Parameter Estimation: Gaussian Case l Bayesian Parameter Estimation: General Estimation l Problems of Dimensionality l Computational Complexity l Component Analysis and Discriminants l Hidden Markov Models

l 2 Bayesian Estimation (Bayesian learning to pattern classification problems) In MLE was supposed fixed l In BE is a random variable l The computation of posterior probabilities P( i | x) lies at the heart of Bayesian classification l Goal: compute P( i | x, D) Given the sample D, Bayes formula can be l written as: Pattern Classification, Chapter 3 2 3

3 l To demonstrate the preceding equation, use: Pattern Classification, Chapter 3 3 3

4 l Bayesian Parameter Estimation: Gaussian Case Goal: Estimate using the a-posteriori density P( | D) l The univariate case: P( | D) is the only unknown parameter Pattern Classification, Chapter 3 4 4

5 l Reproducing density Identifying (1) and (2) yields: Pattern Classification, Chapter 3 5 4

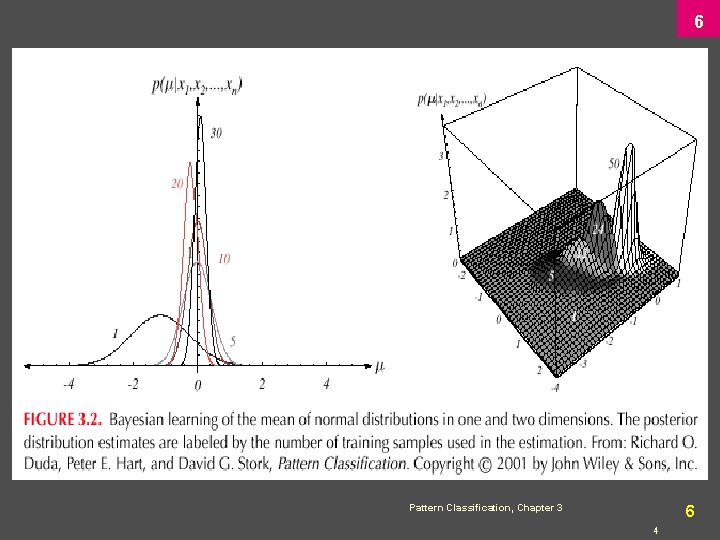
6 Pattern Classification, Chapter 3 6 4

7 l The univariate case P(x | D) l P( | D) computed l P(x | D) remains to be computed! It provides: (Desired class-conditional density P(x | Dj, j)) Therefore: P(x | Dj, j) together with P( j) And using Bayes formula, we obtain the Bayesian classification rule: Pattern Classification, Chapter 3 7 4

8 l Bayesian Parameter Estimation: General Theory l P(x | D) computation can be applied to any situation in which the unknown density can be parametrized: the basic assumptions are: form of P(x | ) is assumed known, but the value of is not known exactly l Our knowledge about is assumed to be contained in a known prior density P( ) l The rest of our knowledge is contained in a set D of n random variables x 1, x 2, …, xn that l The follows P(x) Pattern Classification, Chapter 3 8 5

9 The basic problem is: “Compute the posterior density P( | D)” then “Derive P(x | D)” Using Bayes formula, we have: And by independence assumption: Pattern Classification, Chapter 3 9 5

10 l Problems of Dimensionality l Problems involving 50 or 100 features (binary valued) l Classification accuracy depends upon the dimensionality and the amount of training data l Case of two classes multivariate normal with the same covariance Pattern Classification, Chapter 3 10 7

11 l If features are independent then: l Most useful features are the ones for which the difference between the means is large relative to the standard deviation l It has frequently been observed in practice that, beyond a certain point, the inclusion of additional features leads to worse rather than better performance: we have the wrong model ! Pattern Classification, Chapter 3 11 7

12 7 Pattern Classification, Chapter 3 12 7

13 l Computational Complexity l Our design methodology is affected by the computational difficulty l “big oh” notation f(x) = O(h(x)) “big oh of h(x)” If: (An upper bound on f(x) grows no worse than h(x) for sufficiently large x!) f(x) = 2+3 x+4 x 2 g(x) = x 2 f(x) = O(x 2) Pattern Classification, Chapter 3 13 7

14 l “big oh” is not unique! f(x) = O(x 2); f(x) = O(x 3); f(x) = O(x 4) l“big theta” notation f(x) = (h(x)) If: f(x) = (x 2) but f(x) (x 3) Pattern Classification, Chapter 3 14 7

15 l Complexity of the ML Estimation l Gaussian priors in d dimensions classifier with n training samples for each of c classes l For each category, we have to compute the discriminant function Total = O(d 2. . n) Total for c classes = O(cd 2. n) O(d 2. n) l Cost increase when d and n are large! Pattern Classification, Chapter 3 15 7

16 l Component Analysis and Discriminants Combine features in order to reduce the dimension of the feature space l Linear combinations are simple to compute and tractable l Project high dimensional data onto a lower dimensional space l Two classical approaches for finding “optimal” linear transformation l l PCA (Principal Component Analysis) “Projection that best represents the data in a least- square sense” l MDA (Multiple Discriminant Analysis) “Projection that best separates the data in a least-squares sense” Pattern Classification, Chapter 3 16 8

17 l Hidden Markov Models: Markov Chains l Goal: make a sequence of decisions l l Processes that unfold in time, states at time t are influenced by a state at time t-1 l Applications: speech recognition, gesture recognition, parts of speech tagging and DNA sequencing, l Any temporal process without memory T = { (1), (2), (3), …, (T)} sequence of states We might have 6 = { 1, 4, 2, 1, 4} l The system can revisit a state at different steps and not every state need to be visited Pattern Classification, Chapter 3 17 10

18 l First-order Markov models l Our productions of any sequence is described by the transition probabilities P( j(t + 1) | i (t)) = aij Pattern Classification, Chapter 3 18 10

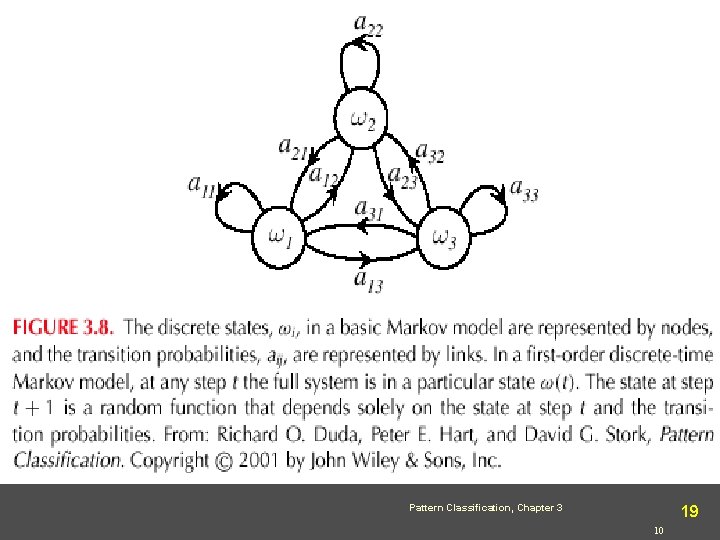
19 Pattern Classification, Chapter 3 19 10

20 = (aij, T) P( T | ) = a 14. a 42. a 21. a 14. P( (1) = i) Example: speech recognition “production of spoken words” Production of the word: “pattern” represented by phonemes /p/ /a/ /tt/ /er/ /n/ // ( // = silent state) Transitions from /p/ to /a/, /a/ to /tt/, /tt/ to er/, /er/ to /n/ and /n/ to a silent state Pattern Classification, Chapter 3 20 10