1 Chapter 25 Data Structures Outline 25 1

1 Chapter 25 – Data Structures Outline 25. 1 Introduction 25. 2 Simple-Type structs, Boxing and Unboxing 25. 3 Self-Referential Classes 25. 4 Linked Lists 25. 5 Stacks 25. 6 Queues 25. 7 Trees 25. 7. 1 Binary Search Tree of Integer Values 25. 7. 2 Binary Search Tree of IComparable Objects Many slides modified by Prof. L. Lilien (even many without an explicit message). 2002 Prentice Hall. All rights reserved. Slides added by L. Lilien are © 2006 Leszek T. Lilien. Permision to use for non-commercial purposes slides added by L. Lilien’s will be gladly granted upon a written (e. g. , emailed) request.

2 25. 1 Introduction • Dynamic data structures – Grow and shrink at execution time – Linked Lists: • “Lined up in a row” • Insertions and removals can occur anywhere in the list – Stacks: • Insertions and removals only at top – Push and pop – Queues: • Insertions made at back, removals from front – Trees, including binary trees: • Facilitate high-speed searching and sorting of data • Efficient elimination of duplicate items 2002 Prentice Hall. All rights reserved.

3 25. 2 Simple-Type structs, Boxing and Unboxing • Data structures can store: – Simple-type values – Reference-type values • There are mechanisms that enable manipulation of simple-type values as objects – Discussed below 2002 Prentice Hall. All rights reserved.

Simple-Type structs • Recall: Each simple type (int, char, …) has a corresponding struct in namespace System that declares this simple type We have structs: – Boolean, Byte, Sbyte, Char, Decimal, Double, Single, Int 32, UInt 32, Int 64, UInt 64, Int 16, UInt 16 • Simple types are just aliases for these corresponding structs – So a variable can be declared: EITHER using the keyword for that simple type OR the struct name • E. g. , int (keyword) and Int 32 (struct name) are interchangeable – Methods related to a simple type are located in the corresponding struct • E. g. method Parse –converting string to int value– is located in struct In 32 2002 Prentice Hall. All rights reserved. 4

Boxing Conversions • All simple-type structs inherit from class Value. Type in namespace System In turn, class Value. Type inherits from class object => Any simple-type value can be assigned to an object variable • Such an assignment is named a Boxing conversions – In Boxing conversion simple-type value is copied into an object => after Boxing conversion , a simple-type value can be manipulated as an object 2002 Prentice Hall. All rights reserved. 5

Boxing Conversions • Boxing conversions can be explicit or implicit int i = 5; // create an int value object obj 1 = ( object) i; // explicitly box the int value object obj 2 = i; // implicitly box the int value – Now obj 1 and obj 2 refer to 2 different objects! • Both objects include a copy of the integer value from the int variable i 2002 Prentice Hall. All rights reserved. 6

Unboxing Conversions 7 • Unboxing conversions — used for explicit conversion of an object reference to a simple value int 1 = ( int ) obj 1; // explicitly unbox the int value // that was boxed within obj 1 • Attempts to unbox an object reference that does not refer to a correct simple value causes Invalid. Cast. Exception • We’ll see later(Ch. 27) how so called “generics” eliminate the overhead of boxing/unboxing 2002 Prentice Hall. All rights reserved.

8 25. 3 Self-Referential Classes • Self-Referential Class – Contains a reference member to an object of the same class type • E. g. : class Node { private int data; private Node next; // self-reference to node … } • Reference can be used to link objects of the same type together • Dynamic data structures require dynamic memory allocation – Ability to obtain memory when needed – Release memory when not needed any more – Uses new operator • Ex: Node node. To. Add = new Node(10); 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Node { private int data; private Node next; // self-reference public Node( int d ) { /* constructor body */ } Reference to object of same type 9 25. 3 Self. Referential Class public int Data { get { /* get body */ } set { } } /* set body */ public Node Next { get { /* get body */ } set { } } } /* set body */ 2002 Prentice Hall. All rights reserved. Fig. 23. 1 Sample self-referential Node class definition (part 1) Slide merged with next by L. Lilien

10 25. 3 Self-Referential Class data 15 next data next 10 Fig. 23. 2 Two self-referential class objects (nodes) linked together. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

11 25. 4 Linked Lists • Linked List: – Linear collection of self-referential nodes connected by links • Nodes: class objects of linked-lists • Programs access linked lists through a reference to first node – Subsequent nodes accessed by link-reference members – Last node’s link set to null to indicate end of list • Nodes can hold data of any type • Nodes created dynamically reference to first node last. Node (with null link) first. Node H 2002 Prentice Hall. All rights reserved. e …… o Slide modified by L. Lilien

12 25. 4 Linked Lists first. Node reference H last. Node refernce D …… Q Fig. 23. 3 A graphical representation of a linked list (with an optional reference to the last node). 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

13 25. 4 Linked Lists • Linked lists - similar to arrays However: • Arrays are a fixed size • Linked lists have no limit to size – More nodes can be added as program executes 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

14 25. 4 Linked Lists - Insert. At. Front first. Node (a) 7 11 new List. Node 12 first. Node (b) 7 11 new List. Node 12 Changed links Unchanged links Fig. 23. 6 A graphical representation of the Insert. At. Front operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

15 25. 4 Linked Lists - Insert. At. Back (a) firt. Node 12 (b) last. Node 7 first. Node 12 11 last. Node 7 Changed links New List. Node 11 5 New List. Node 5 Unchanged links Fig. 23. 7 A graphical representation of the Insert. At. Back operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

16 25. 4 Linked Lists - Remove. From. Front (a) first. Node 12 (b) last. Node 7 11 first. Node 12 5 last. Node 7 11 5 remove. Item Changed links Unchanged links Fig. 23. 8 A graphical representation of the Remove. From. Front operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

17 25. 4 Linked Lists - Remove. From. Back (a) first. Node 12 (b) last. Node 7 11 first. Node 12 5 last. Node 7 11 5 remove. Item Changed links Unchanged links Fig. 23. 9 A graphical representation of the Remove. From. Back operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Outline // Fig. 23. 4: Linked. List. Library. cs // Class List. Node and class List definitions. using System; namespace Linked. List. Library // create library { // class to represent one node in a list class List. Node { Reference to next private object data; // any object can be within a list node private List. Node next; // self-referential memberlist variable List. Node in linked Linked. List. Librar y. cs // constructor to create List. Node that refers to data. Value // and is last node in list (added to the end of the list) public List. Node( object data. Value ) Constructor first item in list : this( data. Value, null ) // calls constructor below { Invoke normal constructor, } which will set data to // constructor to create List. Node that refers to data. Value and next to null // and refers to next List. Node in List (added to any list // position other than the last one) public List. Node( object data. Value, List. Node next. Node ) { Constructor to set data = data. Value; data and next values next = next. Node; } to parameter values // property Next public List. Node Next { get { return next; } 18 Accessor method so a List can access next member variable 2002 Prentice Hall. All rights reserved.

36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 Outline set { next = value; } Linked. List. Librar y. cs } // property Data public object Data { get { return data; } } 19 Accessor method so a List can access data member variable } // end class List. Node Reference to first // class List definition public class List node in list { private List. Node first. Node; private List. Node last. Node; Reference to last private string name; // string like "list" node in listto display // construct empty List with specified name public List( string list. Name ) { name = list. Name; Set reference to first. Node = last. Node = null; and last nodes to null } 2002 Prentice Hall. All rights reserved.

68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 // construct empty List with "list" as its name public List() : this( "list" ) // uses previous constructor { } Outline 20 Linked. List. Librar y. cs // Insert object at front of List. If List is empty, // first. Node and last. Node will refer to same object. // Otherwise, first. Node refers to new node. public void Insert. At. Front( object insert. Item ) { Method to insert an lock ( this ) // ignore-needed in multithreaded environment object at the front of { Get list lock if ( Is. Empty() ) // defined in Line 163 belowthe list first. Node = last. Node = Test if list is empty new List. Node( insert. Item ); else If list is empty, create new first. Node = new List. Node( insert. Item, first. Node ); node and set first. Node and } last. Node to refer to it } If list is not empty, insert // Insert object at end of List. If List is empty, // first. Node and last. Node will refer to same object by setting its next // Otherwise, last. Node's Next property refers to new node. reference to the first node public void Insert. At. Back( object insert. Item ) { Method to insert object into lock ( this ) // ignore-needed in multithreaded environment back of list { Get 163 list below lock if ( Is. Empty() ) // defined in Line first. Node = last. Node = Test if list is empty new List. Node( insert. Item ); If list is empty create a new node and set first. Node and last. Node to reference it 2002 Prentice Hall. All rights reserved.

100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 Outline else last. Node = last. Node. Next = new List. Node( insert. Item ); If list is not empty, create a new node and set the last node’s next Linked. List. Librar reference to the new node y. cs } } // remove first node from List public object Remove. From. Front() { Method to remove an lock ( this ) // ignore-needed in multithreaded environ. from the front of list { object remove. Item = null; object Get lock if ( Is. Empty() ) // defined in Line 163 below Throw throw new Empty. List. Exception( name ) ; exception if list is empy remove. Item = first. Node. Data; // retrieve data // reset first. Node and last. Node references if ( first. Node == last. Node ) first. Node = last. Node = null; else first. Node = first. Node. Next; return remove. Item; } } 21 Set remove. Item equal to data in first node If there is only one node in the list, set first. Node and last. Node references to null // return removed data If there is more then one node, set first. Node to Return data storedreference the second node in node // remove last node from List public object Remove. From. Back() { lock ( this ) // ignore-needed in multithreaded environ. Method to remove an object { from the back of the list object remove. Item = null; 2002 Prentice Hall. All rights reserved.

135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 Outline if ( Is. Empty() ) throw new Empty. List. Exception( name ) ; remove. Item = last. Node. Data; Linked. List. Librar Set remove. Itemy. cs equal to the data in the last node // retrieve data // reset first. Node and last. Node references if ( first. Node == last. Node ) // only one node in list first. Node = last. Node = null; If there is only one node, set first. Node and last. Node to refer to null else { // walk the list until current precedes last. Node List. Node current = first. Node; // loop while current node is not last. Node Loop until next to while ( current. Next != last. Node ) current = current. Next; // move to next node last node is reached // current is now node next to the last // make current new last. Node Set last. Node to refer to last. Node = current; current. Next = null; the next to last node } return remove. Item; } } // return 22 Set reference of new lastdata node to null removed Return data of old last node // return true if List is empty public bool Is. Empty() { Method to test if list is empty lock ( this ) // ignore-needed in multithreaded environment { return first. Node == null; // checks if first. Node == null } } 2002 Prentice Hall. All rights reserved.

170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 // output List contents virtual public void Print() Method to output the list { lock ( this ) // ignore-needed in multithreaded environ. { if ( Is. Empty() ) // defined in Line 163 above { Console. Write. Line( "Empty " + name ); Tell user return; } Outline Linked. List. Librar y. cs if list is empty Console. Write( "The " + name + " is: " ); List. Node current = first. Node; // output current node data while not at end of list while ( current != null ) { Console. Write( current. Data + " " ); current = current. Next; Output } 23 data in list Console. Write. Line( "n" ); } } } // end class List 2002 Prentice Hall. All rights reserved.

199 200 201 202 203 204 205 206 207 208 209 Outline 24 // class Empty. List. Exception definition public class Empty. List. Exception : Application. Exception { public Empty. List. Exception( string name ) Linked. List. Librar Handles illegal operations : base( "The " + name + " is empty" ) { on an empty list y. cs } } // end class Empty. List. Exception } // end namespace Linked. List. Library 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 Outline // Fig 23. 5: List. Test. cs // Testing class List. using System; using Linked. List. Library; List. Test. cs // library we created namespace List. Test { // class to test List class functionality class List. Test { static void Main( string[] args ) { List list = new List(); // create List container // create data to store in List bool a. Boolean = true; char a. Character = '$'; int an. Integer = 34567; string a. String = "hello"; // use List insert methods list. Insert. At. Front( a. Boolean ); list. Print(); list. Insert. At. Front( a. Character ); list. Print(); list. Insert. At. Back( an. Integer ); list. Print(); list. Insert. At. Back( a. String ); list. Print(); // use List remove methods object removed. Object; Create list of objects Create data to put in list Insert objects at beginning of listinto list using Insert. At. Front method Insert objects at end of listinto list using Insert. At. Back method Print the list 2002 Prentice Hall. All rights reserved. 25

35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 // remove data from list and print after each removal try { removed. Object = list. Remove. From. Front(); Console. Write. Line( removed. Object + " removed" ); list. Print(); removed. Object = list. Remove. From. Back(); Console. Write. Line( removed. Object + " removed" ); list. Print(); removed. Object = list. Remove. From. Back (); Console. Write. Line( removed. Object + " removed" ); list. Print(); Outline List. Test. cs Remove objects from front of list using method Remove. From. Front Print the list after each remove Remove objects from back of list using method Remove. From. Back } // process exception if list empty when attempt is // made to remove item catch ( Empty. List. Exception empty. List. Exception ) { Console. Error. Write. Line( "n" + empty. List. Exception ); } If remove is called on an empty list tell user } // end method Main } // end class List. Test } 2002 Prentice Hall. All rights reserved. 26

The list is: True Outline The list is: $ True 34567 List. Test. cs Program Output The list is: $ True 34567 hello $ removed The list is: True 34567 hello True removed The list is: 34567 hello removed The list is: 34567 removed Empty list 2002 Prentice Hall. All rights reserved. 27

We have already seen this and next 3 slides - Review yourself if needed 25. 4 Linked Lists - Insert. At. Front 28 first. Node (a) 7 11 new List. Node 12 first. Node (b) 7 11 new List. Node 12 Changed links Unchanged links Fig. 23. 6 A graphical representation of the Insert. At. Front operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

29 25. 4 Linked Lists - Insert. At. Back (a) firt. Node 12 (b) last. Node 7 first. Node 12 11 last. Node 7 Changed links New List. Node 11 5 New List. Node 5 Unchanged links Fig. 23. 7 A graphical representation of the Insert. At. Back operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

30 25. 4 Linked Lists - Remove. From. Front (a) first. Node 12 (b) last. Node 7 11 first. Node 12 5 last. Node 7 11 5 remove. Item Changed links Unchanged links Fig. 23. 8 A graphical representation of the Remove. From. Front operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

31 25. 4 Linked Lists - Remove. From. Back (a) first. Node 12 (b) last. Node 7 11 first. Node 12 5 last. Node 7 11 5 remove. Item Changed links Unchanged links Fig. 23. 9 A graphical representation of the Remove. From. Back operation. 2002 Prentice Hall. All rights reserved. Slide modified by L. Lilien

32 25. 5 Stacks • Stack – a special version of a linked list: – Last-in, first-out (LIFO) data structure: • Takes and releases new nodes only at top • Operations: – Push: adds new entry (node) to top of stack – Pop: removes top entry (node) from stack • Can be used for: – Storing return addresses – Storing local variables – … 2002 Prentice Hall. All rights reserved.

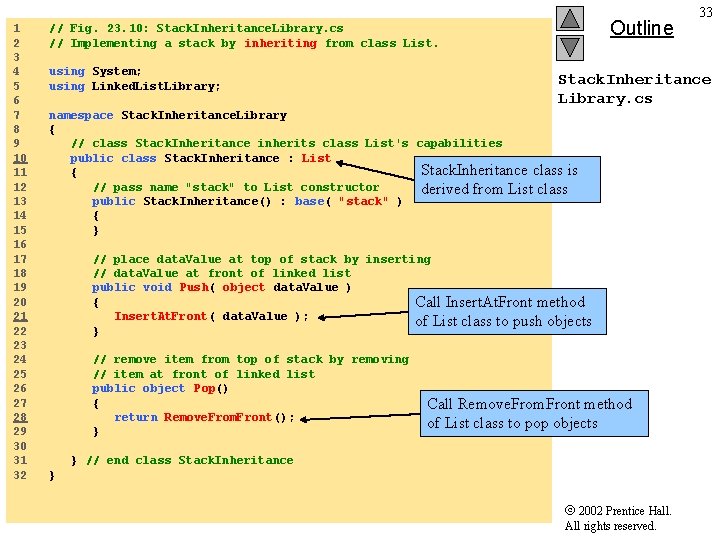
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Outline // Fig. 23. 10: Stack. Inheritance. Library. cs // Implementing a stack by inheriting from class List. using System; using Linked. List. Library; Stack. Inheritance Library. cs namespace Stack. Inheritance. Library { // class Stack. Inheritance inherits class List's capabilities public class Stack. Inheritance : List Stack. Inheritance class is { // pass name "stack" to List constructor derived from List class public Stack. Inheritance() : base( "stack" ) { } // place data. Value at top of stack by inserting // data. Value at front of linked list public void Push( object data. Value ) { Call Insert. At. Front method Insert. At. Front( data. Value ); of List class to push objects } // remove item from top of stack by removing // item at front of linked list public object Pop() { return Remove. From. Front(); } 33 Call Remove. From. Front method of List class to pop objects } // end class Stack. Inheritance } 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Outline // Fig. 23. 11: Stack. Inheritance. Test. cs // Testing class Stack. Inheritance. using System; using Stack. Inheritance. Library; using Linked. List. Library; Stack. Inheritance Test. cs namespace Stack. Inheritance. Test { // demonstrate functionality of class Stack. Inheritance. Test { static void Main( string[] args ) { Stack. Inheritance stack = new Stack. Inheritance(); // create objects to store in the stack bool a. Boolean = true; char a. Character = '$'; Create objects int an. Integer = 34567; store in stack string a. String = "hello"; // use method Push to add items to stack. Push( a. Boolean ); stack. Print(); stack. Push( a. Character ); stack. Print(); stack. Push( an. Integer ); stack. Print(); stack. Push( a. String ); stack. Print(); 34 Create stack to Push objects onto the stack Print stack after each push // use method Pop to remove items from stack object removed. Object = null; 2002 Prentice Hall. All rights reserved.

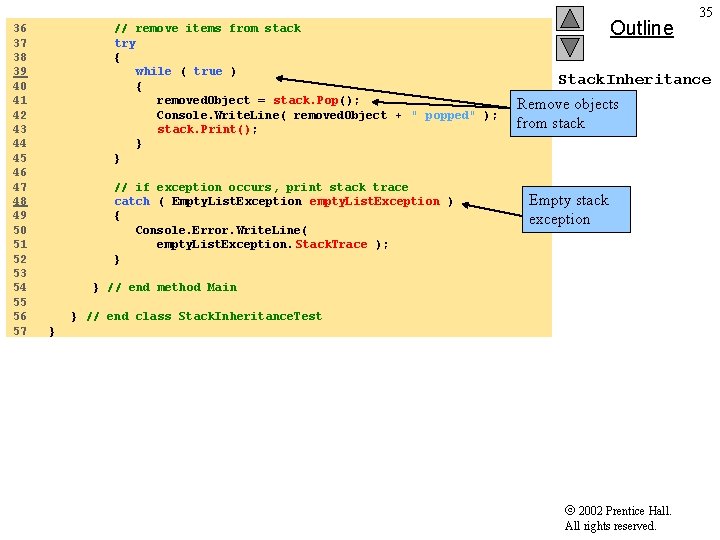
36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 // remove items from stack try { while ( true ) { removed. Object = stack. Pop(); Console. Write. Line( removed. Object + " popped" ); stack. Print(); } } // if exception occurs, print stack trace catch ( Empty. List. Exception empty. List. Exception ) { Console. Error. Write. Line( empty. List. Exception. Stack. Trace ); } Outline 35 Stack. Inheritance Test. cs Remove objects from stack Empty stack exception } // end method Main } // end class Stack. Inheritance. Test } 2002 Prentice Hall. All rights reserved.

The stack is: True Outline 36 The stack is: $ True The stack is: 34567 $ True The stack is: hello 34567 $ True Stack. Inheritance Test. cs Program Output hello popped The stack is: 34567 $ True 34567 popped The stack is: $ True $ popped The stack is: True popped Empty stack at Linked. List. Library. List. Remove. From. Front() in z: ch 24linkedlistlibrary. cs: line 114 at Stack. Inheritance. Library. Stack. Inheritance. Pop() in z: ch 24stackinheritancelibrary stackinheritancelibrary. cs: line 28 at Stack. Inheritance. Test. Main(String[] args in z: ch 24fig 24_11stackinheritancetest. cs: line 41 Line 144 - Slide 16 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 // Fig. 23. 12: Stack. Composition. Library. cs // Stack. Composition definition with composed List object. // (no inheritance here!) using System; using Linked. List. Library; Outline Stack. Composition Library. cs namespace Stack. Composition. Library { // class Stack. Composition encapsulates List's capabilities public class Stack. Composition { Create List object private List stack; // construct empty stack public Stack. Composition() { stack = new List( "stack" ); } // add object to stack public void Push( object data. Value ) { stack. Insert. At. Front( data. Value ); } // remove object from stack public object Pop() { return stack. Remove. From. Front(); } 37 Call method Insert. At. Front to push Use method Remove. From. Front to pop 2002 Prentice Hall. All rights reserved.

32 33 34 35 36 37 38 39 40 41 42 43 44 45 // determine whether stack is empty public bool Is. Empty() { return stack. Is. Empty(); Call } is empty to see if list has nodes // output stack contents public void Print() { stack. Print(); } Outline 38 Stack. Composition Library. cs Call method Print for output } // end class Stack. Composition } 2002 Prentice Hall. All rights reserved.

39 25. 6 Queues • Queue: First-in, first-out (FIFO) data structure – Nodes added to tail, removed from head • Operations: – Enqueue: insert node at the end – Dequeue: remove node from the front • Many computer applications: – Printer spooling – Information packets on networks – … 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Outline // Fig. 23. 13: Queue. Inheritance. Library. cs // Implementing a queue by inheriting from class List. using System; using Linked. List. Library; 40 Queue. Inheritance Library. cs namespace Queue. Inheritance. Library { // class Queue. Inheritance inherits List's capabilities public class Queue. Inheritance : List { Class Queue. Inheritance // pass name "queue" to List constructor public Queue. Inheritance() : base( "queue" ) derives from class List { } // place data. Value at end of queue by inserting // data. Value at end of linked list public void Enqueue( object data. Value ) Call Insert. At. Back { Insert. At. Back( data. Value ); to enqueue } // remove item front of queue by removing // item at front of linked list public object Dequeue( ) { return Remove. From. Front(); Call Remove. From. Front } to dequeue } // end of Queue. Inheritance } 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Outline // Fig. 23. 14: Queue. Test. cs // Testing class Queue. Inheritance. using System; using Queue. Inheritance. Library; using Linked. List. Library; Queue. Test. cs namespace Queue. Test { // demonstrate functionality of class Queue. Inheritance class Queue. Test { static void Main( string[] args ) { Queue. Inheritance queue = new Queue. Inheritance(); // create objects to store in the stack bool a. Boolean = true; char a. Character = '$'; int an. Integer = 34567; string a. String = "hello"; Create queue Create objects to be inserted into queue // use method Enqueue to add items to queue. Enqueue( a. Boolean ); queue. Print(); Enqueue objects queue. Enqueue( a. Character ); queue. Print(); queue. Enqueue( an. Integer ); Print queue after queue. Print(); each enqueue. Enqueue( a. String ); queue. Print(); // use method Dequeue to remove items from queue object removed. Object = null; 2002 Prentice Hall. All rights reserved. 41

36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 // remove items from queue try { while ( true ) { removed. Object = queue. Dequeue(); Console. Write. Line( removed. Object + " dequeue" ); queue. Print(); } Print queue after } Outline Queue. Test. cs Dequeue objects each enqueue // if exception occurs, print stack trace catch ( Empty. List. Exception empty. List. Exception ) { Console. Error. Write. Line( empty. List. Exception. Stack. Trace ); } } // end method Main } // end class Queue. Test } 2002 Prentice Hall. All rights reserved. 42

The queue is: True Outline The queue is: True $ 34567 Queue. Test. cs Program Output The queue is: True $ 34567 hello True dequeue The queue is: $ 34567 hello $ dequeue The queue is: 34567 hello 34567 dequeue The queue is: hello dequeue Empty queue at Linked. List. Library. List. Remove. From. Front() in z: ch 24linkedlistlibrary. cs: line 114 at Queue. Inheritance. Library. Queue. Inheritance. Dequeue() in z: ch 24queueinheritancelibrary queueinheritancelibrary. cs: line 28 at Queue. Test. Main(String[] args) in z: ch 24fig 24_13queuetest. cs: line 41 2002 Prentice Hall. All rights reserved. 43

44 25. 7 Trees • Tree: non-linear, two-dimensional data structure • Binary tree: – Each node contains data & two links (hence “binary in the name): left link and right link B – Root node: “top” node in a tree • Links refer to child nodes – Leaf node: node with no children X A Y 2002 Prentice Hall. All rights reserved.

45 25. 7 Trees • Binary search tree: – Values in left subtree are less than the value of the subtree’s parent – Values in right subtree are greater than the value of the subtree’s parent 47 J A 25 P 11 M 2002 Prentice Hall. All rights reserved. 77 43 65 93

46 25. 7. 1 Binary Search Tree of Integer Values • Traversal: method of retrieving data from a tree – In these methods if there is a subtree, recursively the traversal is called recursively • Kinds of traversals: – Inorder traversal: • Get data from left subtree/child of node • Get data from right subtree/child of node 25 • Example (figure) Inorder traversal: 11 25 43 47 65 77 93 2002 Prentice Hall. All rights reserved. 47 11 77 43 65 93

25. 7. 1 Binary Search Tree of Integer Values – Preorder traversal: • • 25 11 Get data from node Get data from left subtree/child of node Get data from right subtree/child of node Example: 47 25 11 43 77 65 93 77 43 – Postorder traversal • • Get data from left subtree/child of node Get data from right subtree/child of node Get data from node Example: 11 43 25 65 93 77 47 – Level-order traversal • Visit nodes of tree row by row, from left to right • Example: 47 25 77 11 43 65 93 2002 Prentice Hall. All rights reserved. 47 47 65 93

48 25. 7 Trees Reference to the tree B A D C Fig. 23. 15 A graphical representation of a binary tree. 2002 Prentice Hall. All rights reserved.

49 25. 7 Trees 47 25 77 11 7 43 17 31 65 44 93 68 Fig. 23. 16 A binary search tree containing 12 values. 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Outline // Fig. 23. 17: Binary. Tree. Library. cs // Definition of class Tree. Node and class Tree. using System; namespace Binary. Tree. Library { // class Tree. Node definition class Tree. Node { private Tree. Node left. Node; private int data; private Tree. Node right. Node; Binary. Tree. Librar y. cs Left and right subtree references Data stored in node // initialize data and make this a leaf node public Tree. Node( int node. Data ) { data = node. Data; left. Node = right. Node = null; // node has no children } // Left. Node property public Tree. Node Left. Node { get { return left. Node; } Since new nodes are leaf, set subtree references to null Accessor methods for left subtree set { left. Node = value; } } 50 2002 Prentice Hall. All rights reserved.

36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 // Data property public int Data { get { return data; } Outline Accessor methods for nodes data Binary. Tree. Librar y. cs set { data = value; } } // Right. Node property public Tree. Node Right. Node { get { return right. Node; } 51 Accessor methods for right subtree set { right. Node = value; } } 2002 Prentice Hall. All rights reserved.

65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 Outline 52 // insert Tree. Node into Binary Search Tree containing nodes; // ignore duplicate values public void Insert( int insert. Value ) Method to determine { location of new Binary. Tree. Librar node // insert in left subtree y. cs if ( insert. Value < data ) { // insert new Tree. Node If value of new node is less than if ( left. Node == null ) root, and the left subtree is empty, left. Node = new Tree. Node( insert. Value ); insert node as left child of root // continue traversing left subtree else left. Node. Insert( insert. Value ); } // insert in right subtree else if ( insert. Value > data ) { // insert new Tree. Node if ( right. Node == null ) right. Node = new Tree. Node( insert. Value ); If left subtree is not empty, recursively call Insert to determine location of new node in subtree // continue traversing right subtree else right. Node. Insert( insert. Value ); } } } // ignore if insert. Value == data (duplicate value) // end method Insert // end class Tree. Node If value of new node is greater than root, and the right subtree is empty, insert node as right child of root If right subtree is not empty, recursively call Insert to determine location of new node in subtree 2002 Prentice Hall. All rights reserved.

97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 // class Tree definition public class Tree { private Tree. Node root; Outline Reference to root of tree Binary. Tree. Librar y. cs // construct an empty Tree of integers public Tree() { Set root to null when root = null; } tree first created // Insert a new node in the binary search tree. // If the root node is null, create the root node here. // Otherwise, call the insert method of class Tree. Node. public void Insert. Node( int insert. Value ) Method to insert a { lock ( this ) // ignore locks new node into tree { if ( root == null ) root = new Tree. Node( insert. Value ); If tree is empty insert new node as root else root. Insert( insert. Value ); // see l. 67 } } // begin preorder traversal public void Preorder. Traversal() { lock ( this ) { Preorder. Helper( root ); } } 53 If tree is not empty call Insert to determine location of new node Perform preorder traversal Call Preorder. Helper to help perform traversal 2002 Prentice Hall. All rights reserved.

132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 // recursive method to perform preorder traversal private void Preorder. Helper( Tree. Node node ) { if ( node == null ) return; // output data from this node Console. Write( node. Data + " " ); // traverse left subtree Preorder. Helper( node. Left. Node ); // traverse right subtree Preorder. Helper( node. Right. Node ); } // begin inorder traversal public void Inorder. Traversal() { lock ( this ) { Inorder. Helper( root ); } } Method to help with Binary. Tree. Librar preorder traversal y. cs Display node data Call Preorder. Helper recursively on left subtree Call Preorder. Helper recursively on right subtree Perform inorder traversal Call Inorder. Helper to help with traversal // recursive method to perform inorder traversal private void Inorder. Helper( Tree. Node node ) { if ( node == null ) return; // traverse left subtree Inorder. Helper( node. Left. Node ); Outline 54 Method to help with inorder traversal Call Inorder. Helper recursively on left subtree 2002 Prentice Hall. All rights reserved.

166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 // output node data Console. Write( node. Data + " " ); // traverse right subtree Inorder. Helper( node. Right. Node ); } // begin postorder traversal public void Postorder. Traversal() { lock ( this ) { Postorder. Helper( root ); } } Call Inorder. Helper Binary. Tree. Librar recursively on righty. cs subtree Perform postorder traversal Call Postorder. Helper to help with traversal // recursive method to perform postorder traversal private void Postorder. Helper( Tree. Node node ) { if ( node == null ) return; // traverse left subtree Postorder. Helper( node. Left. Node ); // traverse right subtree Postorder. Helper( node. Right. Node ); // output node data Console. Write( node. Data + " " ); } } } Outline Display node data 55 Method to help with postorder traversal Call Postorder. Helper recursively on left subtree Call Postorder. Helper recursively on right subtree Display node data // end class Tree 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Outline // Fig. 23. 18: Tree. Test. cs // This program tests class Tree. using System; using Binary. Tree. Library; namespace Tree. Test { // class Tree. Test definition public class Tree. Test { // test class Tree static void Main( string[] args ) { Tree tree = new Tree(); int insert. Value; Tree. Test. cs Create a tree Console. Write. Line( "Inserting values: " ); Random random = new Random(); // insert 10 random integers from 0 -99 in tree for ( int i = 1; i <= 10; i++ ) { insert. Value = random. Next( 100 ); Console. Write( insert. Value + " " ); Insert ten nodes in tree. Insert. Node( insert. Value ); } // perform preorder traveral of tree Console. Write. Line( "nn. Preorder traversal" ); tree. Preorder. Traversal(); Call preorder traversal 2002 Prentice Hall. All rights reserved. 56

34 35 36 37 38 39 40 41 42 43 44 45 // perform inorder traveral of tree Console. Write. Line( "nn. Inorder traversal" ); tree. Inorder. Traversal(); // perform postorder traveral of tree Console. Write. Line( "nn. Postorder traversal" ); tree. Postorder. Traversal(); Console. Write. Line(); Outline Call inorder traversal Tree. Test. cs Call postorder traversal } } // end class Tree. Test } Inserting values: 39 69 94 47 50 72 55 41 97 73 Program Output Preorder traversal 39 69 47 41 50 55 94 72 73 97 Inorder traversal 39 41 47 50 55 69 72 73 94 97 Postorder traversal 41 55 50 47 73 72 97 94 69 39 2002 Prentice Hall. All rights reserved. 57

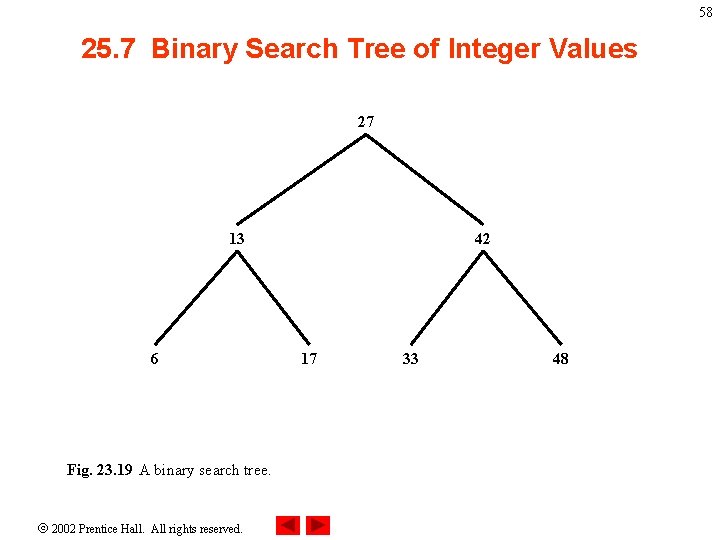
58 25. 7 Binary Search Tree of Integer Values 27 13 6 Fig. 23. 19 A binary search tree. 2002 Prentice Hall. All rights reserved. 42 17 33 48

59 25. 7. 2 Binary Search Tree of IComparable Objects • Can use polymorphism to manipulate objects of different types in uniform ways – Binary search trees can be implemented to manipulate data of any object that implements the IComparable interface • Implementation of IComparable defines: – Compare. To method • E. g. : public void Insert( IComparable insert. Value ) { … if ( insert. Value. Compare. To( data ) < 0 ) … } – insert. Value. Compare. To( data ) returns value: • < 0 if insert. Value < data • = 0 if they are equal • > 0 if insert. Value > data 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 // Fig. 23. 20: Binary. Tree. Library 2. cs // Definition of class Tree. Node and class Tree for IComparable // objects. using System; Outline Binary. Tree. Librar y 2. cs namespace Binary. Tree. Library 2 { // class Tree. Node definition class Tree. Node { private Tree. Node left. Node; private IComparable data; // polymorphic data stored in node private Tree. Node right. Node; // initialize data and make this a leaf node public Tree. Node( IComparable node. Data ) { data = node. Data; left. Node = right. Node = null; // node has no children } // Left. Node property public Tree. Node Left. Node { get { return left. Node; } set { left. Node = value; } } 60 2002 Prentice Hall. All rights reserved.

36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 // Data property public IComparable Data { get { return data; } Outline 61 Binary. Tree. Librar y 2. cs set { data = value; } } // Right. Node property public Tree. Node Right. Node { get { return right. Node; } set { right. Node = value; } } 2002 Prentice Hall. All rights reserved.

65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 Outline 62 // insert Tree. Node into Tree that contains nodes; // ignore duplicate values public void Insert( IComparable insert. Value ) { // insert. Value of polymorphic-enabling type IComparable Binary. Tree. Librar // insert in left subtree y 2. cs if ( insert. Value. Compare. To( data ) < 0 ) // Use need. Icomparable’s method { // ‘insert. Value < data’ not sufficient – cf. sl. 47 l. 70) Compare. To to determine if new // insert new Tree. Node if ( left. Node == null ) node is less than its parent left. Node = new Tree. Node( insert. Value ); // continue traversing left subtree else left. Node. Insert( insert. Value ); // recursive } // insert in right subtree Use Icomparable’s method else if ( insert. Value. Compare. To( data ) > 0 ) Compare. To to determine if new {// ‘insert. Value > data’ not sufficient – cf. sl. 47 l. 82 // insert new Tree. Node node is greater than its parent if ( right. Node == null ) right. Node = new Tree. Node( insert. Value ); // continue traversing right subtree else right. Node. Insert( insert. Value ); // recursive } // ignore if insert. Value. Compare. To( data ) == 0 (duplicate value) } // end method Insert } // end class Tree. Node 2002 Prentice Hall. All rights reserved.

97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 // class Tree definition public class Tree // differences w. r. t. Fig. 23. 17 { private Tree. Node root; in red // construct an empty Tree of integers public Tree() { root = null; } Outline Binary. Tree. Librar y 2. cs // Insert a new node in the binary search tree. // If the root node is null, create the root node here. // Otherwise, call the insert method of class Tree. Node. public void Insert. Node( IComparable insert. Value ) { lock ( this ) { if ( root == null ) root = new Tree. Node( insert. Value ); } } else root. Insert( insert. Value ); // use Insert from // previous slide to insert new node into tree // rooted at ‘root’ // begin preorder traversal public void Preorder. Traversal() { lock ( this ) { Preorder. Helper( root ); } } 63 2002 Prentice Hall. All rights reserved.

132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 // recursive method to perform preorder traversal private void Preorder. Helper( Tree. Node node ) { if ( node == null ) return; Outline 64 Binary. Tree. Librar y 2. cs // output node data Console. Write( node. Data + " " ); // traverse left subtree Preorder. Helper( node. Left. Node ); // traverse right subtree Preorder. Helper( node. Right. Node ); } // begin inorder traversal public void Inorder. Traversal() { lock ( this ) { Inorder. Helper( root ); } } // recursive method to perform inorder traversal private void Inorder. Helper( Tree. Node node ) { if ( node == null ) return; // traverse left subtree Inorder. Helper( node. Left. Node ); 2002 Prentice Hall. All rights reserved.

166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 // output node data Console. Write( node. Data + " " ); // traverse right subtree Inorder. Helper( node. Right. Node ); } Outline Binary. Tree. Librar y 2. cs // begin postorder traversal public void Postorder. Traversal() { lock ( this ) { Postorder. Helper( root ); } } // recursive method to perform postorder traversal private void Postorder. Helper( Tree. Node node ) { if ( node == null ) return; // traverse left subtree Postorder. Helper( node. Left. Node ); // traverse right subtree Postorder. Helper( node. Right. Node ); // output node data Console. Write( node. Data + " " ); } } } 65 // end class Tree 2002 Prentice Hall. All rights reserved.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Outline // Fig. 23. 21: Tree. Test. cs // This program tests class Tree. using System; using Binary. Tree. Library 2; namespace Tree. Test { // class Tree. Test definition public class Tree. Test { // test class Tree static void Main( string[] args ) { int[] int. Array = { 8, 2, 4, 3, 1, 7, 5, 6 }; double[] double. Array = { 8. 8, 2. 2, 4. 4, 3. 3, 1. 1, 7. 7, 5. 5, 6. 6 }; string[] string. Array = { "eight", "two", "four", "three", "one", "seven", "five", "six" }; Tree. Test. cs Populate trees with int, double and string values // create int Tree // - using: public class Tree int. Tree = new Tree(); // empty tree populate. Tree( int. Array, int. Tree, "int. Tree" ); // next sl. traverse. Tree( int. Tree, "int. Tree" ); // next sl. // create double Tree double. Tree = new Tree(); populate. Tree( double. Array, double. Tree, "double. Tree" ); traverse. Tree( double. Tree, "double. Tree" ); // create string Tree string. Tree = new Tree(); populate. Tree( string. Array, string. Tree, "string. Tree" ); traverse. Tree( string. Tree, "string. Tree" ); } 2002 Prentice Hall. All rights reserved. 66

36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 Outline // populate Tree with array elements static void populate. Tree( Method to add data Array array, Tree tree, string name ) from arrays to trees Tree. Test. cs { Console. Write. Line( "n. Inserting into " + name + ": " ); foreach ( IComparable data in array ) { Console. Write( data + " " ); tree. Insert. Node( data ); } Insert nodes into tree } // insert perform traversals static void traverse. Tree( Tree tree, string tree. Type ) { // perform preorder traveral of tree Console. Write. Line( "nn. Preorder traversal of " + tree. Type ); tree. Preorder. Traversal(); // perform inorder traveral of tree Console. Write. Line( "nn. Inorder traversal of " + tree. Type ); tree. Inorder. Traversal(); Method to traverse tree Perform preorder traversal Perform inorder traversal 2002 Prentice Hall. All rights reserved. 67

63 64 65 66 67 68 69 70 71 // perform postorder traveral of tree Console. Write. Line( "nn. Postorder traversal of " + tree. Type ); tree. Postorder. Traversal(); Console. Write. Line( "n" ); } } Outline Tree. Test. cs Perform postorder traversal // end class Tree. Test } Inserting into int. Tree: 8 2 4 3 1 7 5 6 Program Output Preorder traversal of int. Tree 8 2 1 4 3 7 5 6 Inorder traversal of int. Tree 1 2 3 4 5 6 7 8 Postorder traversal of int. Tree 1 3 6 5 7 4 2 8 2002 Prentice Hall. All rights reserved. 68

Inserting into double. Tree: Outline 8. 8 2. 2 4. 4 3. 3 1. 1 7. 7 5. 5 6. 6 Preorder traversal of double. Tree 8. 8 2. 2 1. 1 4. 4 3. 3 7. 7 5. 5 6. 6 Tree. Test. cs Program Output Inorder traversal of double. Tree 1. 1 2. 2 3. 3 4. 4 5. 5 6. 6 7. 7 8. 8 Postorder traversal of double. Tree 1. 1 3. 3 6. 6 5. 5 7. 7 4. 4 2. 2 8. 8 Inserting into string. Tree: eight two four three one seven five six Preorder traversal of string. Tree eight two four five three one seven six Inorder traversal of string. Tree eight five four one seven six three two Postorder traversal of string. Tree five six seven one three four two eight 2002 Prentice Hall. All rights reserved. 69

70 The End 2002 Prentice Hall. All rights reserved.