1 CHAPTER 16 RATIONAL DATABASE DESIGN ALGORITHMS AND

1 CHAPTER 16 RATIONAL DATABASE DESIGN ALGORITHMS AND FURTHER DEPENDENCIES ~リレーショナルデータベース設計アルゴリズムとさらなる依存関係 教育輪講 2014/5/14 B 4 moe

2 INTRODUCTION • Chapter 15: top-down設計 • relational design by analysis(分解) • Chapter 16: bottom-up設計 • relational design by synthesis(統合)






8 Fの閉包(closure) • F = {Ssn → {Ename, Bdate, Address, Dnumber} Dnumber → 感覚的に理解できるが {Dname, Dmgr_ssn} } 6つの推論規則に基づく Fから推測できる関数従属性は • Ssn → {Dname, Dmgr_ssn} • Ssn → Ssn • Dnumber → Dname





17 アルゴリズムの使用例 • F = {Ssn → Ename, Pnumber → {Pname, Plocation}, {Ssn, Pnumber} → Hours} アルゴリズムの使用 • {Ssn} + : = {Ssn}; 繰り返し Ssn → Ename:{Ssn} ⊆ {Ssn}+ なので {Ssn} + : = {Ssn} ∪ {Ename} = {Ssn, Ename } • {Ssn} + = {Ssn, Ename} • {Pnumber} + = {Pnumber, Pname, Plocation} • {Ssn, Pnumber} += {Ssn, Pnumber, Ename, Plocation, Hours}






24 正規形の分解と不全 n universal relation schema(普遍関係スキーマ) データベースの全ての属性を含む R = {A 1, A 2, . . . , An} n universal relation assumption(普遍関係仮定) すべての属性名が一意である n attribute preservation (属性保存) D:universal relation schema Rの分解 D= {R 1, R 2, . . . , Rm}








32 無損失結合性 Nonadditive (Lossless) Join Property 例:




37 第 3正規形での従属性保存分解 (Dependency-Preserving Decomposition into 3 NF Schemas) アルゴリズム 16. 4の例: • U(Emp_ssn, Pno, Esal, Ephone, Dno, Pname, Plocation) • FD 1: Emp_ssn → {Esal, Ephone, Dno} • FD 2: Pno → { Pname, Plocation} • FD 3: Emp_ssn, Pno → {Esal, Ephone, Dno, Pname, Plocation} 極小被覆を求める(Algorithm 16. 2) • Minimal cover G: {Emp_ssn → Esal, Ephone, Dno; Pno → Pname, Plocation}



40 ボイスコッド正規形での無損失結合分解 (Nonadditive Join Decomposition into BCNF Schemas) 例 Student Course Instructor Course Narayan Database Mark Database Smith Database Navathe Database Smith Operating Systems Ammar Operating Systems Smith Theory Schulman Theory Wallace Database Mark Ahamad Operating Systems Wallace Operating Systems Ahamad Omiecinski Database Wong Database Omiecinski Student Instructor Zelaya Database Navathe Narayan Mark Narayan Operating Systems Ammar Smith Navathe Smith Ammar Smith Schulman Wallace Mark Wallace Ahamad Wong Omiecinski Zelaya Navathe Narayan Ammar Q={Student, Course, Instructor} BCNFに違反するX → Y X: Instructor → Y: Course リレーションスキーマ(Q – Y) と(X ∪ Y) Q−Y:{Student, Instructor} X ∪ Y : {Instructor, Course}



43 3 NFでの従属性保存分解と無損失結合分解 (Dependency-Preserving and Nonadditive Join Decomposition into 3 NF) 例1:step 3使用例 • U(Emp_ssn, Pno, Esal, Ephone, Dno, Pname, Plocation) FD 1: Emp_ssn → {Esal, Ephone, Dno} FD 2: Pno → { Pname, Plocation} FD 3: Emp_ssn, Pno → {Esal, Ephone, Dno, Pname, Plocation} • R 1 (Emp_ssn, Esal, Ephone, Dno) • R 2 (Pno, Pname, Plocation) • R 3 (Emp_ssn, Pno) ←new!

44 3 NFでの従属性保存分解と無損失結合分解 (Dependency-Preserving and Nonadditive Join Decomposition into 3 NF) 例2:Case X FD 1: Property_id → Lot#, County, Area FD 2: Lot#, County → Area, Property_id FD 3: Area → County 極小被覆を求める(Algorithm 16. 2) F : { P → LCA, LC → AP, A → C }. F : {P → L, P → C, P → A, LC → P, A → C}. Minimal cover GX: {P → LC, LC → AP, A → C } Step 2 Design X: R 1 (P, L, C), R 2 (L, C, A, P), and R 3 (A, C) Step 4 R 3はR2の射影、R1はR2の射影なのでR1、R3は削除 すべてを満たす 3 NFスキーマは Design X: R 2 (L, C, A, P)

45 3 NFでの従属性保存分解と無損失結合分解 (Dependency-Preserving and Nonadditive Join Decomposition into 3 NF) 例3:Case Y FD 1: Property_id → Lot#, County, Area FD 2: Lot#, County → Area, Property_id FD 3: Area → County 極小被覆を求める(Algorithm 16. 2) F : { P → LCA, LC → AP, A → C }. F : {P → C, P → A, P → L, LC → A, LC → P, A → C}. Minimal cover GY: {P → LA, LC → P, A → C } Step 2 Design X Design Y: S 1 (P, A, L), S 2 (L, C, P), and S 3 (A, C) Step 4 すべてのFDは元の関係と同じで不要な物がない S1、S3はBCNF設計⇒S2は不必要 S2はS1、S3の射影なので削除できない NULL値発生の可能性 Design Yは 16. 6でおき得る1つの結果

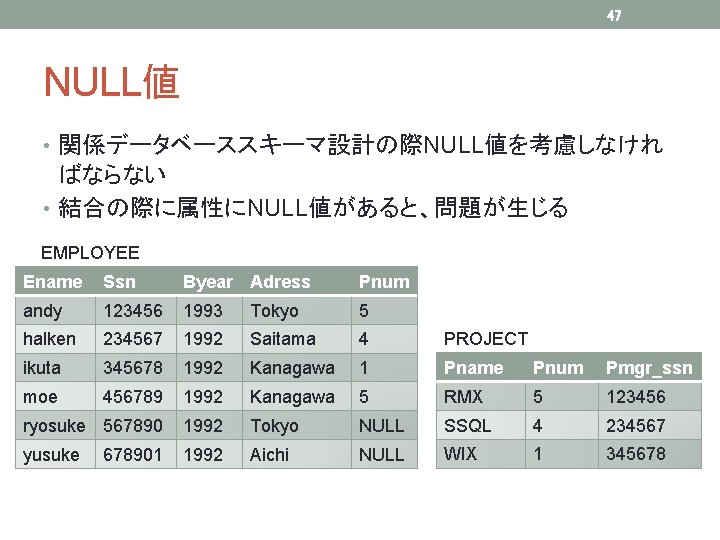
47 NULL値 • 関係データベーススキーマ設計の際NULL値を考慮しなけれ ばならない • 結合の際に属性にNULL値があると、問題が生じる EMPLOYEE Ename Ssn Byear Adress Pnum andy 123456 1993 Tokyo 5 halken 234567 1992 Saitama 4 PROJECT ikuta 345678 1992 Kanagawa 1 Pname Pnum Pmgr_ssn moe 456789 1992 Kanagawa 5 RMX 5 123456 ryosuke 567890 1992 Tokyo NULL SSQL 4 234567 yusuke 1992 Aichi NULL WIX 1 345678 678901
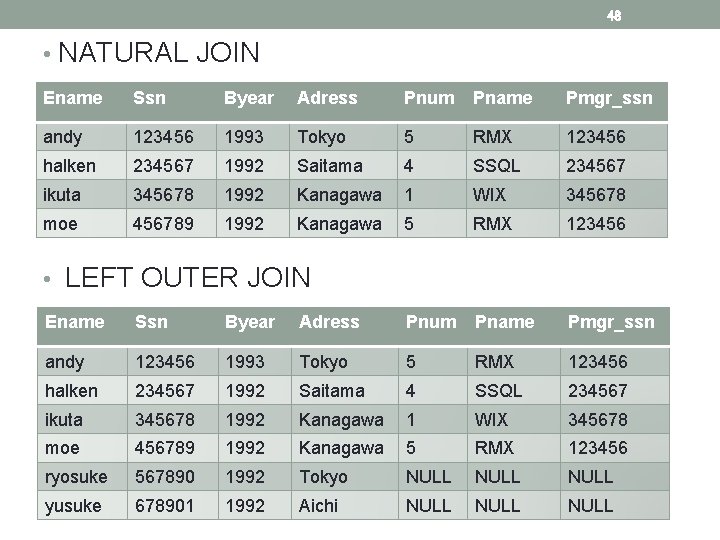
48 • NATURAL JOIN Ename Ssn Byear Adress Pnum Pname Pmgr_ssn andy 123456 1993 Tokyo 5 RMX 123456 halken 234567 1992 Saitama 4 SSQL 234567 ikuta 345678 1992 Kanagawa 1 WIX 345678 moe 456789 1992 Kanagawa 5 RMX 123456 • LEFT OUTER JOIN Ename Ssn Byear Adress Pnum Pname Pmgr_ssn andy 123456 1993 Tokyo 5 RMX 123456 halken 234567 1992 Saitama 4 SSQL 234567 ikuta 345678 1992 Kanagawa 1 WIX 345678 moe 456789 1992 Kanagawa 5 RMX 123456 ryosuke 567890 1992 Tokyo NULL yusuke 678901 1992 Aichi NULL
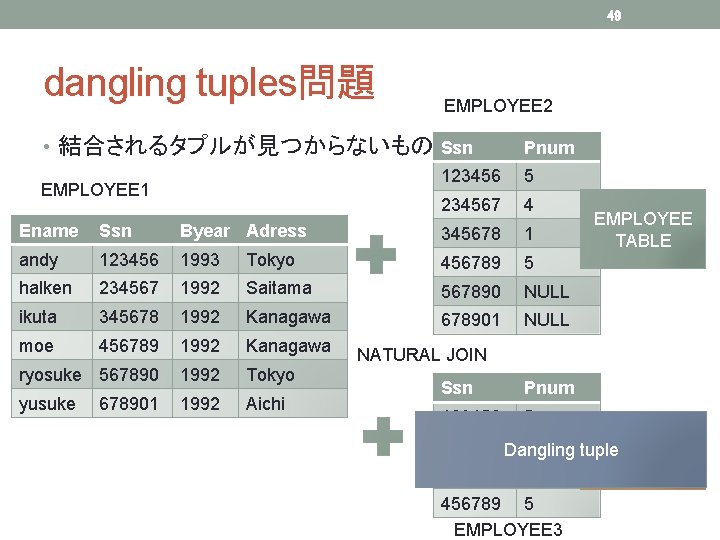
49 dangling tuples問題 EMPLOYEE 2 • 結合されるタプルが見つからないもの Ssn EMPLOYEE 1 Pnum 123456 5 234567 4 Ename Ssn Byear Adress 345678 1 andy 123456 1993 Tokyo 456789 5 halken 234567 1992 Saitama 567890 NULL ikuta 345678 1992 Kanagawa 678901 NULL moe 456789 1992 Kanagawa ryosuke 567890 1992 Tokyo yusuke 1992 Aichi 678901 EMPLOYEE TABLE NATURAL JOIN Ssn Pnum 123456 5 ryosuke 234567 Dangling 4 tuple yusuke 345678 1 456789 5 EMPLOYEE 3




53 多値の依存関係の推論規則 MVDのみ IR4 補完律(complementation rule) : {X →→ Y} |= {X →→ (R – (X ∪ Y))} • IR 5 増加律(augmentation rule) :If X →→ Y and W ⊇ Z, then WX →→ YZ • IR 6 推移律(transitive rule) : {X →→ Y, Y →→ Z} |= X →→ (Z – Y) • IR 7 複製律(replication rule for FD to MVD) : {X → Y} |= X→→ Y • IR 8 合体律(coalescence rule for FDs and MVDs) : If X →→ Y and there exists W with the properties that (a) W ∩ Y is empty, (b) W → Z, and, (c) Y ⊇ Z, MVD, FD then X → Z. •



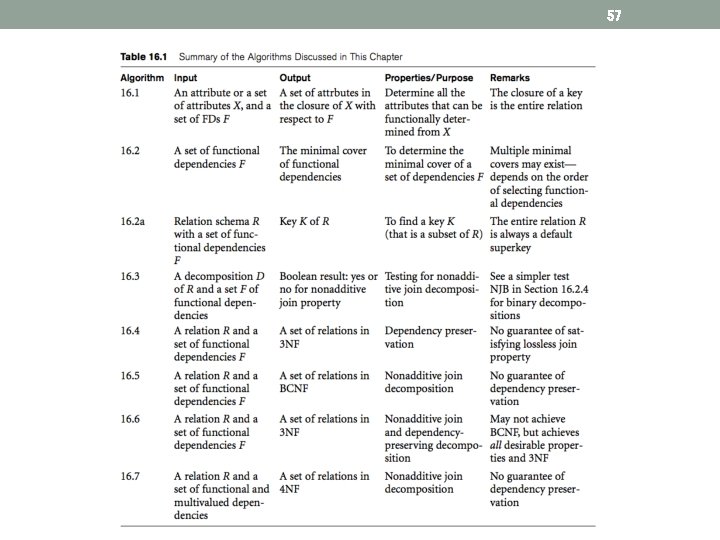
57



60 包含従属性(Inclusion Dependencies) 包含従属性 • 参照整合性制約(Referential integrity constraints)を表す。 • クラスやサブクラスの関係を表すのに使用される 包含従属性の例 • EMPLOYEE. Ssn < PERSON. Ssn • ALUMNUS. Ssn < PERSON. Ssn • STUDENT. Ssn < PERSON. Ssn



63 テンプレート従属性(Template Dependencies) 例: (a)FD X→Y X={A, B} Y={C, D} (b)MDV X→→Y X={A, B} Y={C} (c)Include dependency R. X < S. Y X={C, D} Y={E, F}


65 算術関数の関数従属 (FD Based on Arithmetic Functions and Procedures) 例: 関係 ORDER_LINE (Order, Item, Quantity, Unit_price, Extended_price) 式で表すと • Extended_price = Unit_price * Quantity. • (Quantity, Unit_price ) → Extended_price


- Slides: 63