1 C Venn Diagrams and Subsets The Universe

§ 1. C Venn Diagrams and Subsets

The Universe of Discourse and the Universal Set Recall that a set is a collection of objects. We would like to find a graphical way to describe various sets and their relationships. We may be dealing with several sets that draw from a common pool of objects. Such a collection of objects is called the universe of discourse for the sets whose compositions come from this pool of elements. Examples: Ø If we are considering sets of automobiles, a universe of discourse could be all motorized vehicles Ø If we are considering sets of cosmological objects, a universe of discourse could be the cosmos

The Universe of Discourse and the Universal Set (Continued) The mathematical study of sets is called Set Theory. The universe of discourse is called the universal set in Set Theory. The universal set is: Ø a set whose elements are a pool containing all the elements of sets that are under study Ø dependent on the context of sets that are under study Ø is not the “set of all sets” in the context of the sets under study

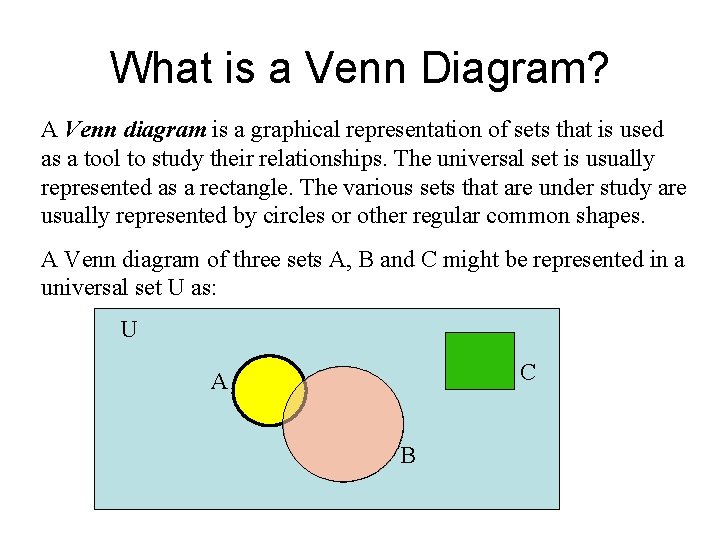
What is a Venn Diagram? A Venn diagram is a graphical representation of sets that is used as a tool to study their relationships. The universal set is usually represented as a rectangle. The various sets that are under study are usually represented by circles or other regular common shapes. A Venn diagram of three sets A, B and C might be represented in a universal set U as: U C A B

Venn Diagrams (Continued) The following observations hold for the diagram: Ø All the elements of the sets A, B and C are elements of U Ø Sets A and B are composed of elements some of which are common to both Ø Set C has no elements in common with either set A or set B

The Complement of a Set Consider a set A as a subset of a universal set U. Then the complement of A is the subset of U consisting of all the elements of U that are not also elements of A. We write the complement of A as A’, where A’ = U – A. A A’ = U – A U

The Compliment of a Set Let A be a set in the context of a universal set U. The compliment of the set A is a set A' defined as follows: A' ={x | x ϵ U, but x ϵ/ A} The Venn diagram for A' is U A' A where A' is the light blue are of the diagram.

What is a Subset? Let A be a set. A set B is a subset of A if every element of B is an element of A. We write this mathematically as B A. The symbol ‘ ’ means “is contained in or equal to”. In terms of a Venn diagram: U A A B B The set A is a subset of itself, i. e. , A A. . The empty set is a subset of every set, i. e. ø A.

Equal Sets and Proper Subsets of Sets Let A and B be two sets. We say that A and B are equal, written A = B, if B A and A B. A set B is a proper subset of a set A if B A and there is a least one element of A that is not an element of B. When B is a proper subset of A we write B A.

De Morgan’s Laws for Sets Given that A and B are subsets of the same universal set U. Then ∩ Ø(A ∩ Ø (A ∩ B)’ = A’ B’ B)’ = A’ ∩ B’ These two relations are called De Morgan’s Laws for sets.

How Many Subsets are there in a Finite Set of n Elements? We will explicitly list all the subsets for a set of 3 elements. Let A = {a, b, c}. Then the following are all the subsets of A: ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} We see that there are 8 subsets of A. Note that 8 = 23. We can now use inductive reasoning to suppose that if A is a finite set with n elements, we can construct 2 n subsets from the elements of A. This is indeed the case.