1 Booth encoding n What is Booth Encoding


1. Booth encoding n What is Booth Encoding ? n Modified Booth Encoding n Sign Extension-compensation vector n Original Multiplier Structure

2. Power Dissipation n Transition probability n MSD Property n Proposed Multiplier Structure

What is Booth Encoding ? n Y = -2 n-1 yn-1 + 2 n-2 yn-2+…+20 y 0 = -2 n-1(yn-2 - yn-1 ) + 2 n-2(yn-3 -yn-2) +……+20(y 1 –y 0)

Modified Booth Encoding n Y = -2 n-1 yn-1 + 2 n-2 yn-2+…+20 y 0 = 2 n-2(2 yn-1 - 2 yn – yn-1 + yn-2) +…… + 20(-2 y 1+y 0) = 2 n-2(- 2 yn + yn-1 + yn-2 ) +……
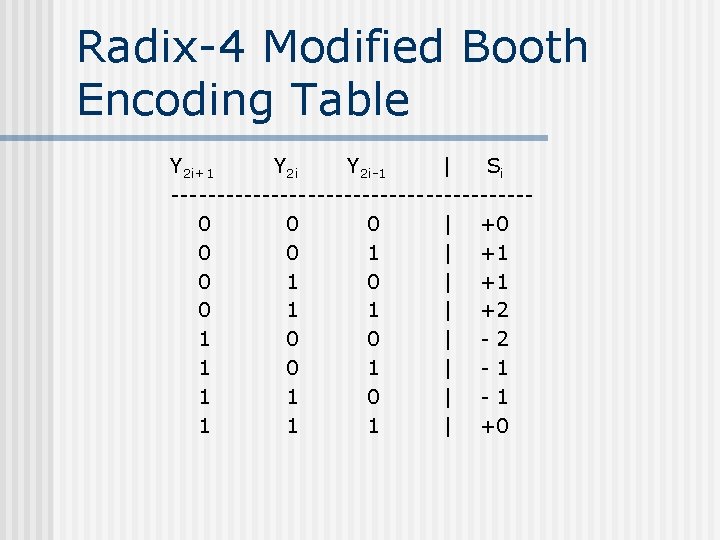
Radix-4 Modified Booth Encoding Table Y 2 i+1 Y 2 i-1 | Si --------------------0 0 0 | +0 0 0 1 | +1 0 1 1 | +2 1 0 0 | -2 1 0 1 | -1 1 1 0 | -1 1 | +0
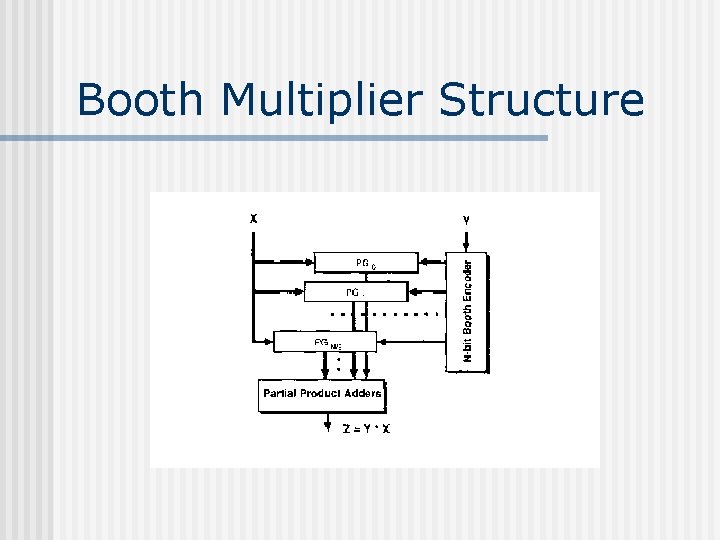
Booth Multiplier Structure

Sign-generate Sign extension
Correction Factor

Example

Reduced Transitions

Encoding Operation
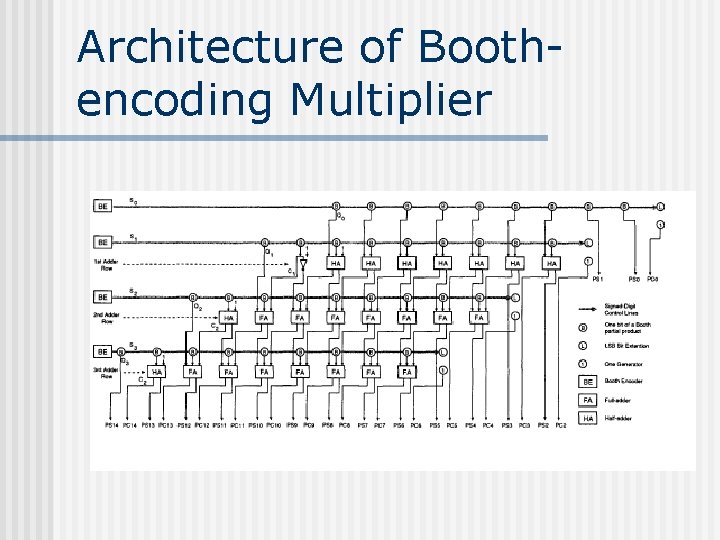
Architecture of Boothencoding Multiplier

The Power Dissipation n Power = 0. 5 CLVDD 2 f. CLKESW : The switching activity =>The probability of a transition within a clock cycle

Transition probability PΔ(s) = 2 p(s)(1 -p(s)) p(s)=probability of s being nonzero Transition: May cause glitches in combinatorial circuits=> High switch probability->Short logic depth n

The One Probability of A Carry Signal n P(C 1) = p(Qm)p(Qn) Qm, Qn are the two partial-products added in the first adder row

Carry output of k-th adder row n P(Ck) = 0. 5 p(Ck-1) + 0. 5 p(Qi) Ck : a carry out of the k-th adder row Qi : a partial product added into the k-th adder row (P(CARRY)=p 1 p 2+p 2 p 3+p 3 p 1 -2 p 1 p 2 p 3 when p 1=0. 5)

MSD For a signal that has a smaller magnitude than its wordlength n 000…. xxxxx…. n 111…. xxxxx…. n Repeat sign-extension bits n Booth encoding (Si) as +0 n

A Signal Property n n n P(Qi) = p(X)p(Si) p(X)=0. 5 for random multiplicand The MSD has low p(Si) and hence low p(Qi) P(Qi)<0. 5, P(Qi) implies PΔ(Qi) Fist add the MSD partial-product in a carry-save array for reduced switching
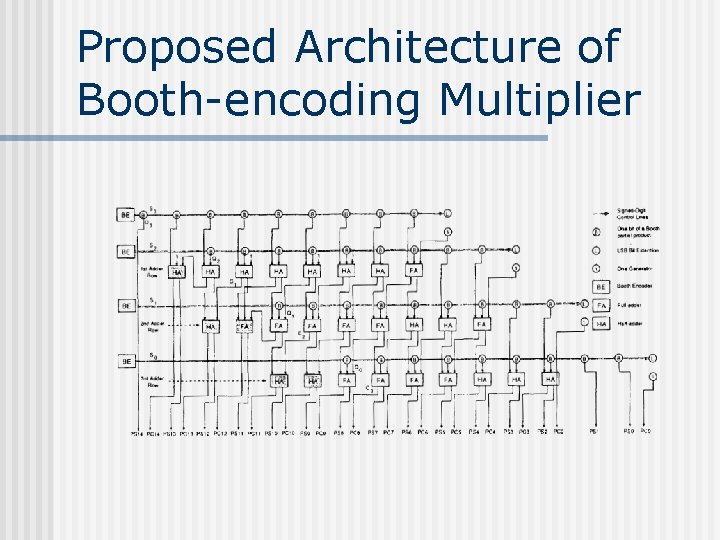
Proposed Architecture of Booth-encoding Multiplier
- Slides: 20