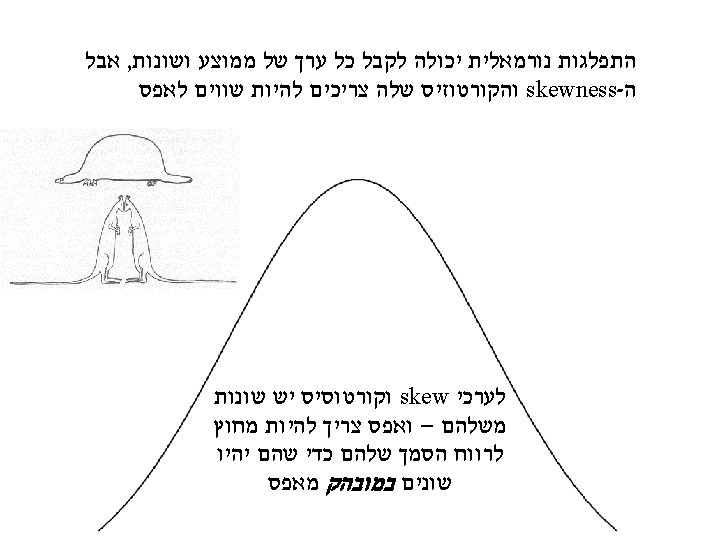
1 Arithmetic mean xin Geometric mean x 1x






















![t-test in R t. test(x, y) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) males<-size[Sex=="male"] females<-size[Sex=="female"] t-test in R t. test(x, y) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) males<-size[Sex=="male"] females<-size[Sex=="female"]](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-29.jpg)


![ANOVA in R aov model<-aov(x~y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" "what" ANOVA in R aov model<-aov(x~y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" "what"](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-32.jpg)
![correlation in R cor. test(x, y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" correlation in R cor. test(x, y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species"](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-34.jpg)

















































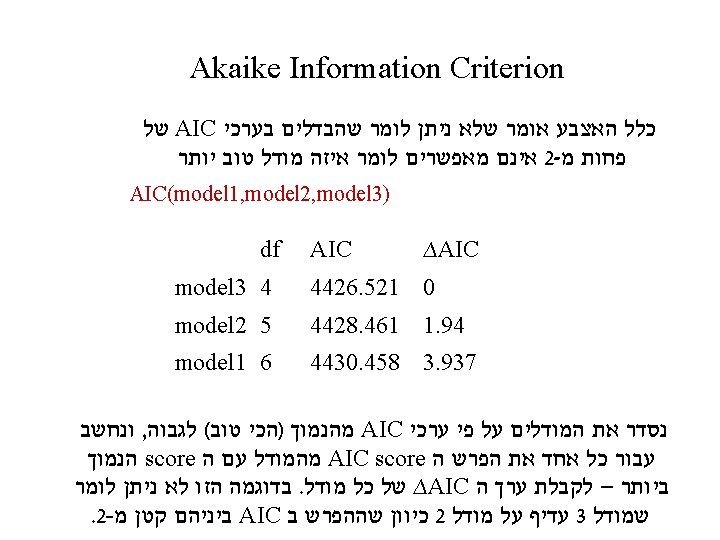

![Model selection: variation on the AIC theme AICc = AIC+(2 k*[k+1]/[n-k-1]) AICc. 1 עבור Model selection: variation on the AIC theme AICc = AIC+(2 k*[k+1]/[n-k-1]) AICc. 1 עבור](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-103.jpg)

- Slides: 104



* מדדים לנטייה מרכזית ממוצע. 1 הרמוני , גיאומטרי , חשבוני Arithmetic mean: Σxi/n Geometric mean: (x 1*x 2*…*xn)1/n Harmonic mean: * = Moments of central tendency

R- מדדים לנטייה מרכזית ב Arithmetic mean: Σxi/n : דוגמא ממוצע חשבוני. 1 “mean” הפונקציה data<-c(2, 3, 4, 5, 6, 7, 8) mean(data) [1] 5 Geometric mean: (x 1*x 2*…*xn)1/n ממוצע גיאומטרי. 2 : דוגמא : ניתן גם לעבוד מהקובץ dat<-read. csv("island_type_final 2. csv") Attach(dat) mean(lat) [1] 17. 40439 data<-c(2, 3, 4, 5, 6, 7, 8) exp(mean(log(data))) [1] 4. 549163

* מדדים לנטייה מרכזית (mean) ממוצע. א. 1 (median) חציון. ב (mode) שכיח. ג * = Moments of central tendency : דוגמא מהקובץ median(mass) [1] 0. 69 data<-c(2, 3, 4, 5, 6, 7, 8) median(data) [1] 5



מדדים לנטייה מרכזית #for: data<-c(2, 3, 4, 5, 6, 7, 8) length(data) var(data) : גודל מדגם : שונות sd(data) : סטיית תקן se<-(sd(data)/length(data)^0. 5) se [1] 0. 8164966 : שגיאת תקן CV<-sd(data)/mean(data) CV [1] 0. 4320494 : coefficient of variation


מדדים לנטייה מרכזית (Skew) הטייה skew<-function(data){ m 3<-sum((data-mean(data))^3)/length(data) s 3<-sqrt(var(data))^3 m 3/s 3} skew(data) sdskew<-function(x) sqrt(6/length(x)) : שגיאת תקן של הטיה


מדדים לנטייה מרכזית (Kurtosis) קורטוזיס. 1 kurtosis<-function(x){ m 4<-sum((x-mean(x))^4)/length(x) s 4<-var(x)^2 m 4/s 4 -3 } kurtosis(x) sdkurtosis<-function(x) sqrt(24/length(x)) : שגיאת תקן של קורטוזיס




Residuals כשאנחנו עושים סטטיסטיקה אנחנו יוצרים מודלים של המציאות dat<-read. csv("island_type_final 2. csv") model<-lm(mass~iso+area+age+lat, data=dat) out<-model$residuals out write. table(out, file = "residuals. txt", sep="t", col. names=F, row. names=F) #note that residual values are in the order entered (i. e. , not alphabetic, not by residual size – first in, first out) Residual = ₪ 37428 Residual = 33 cm Residual = -23 month service


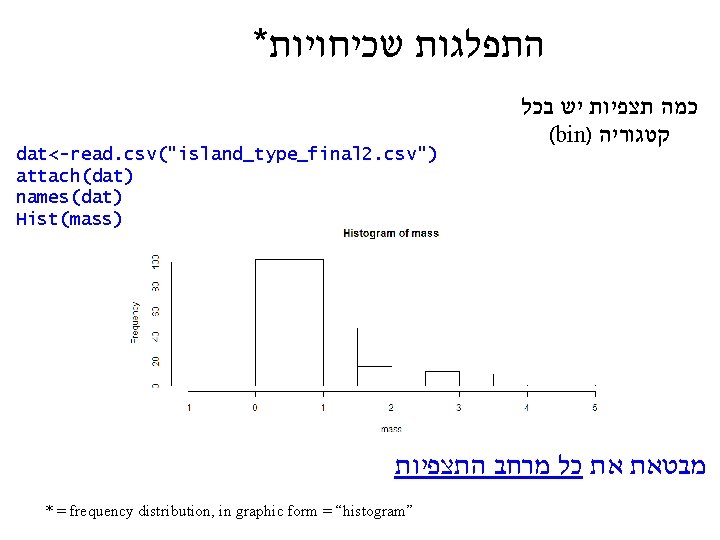
* התפלגות שכיחויות dat<-read. csv("island_type_final 2. csv") attach(dat) names(dat) Hist(mass) כמה תצפיות יש בכל (bin) קטגוריה מבטאת את כל מרחב התצפיות * = frequency distribution, in graphic form = “histogram”


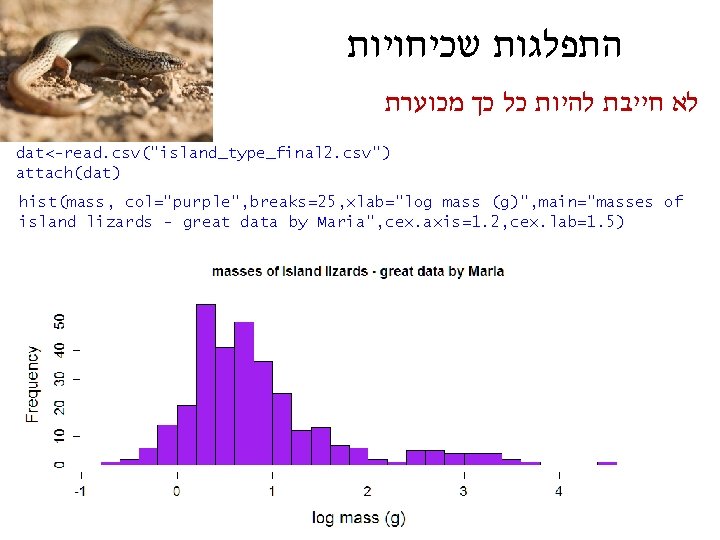
התפלגות שכיחויות לא חייבת להיות כל כך מכוערת dat<-read. csv("island_type_final 2. csv") attach(dat) hist(mass, col="purple", breaks=25, xlab="log mass (g)", main="masses of island lizards - great data by Maria", cex. axis=1. 2, cex. lab=1. 5)

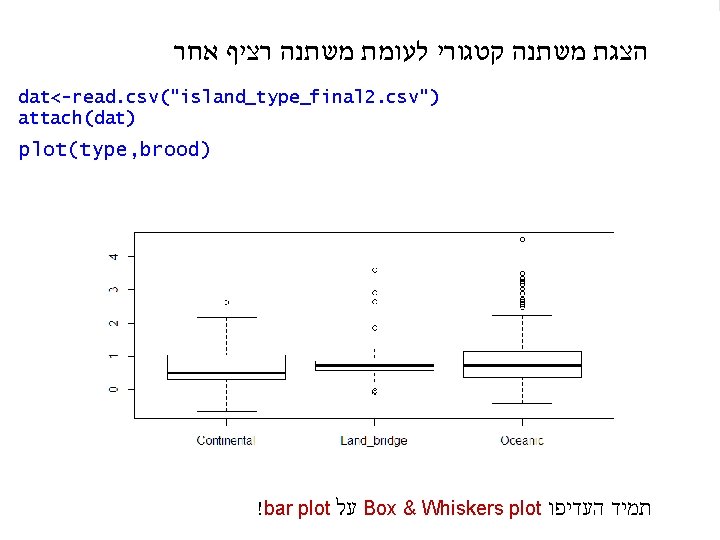
הצגת משתנה קטגורי לעומת משתנה רציף אחר dat<-read. csv("island_type_final 2. csv") attach(dat) plot(type, brood) !bar plot על Box & Whiskers plot תמיד העדיפו

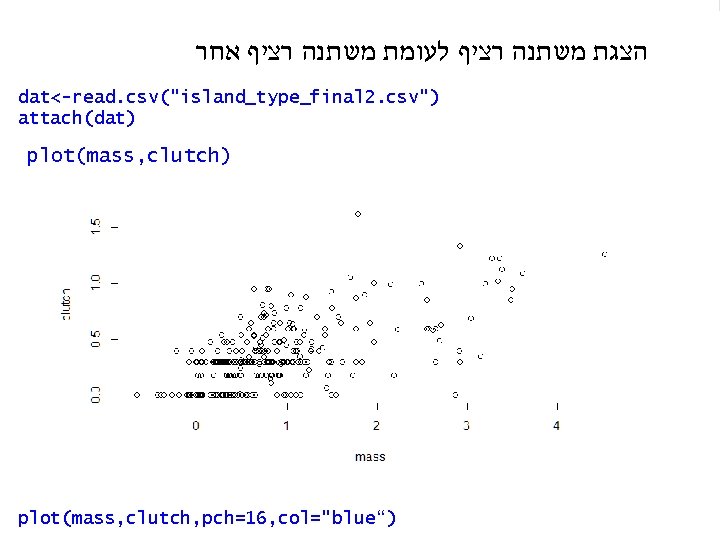
הצגת משתנה רציף לעומת משתנה רציף אחר dat<-read. csv("island_type_final 2. csv") attach(dat) plot(mass, clutch, pch=16, col="blue“)



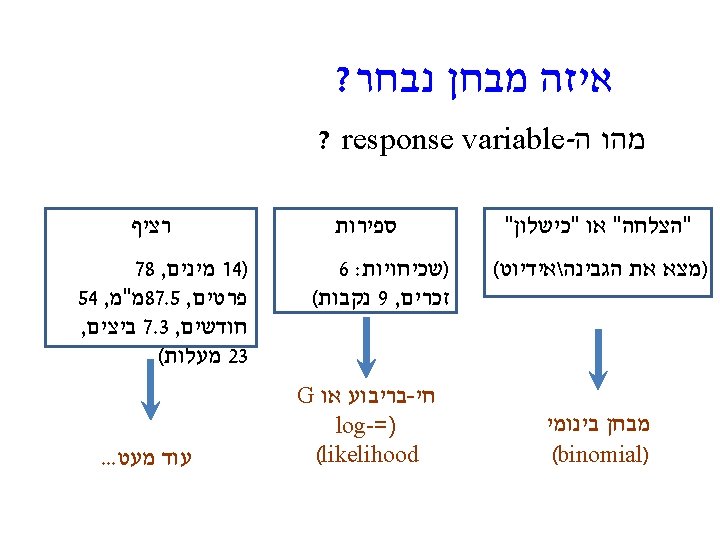
Binomial test in R. יש להגדיר את מספר ההצלחות מתוך גודל המדגם הכולל 20 מתוך 19 : 2 דוגמה binom. test(19, 34) . ( )לא מובהק 34 מתוך 19 : 1 דוגמה ( )מובהק Exact binomial test data: 19 and 34 number of successes = 19, number of trials = 34 p-value = 0. 6076 alternative hypothesis: true probability of success is not equal to 0. 5 95 percent confidence interval: 0. 3788576 0. 7281498 sample estimates: probability of success 0. 5588235 binom. test(19, 20) Exact binomial test data: 19 and 20 number of successes = 19, number of trials = 20, p-value = 4. 005 e-05 alternative hypothesis: true probability of success is not equal to 0. 5 95 percent confidence interval: 0. 7512672 0. 9987349 sample estimates: probability of success 0. 95

Chi-square test in R Data: lizard insularity & diet: chisq. test habitat island mainland M<-as. table(rbind(c(1901, 101, 269), c(488, 43, 177))) chisq. test(M) data: M χ2 = 80. 04, df = 2, p-value < 2. 2 e-16 diet carnivore herbivore omnivore species# 488 43 177 1901 101 269

Chi-square test in R chisq. test : והפעם עם בסיס הנתונים שלנו dat<-read. csv("island_type_final 2. csv") type anoles else install. packages("reshape") Continental 7 45 Library(reshape) Land_bridge 1 30 cast(dat, type ~ what, length) Oceanic M<-as. table(rbind(c(7, 45), c(1, 30, 14), c(23, 110, 44))) chisq. test(M) data: M χ2 = 17. 568, df = 4, p-value = 0. 0015 23 110 gecko 45 14 44

![ttest in R t testx y dimorphismread csvssd csv headerT attachdimorphism namesdimorphism malessizeSexmale femalessizeSexfemale t-test in R t. test(x, y) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) males<-size[Sex=="male"] females<-size[Sex=="female"]](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-29.jpg)
t-test in R t. test(x, y) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) males<-size[Sex=="male"] females<-size[Sex=="female"] t. test(females, males) Sex female male female male female size 79. 7 85 120 133. 0 118 126. 0 105. 8 112 106 121. 0 95 111. 0 86 93. 0 65 75. 0 230 240. 0 Welch Two Sample t-test data: females and males t = -2. 1541, df = 6866. 57, p-value = 0. 03127 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 7. 5095545 -0. 3536548 sample estimates: mean of x mean of y 88. 17030 92. 10191

t-test in R (2) Sex female male female male female lm(x~y) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) model<-lm(size~Sex, data=dimorphism) summary(model) (Intercept) Sexmale Estimate 88. 17 3. 932 standard error 1. 291 1. 825 t 68. 32 2. 154 p value <2 e-16 *** 0. 031 * size 79. 7 85 120 133. 0 118 126. 0 105. 8 112 106 121. 0 95 111. 0 86 93. 0 65 75. 0 230 240. 0

Species Xenagama_zonura Xenosaurus_grandis Xenosaurus_newmanorum Xenosaurus_penai Xenosaurus_platyceps Xenosaurus_rectocollaris Zonosaurus_anelanelany Zootoca_vivipara Zygaspis_nigra Zygaspis_quadrifrons Paired t-test in R t. test(x, y, paired=TRUE) dimorphism<-read. csv("ssd. csv", header=T) attach(dimorphism) names(dimorphism) males<-size[Sex=="male"] females<-size[Sex=="female"] t. test(females, paired=TRUE) size 79. 7 85 120 133. 0 118 126. 0 105. 8 112 106 121. 0 95 111. 0 86 93. 0 65 75. 0 230 240. 0 195 227. 0 Sex female male female male female Paired t-test data: females and males t = -10. 192, df = 3503, p-value < 2. 2 e-16 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -4. 688 -3. 175 sample estimates: mean of the differences -3. 931 tapply(size, Sex, mean) female 88. 17 male 92. 10
![ANOVA in R aov modelaovxy islandread csvislandtypefinal 2 csv headerT namesisland 1 species what ANOVA in R aov model<-aov(x~y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" "what"](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-32.jpg)
ANOVA in R aov model<-aov(x~y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" "what" "family" "insular" "Archipelago" "largest_island" [7] "area" "type" "age" "iso" "lat" "mass" [13] "clutch" "brood" "hatchling" "productivity“ model<-aov(clutch~type, data=island) summary(model) Df type 2 Residuals 289 species Trachylepis_sechellensis Trachylepis_wrightii Tropidoscincus_boreus Tropidoscincus_variabilis Urocotyledon_inexpectata Varanus_beccarii Algyroides_fitzingeri Anolis_wattsi Archaeolacerta_bedriagae Cnemaspis_affinis Cnemaspis_limi Cnemaspis_monachorum Amblyrhynchus_cristatus Ameiva_erythrocephala Ameiva_fuscata Ameiva_plei Anolis_acutus Anolis_aeneus Anolis_agassizi Anolis_bimaculatus Anolis_bonairensis Sum sq Mean sq F value Pr(>F) 0. 466 0. 23296 2. 784 0. 0635. 24. 184 0. 08368 type Continental Continental Land_bridge Land_bridge Oceanic Oceanic Oceanic clutch 0. 65 0. 45 0. 3 0. 58 0. 4 0 0. 65 0. 3 0. 18 0 0. 35 0. 6 0. 41 0 0. 18 0

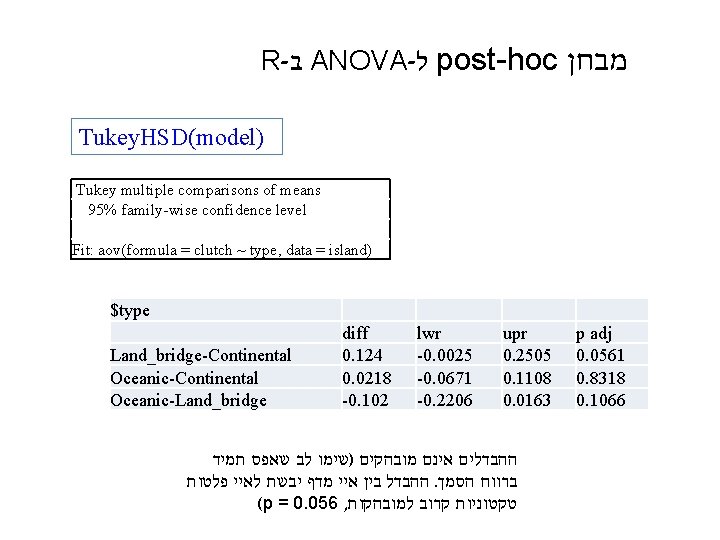
R- ב ANOVA- ל post-hoc מבחן Tukey. HSD(model) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = clutch ~ type, data = island) $type Land_bridge-Continental Oceanic-Land_bridge diff 0. 124 0. 0218 -0. 102 lwr -0. 0025 -0. 0671 -0. 2206 upr 0. 2505 0. 1108 0. 0163 ההבדלים אינם מובהקים )שימו לב שאפס תמיד ההבדל בין איי מדף יבשת לאיי פלטות. ברווח הסמך (p = 0. 056 , טקטוניות קרוב למובהקות p adj 0. 0561 0. 8318 0. 1066
![correlation in R cor testx y islandread csvislandtypefinal 2 csv headerT namesisland 1 species correlation in R cor. test(x, y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species"](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-34.jpg)
correlation in R cor. test(x, y) island<-read. csv("island_type_final 2. csv", header=T) names(island) [1] "species" "what" "family" "insular" "Archipelago" "largest_island" [7] "area" "type" "age" "iso" "lat" "mass" [13] "clutch" "brood" "hatchling" "productivity“ attach(island) cor. test(mass, lat) Pearson's product-moment correlation data: mass and lat t = -1. 138, df = 317, p-value = 0. 256 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0. 17239 0. 04635 sample estimates: cor -0. 06378 r “ הוא מקדם הקורלציה cor” המשתנה lat 5 5 4 18 18 18 20 18 18 18 5 21 21 21 22 21 mass 1. 21 0. 83 1. 84 1. 39 0. 42 0. 29 0. 45 1. 54 0. 36 0. 27 0. 04 0. 01 1. 21 0. 95 0. 51 0. 29 0. 74 0. 92

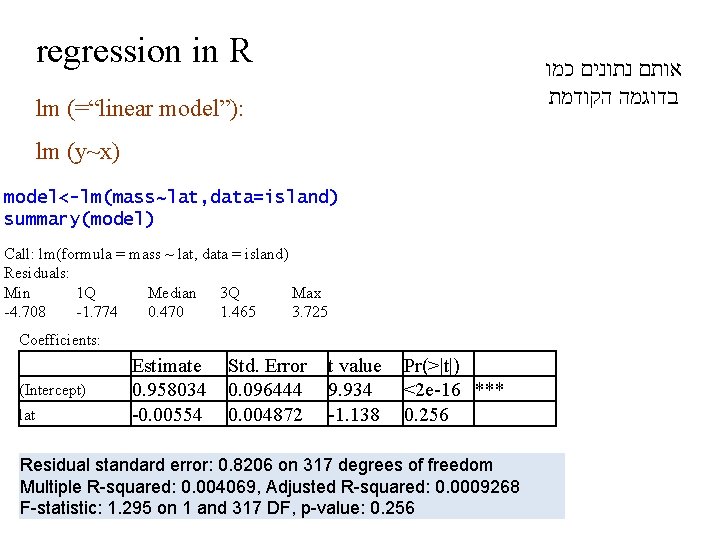
regression in R אותם נתונים כמו בדוגמה הקודמת lm (=“linear model”): lm (y~x) model<-lm(mass~lat, data=island) summary(model) Call: lm(formula = mass ~ lat, data = island) Residuals: Min 1 Q Median 3 Q Max -4. 708 -1. 774 0. 470 1. 465 3. 725 Coefficients: (Intercept) lat Estimate 0. 958034 -0. 00554 Std. Error 0. 096444 0. 004872 t value 9. 934 -1. 138 Pr(>|t|) <2 e-16 *** 0. 256 Residual standard error: 0. 8206 on 317 degrees of freedom Multiple R-squared: 0. 004069, Adjusted R-squared: 0. 0009268 F-statistic: 1. 295 on 1 and 317 DF, p-value: 0. 256


lm לעומת aov. lm גם במבחן ANOVA- אולי במפתיע אפשר לבחון נתונים המתאימים ל (! כולל )חשוב , במבחן רגרסיה lm של summary- במקרה כזה נקבל את כל המידע שנותן ה 2 לכל קונטרסט )בין p- הבדלים בין פקטורים וערכי , שגיאות תקן , parameter estimates ( קטגוריות של המשתנה המסביר הקטגוריאלי island<-read. csv("island_type_final 2. csv", header=T) model<-aov(clutch~type, data=island) model 2<-lm(clutch~type, data=island) summary(model 2) Df type 2 Residuals 289 (Intercept) type. Land_bridge type. Oceanic Sum sq Mean sq F value Pr(>F) 0. 466 0. 23296 2. 784 0. 0635. 24. 184 0. 08368 Estimate 0. 33149 0. 12399 0. 02184 Std. Error 0. 02984 0. 05369 0. 03777 t value 11. 11 2. 309 0. 578 Residual standard error: 0. 2893 on 289 degrees of freedom (27 observations deleted due to missingness) Multiple R-squared: 0. 0189, Adjusted R-squared: 0. 01211 F-statistic: 2. 784 on 2 and 289 DF, p-value: 0. 06346 aov טבלת Pr(>|t|) <2 e-16 0. 0216 0. 5635 *** * עוד בהמשך lm טבלת


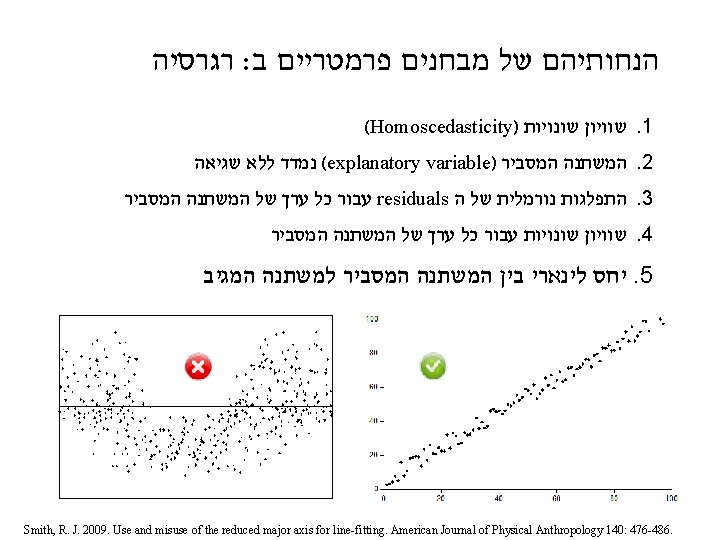
ANOVA. הנחותיהם של מבחנים פרמטריים א בנוסף להנחות של כל מבחן (Homoscedasticity) שיוויון שוניות. 1 residuals- התפלגות נורמלית של ה. 2 "Comments on earlier drafts of this manuscript made it clear that for many readers who analyze data but who are not particularly interested in statistical questions, any discussion of statistical methods becomes uncomfortable when the term ‘‘error variance’’ is introduced. “ Smith, R. J. 2009. Use and misuse of the reduced major axis for linefitting. American Journal of Physical Anthropology 140: 476 -486. Richard Smith & 3 friends : קריאה Sokal & Rohlf 1995. Biometry. 3 rd edition. Pages 392 -409 (especially 406 -407 for normality)

Always look at your data Don’t just rely on the statistics! Anscombe's quartet Summary statistics are the same for all four data sets: • • mean (7. 5), standard deviation (4. 12) correlation (0. 816) regression line (y = 3 + 0. 5 x) Anscombe 1973. Graphs in statistical analysis. The American Statistician 27: 17– 21. Briggs Henan University 2010 40

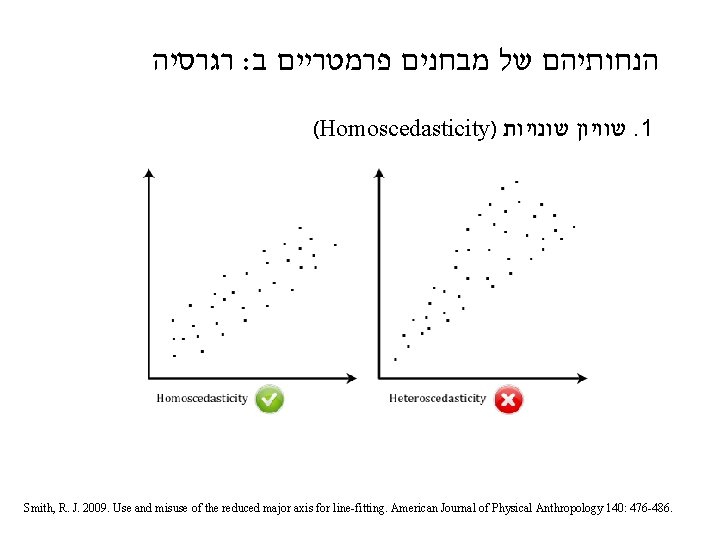
רגרסיה : הנחותיהם של מבחנים פרמטריים ב (Homoscedasticity) שוויון שונויות. 1 Smith, R. J. 2009. Use and misuse of the reduced major axis for line-fitting. American Journal of Physical Anthropology 140: 476 -486.

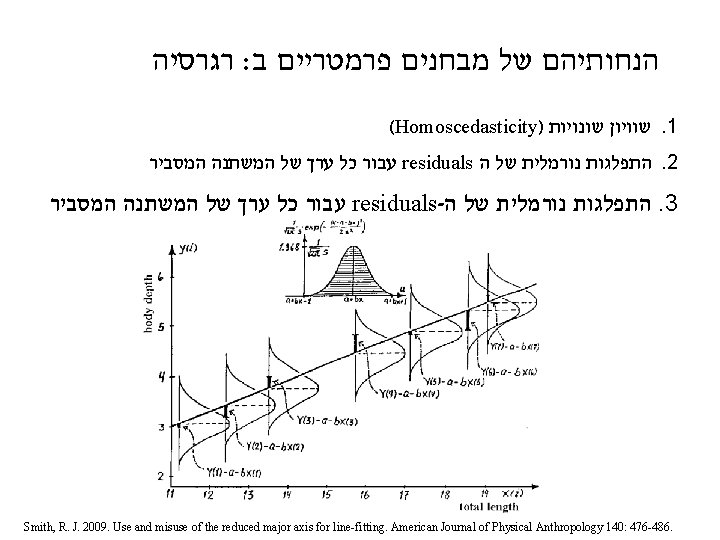
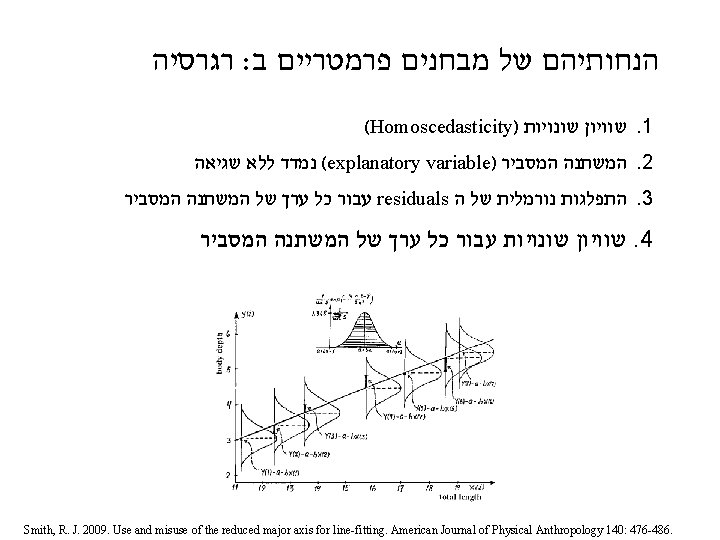
רגרסיה : הנחותיהם של מבחנים פרמטריים ב (Homoscedasticity) שוויון שונויות. 1 ( נמדד ללא שגיאה explanatory variable) המשתנה המסביר. 2 Smith, R. J. 2009. Use and misuse of the reduced major axis for line-fitting. American Journal of Physical Anthropology 140: 476 -486.









R- פרמטריים ב - מבחנים א Orycteropus afer למצולם אין קשר להרצאה פרטרי להשוואת שתי התפלגויות - סמירנוב הוא מבחן א - קולמוגורוב שכיחויות )או השוואת התפלגות "שלנו" להתפלגות ידועה – דוגמת ( הנורמלית נאמר שאנו רוצים להשוות בין : response- ואת ה grouping variable- את ה R- צריך להגדיר ל : התפלגויות השכיחויות של מסת הגוף של לטאות באיי מדף יבשת ואיים אוקייניים island<-read. csv("island_type_final 2. csv", header=T) attach(island) levels(type) [1] "Continental" "Land_bridge" "Oceanic“ Land_bridge<-mass[type=="Land_bridge"] Two-sample Kolmogorov-Smirnov test Oceanic <-mass[type==" Oceanic"] data: Land_bridge and Oceanic ks. test(Land_bridge, Oceanic) D = 0. 1955, p-value = 0. 1288 alternative hypothesis: two-sided

R- פרמטריים ב - מבחנים א t פרטרי המחליף מבחן - הוא מבחן א Mann-Whitney U = Wilcoxon rank sum ? (Lacertidae) ( בין זכרים ונקבות של לטאות SVL) האם יש הבדל בגודל הגוף ssd<-read. table("dimorphism. txt", header=T) attach(ssd) names(ssd) [1] "binomial" "sex" "svl" male<-svl[sex=="male"] female<-svl[sex=="female"] wilcox. test(male, female, paired=FALSE) Wilcoxon rank sum test with continuity correction data: male and female W = 15396, p-value = 0. 1493 alternative hypothesis: true location shift is not equal to 0

R- פרמטריים ב - מבחנים א paired-t מחליף מבחן Wilcoxon two-sample (=Wilcoxon signed-rank) test ( כאשר Lacertidae) ( בין זכרים ונקבות של לטאות SVL) האם יש הבדל בגודל הגוף ? משווים בין הזוויגים של אותו מין ssd<-read. table("dimorphism. txt", header=T) attach(ssd) names(ssd) [1] "binomial" "sex" "svl" male<-svl[sex=="male"] female<-svl[sex=="female"] wilcox. test(male, female, paired=TRUE) Wilcoxon rank sum test with continuity correction data: male and female V = 8822. 5, p-value = 1. 773 e-06 alternative hypothesis: true location shift is not equal to 0

R- פרמטריים ב - מבחנים א paired-t מחליף מבחן Wilcoxon two-sample (=Wilcoxon signed-rank) test ( כאשר Lacertidae) ( בין זכרים ונקבות של לטאות SVL) האם יש הבדל בגודל הגוף ? משווים בין הזוויגים של אותו מין names(ssd) [1] "binomial" "sex" "svl" wilcox. test(male, female, paired=TRUE) אנחנו רוצים שהמבחן יהיה מזווג לפי המין : אבל יש כאן בעיה ! ( – אבל בשום מקום לא הגדרנו זאת binomial) Wilcoxon rank sum test with continuity correction data: male and female V = 8822. 5, p-value = 1. 773 e-06 alternative hypothesis: true location shift is not equal to 0


R- פרמטריים ב - מבחנים א paired-t מחליף מבחן Wilcoxon two-sample (=Wilcoxon signed-rank) test ? האם יש הבדל בגודל הגוף של זכרים ונקבות של לטאות כאשר משווים בין הזוויגים של אותו מין )מה בעצם נהפוך את הנתונים למטריצה : recast- נשתמש ב ( שבדרך כלל מנסים להמנע ממנו בעבודה עם תוכנות סטטיסטיות sex<-recast(ssd, binomial~sex, measure. var = "svl") names(sex) [1] "binomial" "female" "male" sex wilcox. test(sex$female, sex$male, paired=TRUE) Wilcoxon signed rank test with continuity correction data: sex$female and sex$male V = 3423. 5, p-value = 1. 773 e-06


R- פרמטריים ב - מבחנים א one-way ANOVA מחליף מבחן Kruskal-Wallis אותו ANOVA הקוד למבחן זה דומה מאוד לקוד של מבחן kruskal. test נכתוב aov רק שבמקום , הוא מחליף island<-read. csv("island_type_final 2. csv", header=T) Attach(island) kruskal. test(clutch~type) Kruskal-Wallis rank sum test data: clutch by type Kruskal-Wallis chi-squared = 7. 1639, df = 2, p-value = 0. 02782

R- פרמטריים ב - מבחנים א מחליפים מבחן קורלציה Kendall’s-tau ומבחן Spearman מבחן על ידי , למעשה הקוד פה הוא וריאציה על הקוד הרגיל למבחן קורלציה “method” פרמטרי הרלוונטי בפרמטר - הוספת ההגדרה למבחן הא נכתוב cor. test(clutch, mass) : במקום לכתוב cor. test(clutch, mass, method="spearman") #or cor. test(clutch, mass, method="kendall") : ונקבל בהתאמה Spearman's rank correlation rho data: clutch and mass S = 1907900, p-value < 2. 2 e-16; rho 0. 5402 Kendall's rank correlation tau data: clutch and mass z = 9. 747, p-value < 2. 2 e 16; tau 0. 4059




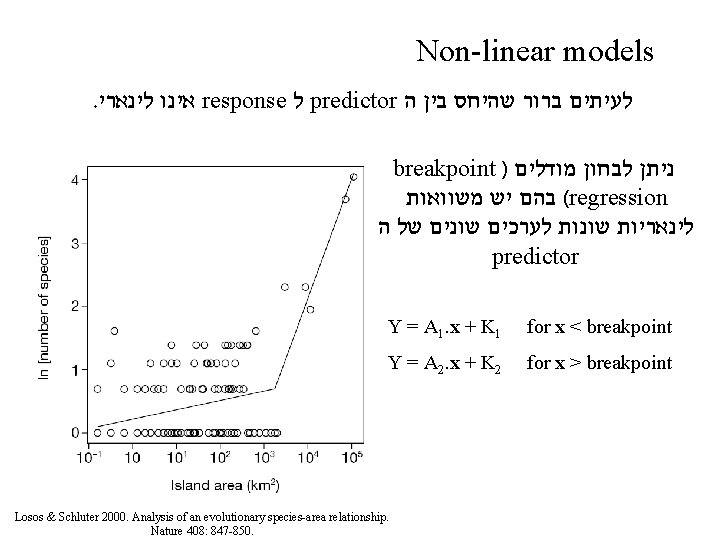
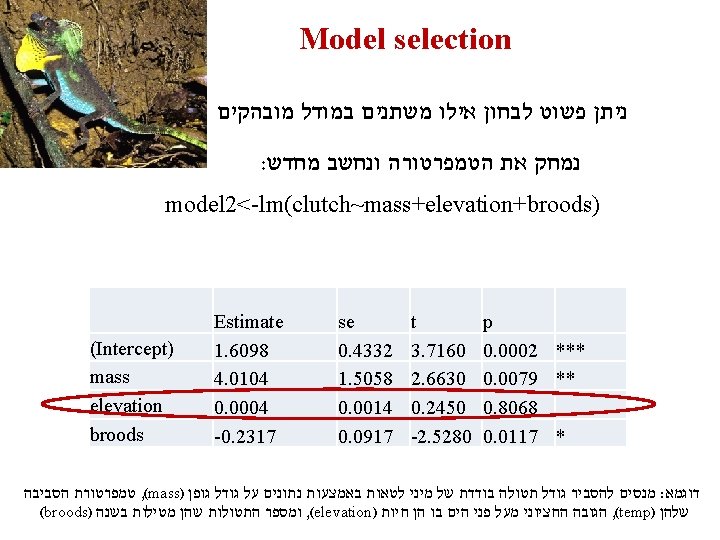
Non-linear models. אינו לינארי response ל predictor לעיתים ברור שהיחס בין ה breakpoint ) ניתן לבחון מודלים ( בהם יש משוואות regression לינאריות שונות לערכים שונים של ה predictor Y = A 1. x + K 1 for x < breakpoint Y = A 2. x + K 2 for x > breakpoint Losos & Schluter 2000. Analysis of an evolutionary species-area relationship. Nature 408: 847 -850.











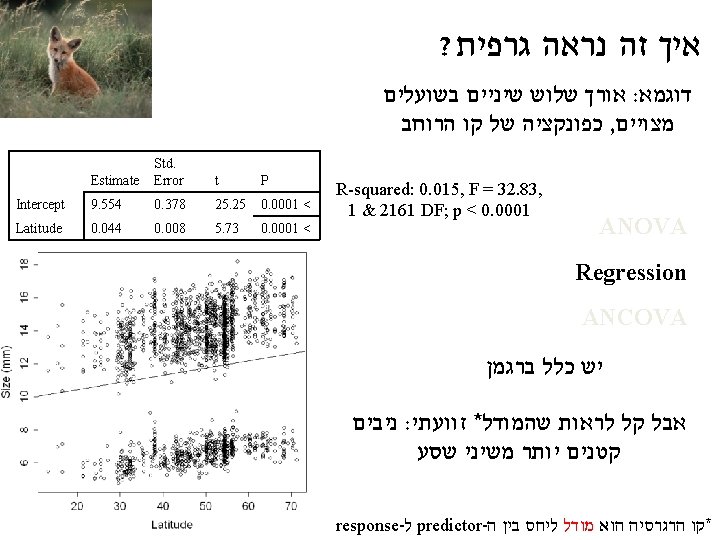
R- ב ANCOVA קריאת תוצאות מודל דוגמא ללא אינטראקציות Response = intercept + a for level 1 of the 1 st categorical predictor variable or + b for level 2 of the 1 st + c for level 1 of the 2 nd categorical predictor or d for level 2… +k*(value of the continuous predictor variable) + error Tooth / sex אם נחזור לשועלים , למשל Latitude factor Estimate Std. Error Intercept (tooth c) 4. 342 0. 078 55. 92 tooth_m 8. 485 0. 038 224. 21 0. 0001< tooth_p 6. 617 0. 038 174. 84 0. 0001< sex_male 0. 391 0. 031 12. 56 0. 0001< Latitude 0. 043 0. 001 29. 06 0. 0001< t p 0. 0001< : ( על פי המודל הוא 32 בזכרים בתל אביב )קו רוחב P כך שהאורך של שן 12. 726 = 4. 342+6. 617+0. 391+32*0. 043





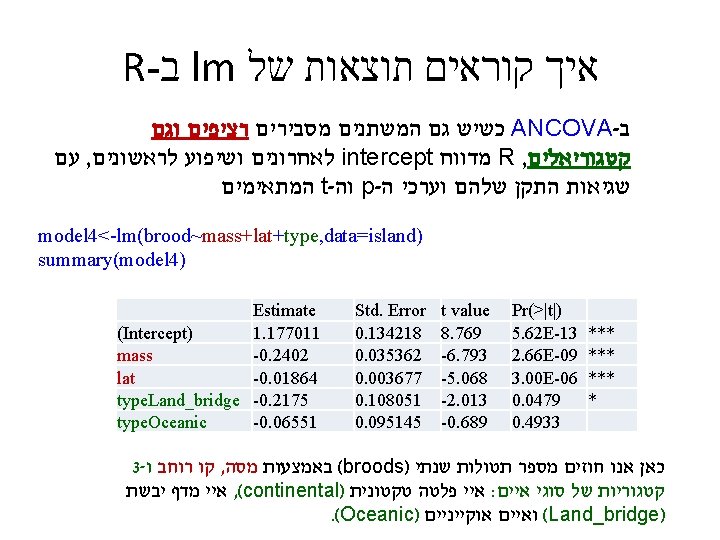
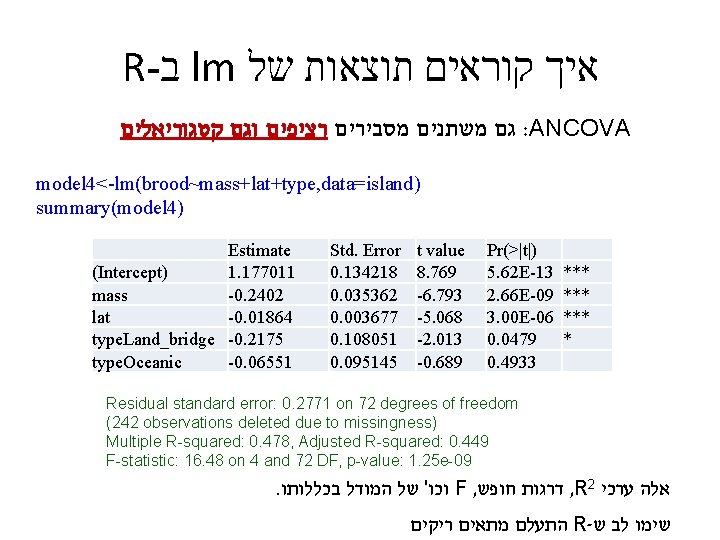
R- ב lm איך קוראים תוצאות של גם משתנים מסבירים רציפים וגם קטגוריאלים : ANCOVA model 4<-lm(brood~mass+lat+type, data=island) summary(model 4) Estimate (Intercept) 1. 177011 mass -0. 2402 lat -0. 01864 type. Land_bridge -0. 2175 type. Oceanic -0. 06551 Std. Error 0. 134218 0. 035362 0. 003677 0. 108051 0. 095145 t value 8. 769 -6. 793 -5. 068 -2. 013 -0. 689 Pr(>|t|) 5. 62 E-13 2. 66 E-09 3. 00 E-06 0. 0479 0. 4933 *** *** * Residual standard error: 0. 2771 on 72 degrees of freedom (242 observations deleted due to missingness) Multiple R-squared: 0. 478, Adjusted R-squared: 0. 449 F-statistic: 16. 48 on 4 and 72 DF, p-value: 1. 25 e-09 . וכו' של המודל בכללותו F , דרגות חופש , R 2 אלה ערכי התעלם מתאים ריקים R- שימו לב ש



relevel (2) model 4<-lm(brood~mass+lat+type, data=island) summary(model 4) אליו הוא ישווה את , מי יהיה הגורם הראשון R- להגדיר ל : אפשר להתחכם : relevel על ידי הפקודה , האחרים model 4 a<-lm(brood~mass+lat+relevel(type, "Land_bridge"), data=island) summary(model 4 a) או model 4 b<-lm(brood~mass+lat+relevel(type, "Oceanic"), data=island) summary(model 4 b)

relevel (3) אליו הוא ישווה את , מי יהיה הגורם הראשון R- להגדיר ל : אפשר להתחכם : relevel על ידי הפקודה , האחרים model 4 a<-lm(brood~mass+lat+relevel(type, "Land_bridge"), data=island) summary(model 4 a) Estimate (Intercept) mass lat relevel(type, Land_bridge)Continental relevel(type, Land_bridge)Oceanic Std. Error 0. 95951 -0. 2402 -0. 01864 0. 217501 0. 151989 T value 0. 148951 0. 035362 0. 003677 0. 108051 0. 080072 t 6. 442 -6. 793 -5. 068 2. 013 1. 898 Pr(>|t|) 1. 16 E-08 2. 66 E-09 3. 00 E-06 0. 0479 0. 0617 *** *** *. : שימו לב שהפרמטרים של המודל הכללי נשארו זהים Residual standard error: 0. 2771 on 72 degrees of freedom (242 observations deleted due to missingness) Multiple R-squared: 0. 478, Adjusted R-squared: 0. 449 F-statistic: 16. 48 on 4 and 72 DF, p-value: 1. 25 e-09

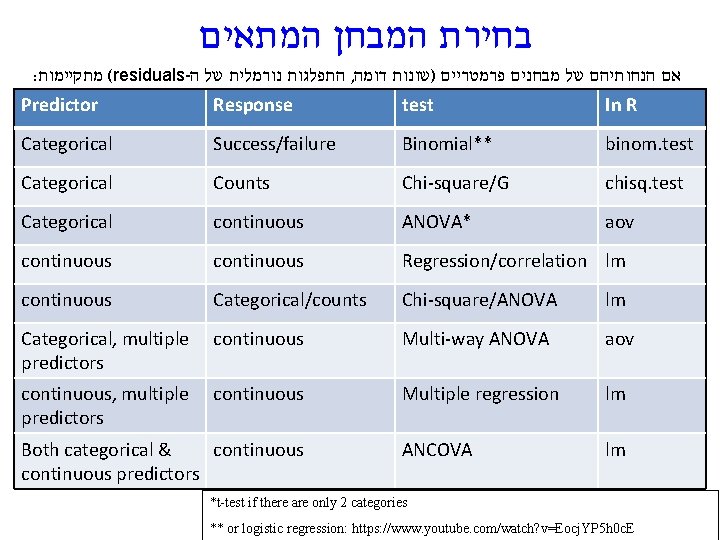
בחירת המבחן המתאים : ( מתקיימות residuals- התפלגות נורמלית של ה , אם הנחותיהם של מבחנים פרמטריים )שונות דומה Predictor Response test In R Categorical Success/failure Binomial** binom. test Categorical Counts Chi-square/G chisq. test Categorical continuous ANOVA* aov continuous Regression/correlation lm continuous Categorical/counts Chi-square/ANOVA lm Categorical, multiple predictors continuous Multi-way ANOVA aov continuous, multiple predictors continuous Multiple regression lm ANCOVA lm Both categorical & continuous predictors *t-test if there are only 2 categories ** or logistic regression: https: //www. youtube. com/watch? v=Eocj. YP 5 h 0 c. E














Model selection Akaike Information Criterion Hirotsugu Akaike AIC = 2 k-2 ln(L) שימו לב שהתמיכה במודל חזקה יותר ככל : נמוך יותר AIC שערך ה AIC rewards descriptive accuracy via the maximum likelihood (High L), and penalizes lack of parsimony according to the number of free parameters (high K) : פשוטה מאוד AIC השוואת מודלים לפי R- ב AIC(model 1, model 2, model 3)




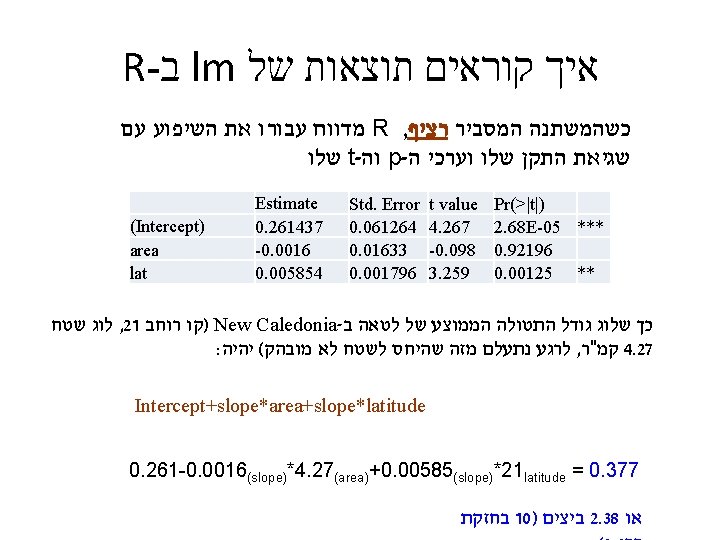
![Model selection variation on the AIC theme AICc AIC2 kk1nk1 AICc 1 עבור Model selection: variation on the AIC theme AICc = AIC+(2 k*[k+1]/[n-k-1]) AICc. 1 עבור](https://slidetodoc.com/presentation_image_h2/635c97bcd88288a5ca911a4004be8e6e/image-103.jpg)
Model selection: variation on the AIC theme AICc = AIC+(2 k*[k+1]/[n-k-1]) AICc. 1 עבור מדגמים קטנים AIC תיקון ל (http: //cran. r-project. org/web/packages/AICcmodavg. pdf R )חבילת AIC weights. 2 “Akaike weights are used in model averaging. They represent the relative likelihood of a model. To calculate them, for each model first calculate the relative likelihood of the model, which is just exp(-0. 5 * ∆AIC score for that model). The Akaike weight for a model is this value divided by the sum of these values across all models. ” † Baysian Information Criterion, BIC. 3 למספרים גדולים AIC מ 1 סובלני פחות †† של פרמטרים BIC: -2*ln L + k*ln(n) † http: //www. brianomeara. info/tutorials/aic Aho et al. 2014. Model selection for ecologists: the worldviews of AIC and BIC. Ecology, 95: 631 -636. †† Wagenmakers & Farrell 2004 גודל המדגם לא משחק AIC- ב , ! מוכפל בגודל המדגם k : שימו לב. 1

: בכל עבודה , זיכרו "No statistical procedure can substitute for serious thinking about alternative evolutionary scenarios and their credibility" Westoby, Leishman & Lord 1995. On misinterpreting 'phylogenetic correction. J. of Ecology 83: 531 -534.