1 Analysis Toolkit Using Graphs in Economic Analysis

1 Analysis Toolkit ■Using Graphs in Economic Analysis

Using Graphs in Economic Analysis ● Display large quantity of data quickly ● Facilitate data interpretation and analysis ● Important relationships more apparent than from written descriptions or long lists of numbers

Two-Variable Diagrams ● Variable = an entity that can assume different values. ● Variable can be independent (usually represented on the X-axis) or dependent (usually represented on the Y-axis) ● In microeconomics, we will study such variables as prices, quantity, revenue, cost and profit.

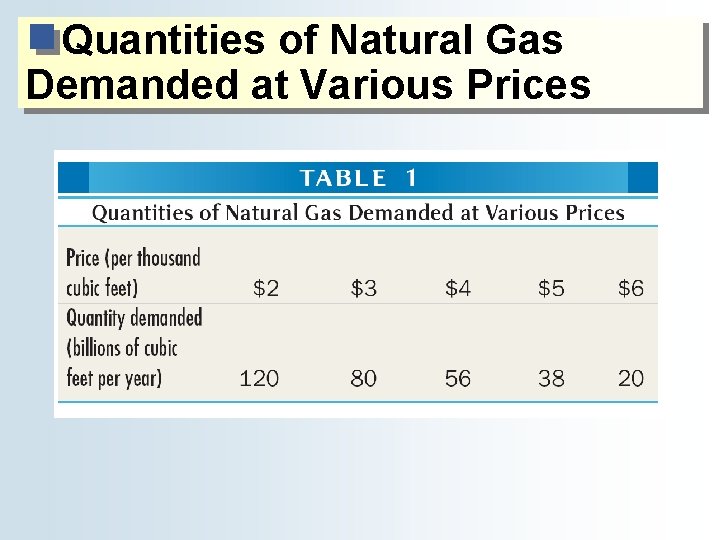
Quantities of Natural Gas Demanded at Various Prices

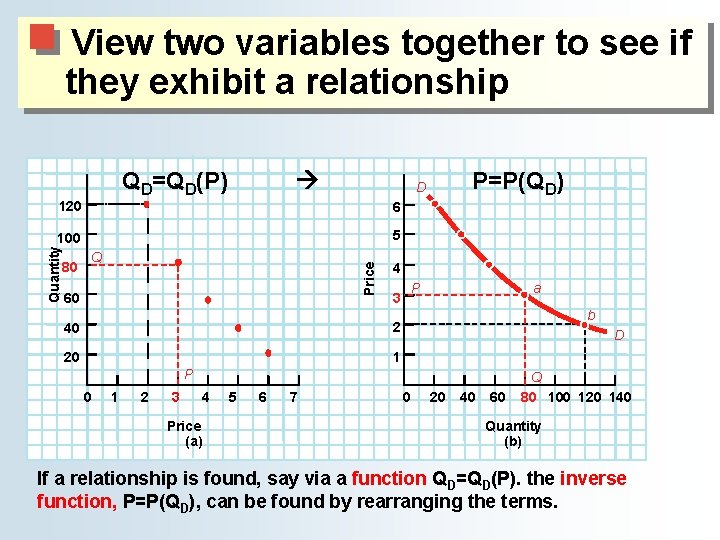
View two variables together to see if they exhibit a relationship QD=QD(P) 6 100 5 Q Price Quantity 120 80 60 P=P(QD) D 4 P 3 40 2 20 1 a b D P 0 1 2 3 4 Price (a) 5 6 7 0 20 40 60 Q 80 100 120 140 Quantity (b) If a relationship is found, say via a function QD=QD(P). the inverse function, P=P(QD), can be found by rearranging the terms.

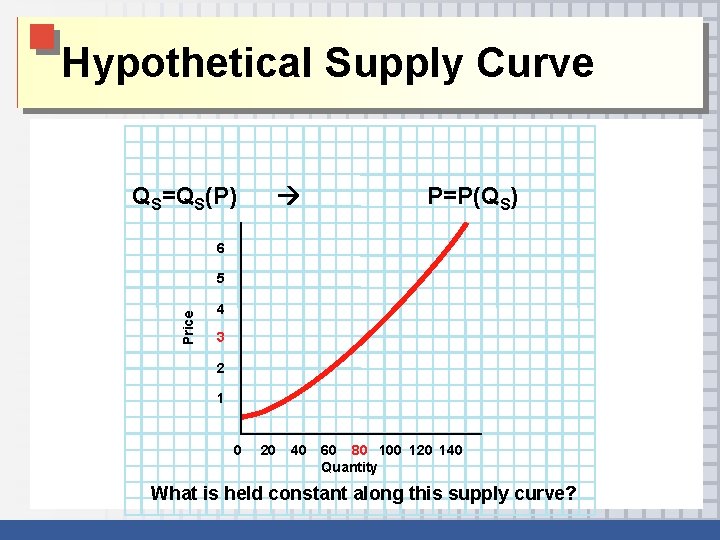
Hypothetical Supply Curve QS=QS(P) P=P(QS) 6 Price 5 4 3 2 1 0 20 40 60 80 100 120 140 Quantity What is held constant along this supply curve?

The Definition and Measurement of Slope ● Slope = ratio of vertical change to horizontal change Y ♦ Rise divided by Run= X ♦ Measure of steepness of a relationship

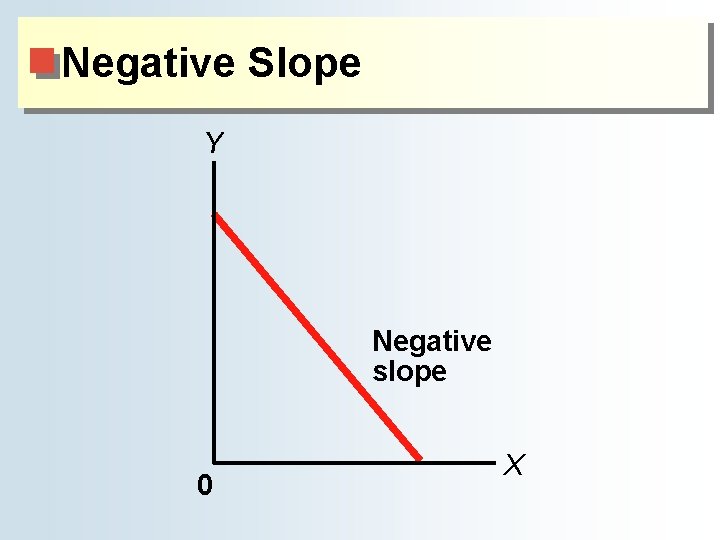
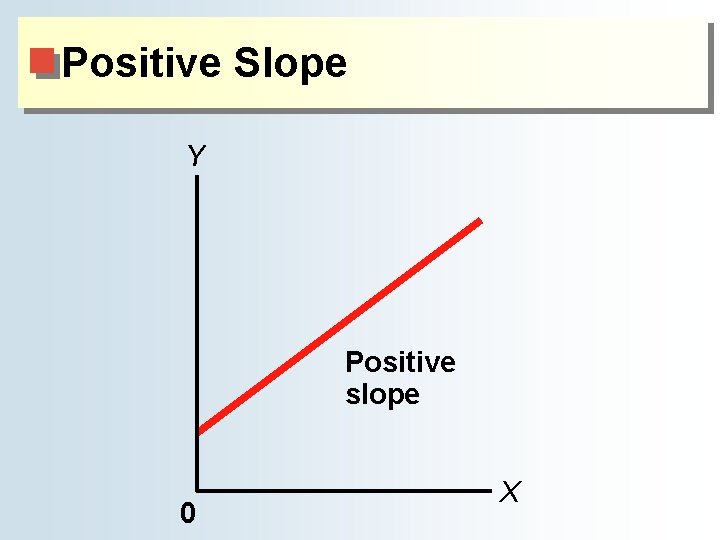
The Definition and Measurement of Slope ● The slope of a straight line ♦ Negative slope = one variable rises while the other variable falls ■ The two variables move in opposite directions. ♦ Positive slope = two variables rise and fall together ■ The two variables move in the same direction.

Negative Slope Y Negative slope 0 X

Positive Slope Y Positive slope 0 X

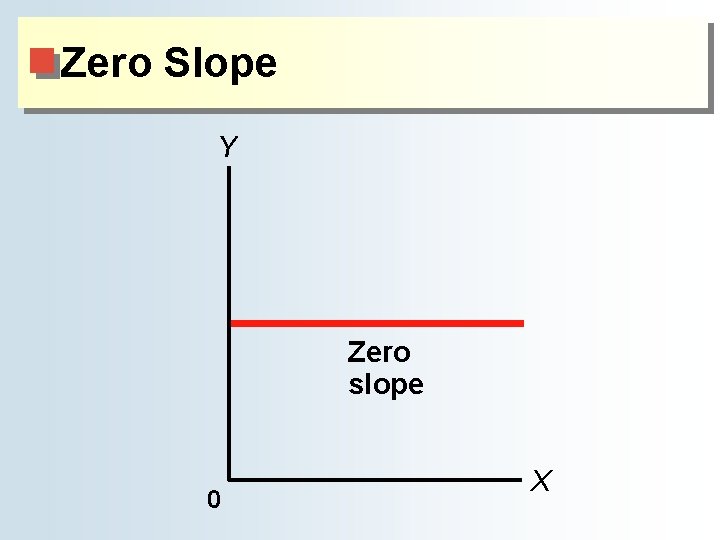
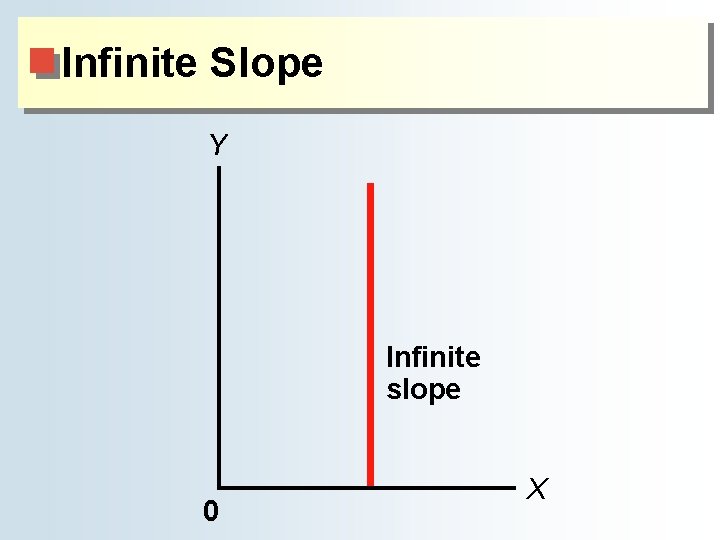
The Definition and Measurement of Slope ♦ Zero slope = the variable on the horizontal axis can be any value while the variable on the vertical axis is fixed ■ Horizontal line ♦ Infinite slope = the variable on the vertical axis can be any value while the variable on the horizontal axis is fixed ■ Vertical line

Zero Slope Y Zero slope 0 X

Infinite Slope Y Infinite slope 0 X

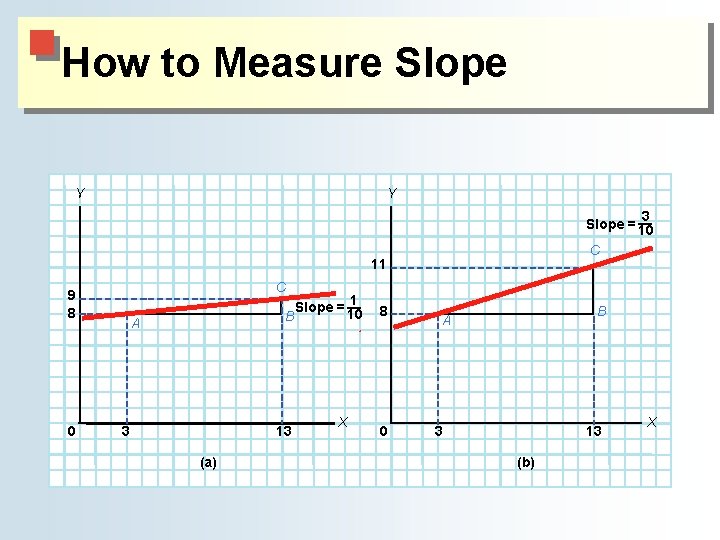
The Measurement of Slope ● The slope of a straight line ♦ Slope is constant along a straight line. ♦ Slope can be measured between any two points on one axis and the corresponding two points on the other axis.

How to Measure Slope Y Y 3 Slope = — 10 C 11 C 9 8 0 1 Slope = — 10 B A 3 13 (a) X 8 0 B A 3 13 (b) X

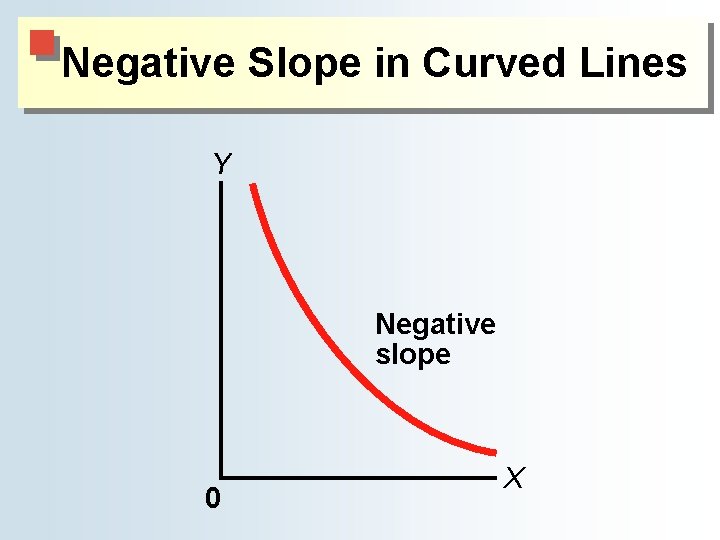
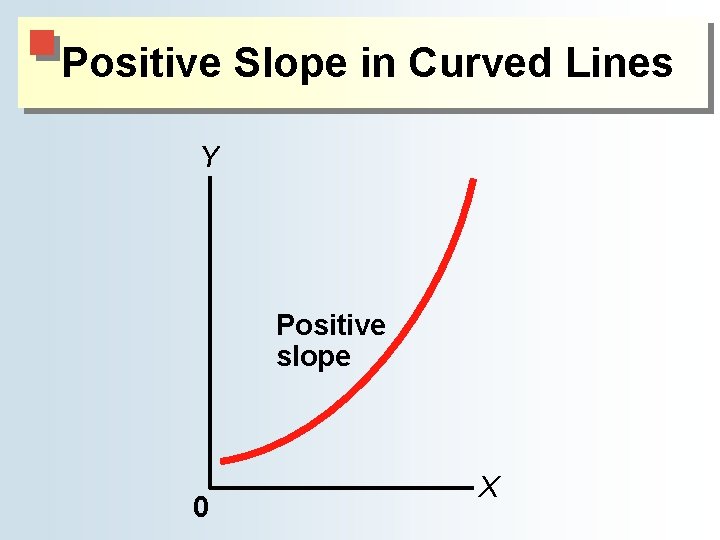
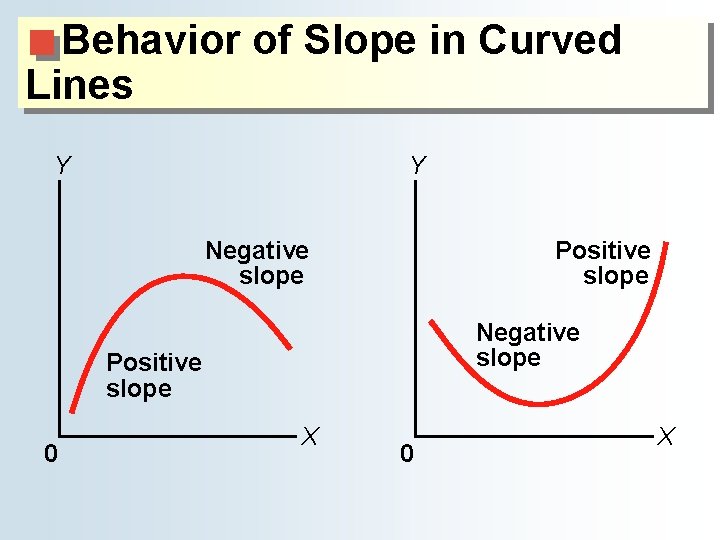
The Definition and Measurement of Slope ● The slope of a curved line ♦ Slope changes from point to point on a curved line. ■Curved line bowed toward the origin has a negative slope. ● Variables change in opposite directions. ■Curved line bowed away from the origin has a positive slope. ● Variables change in the same direction.

Negative Slope in Curved Lines Y Negative slope 0 X

Positive Slope in Curved Lines Y Positive slope 0 X

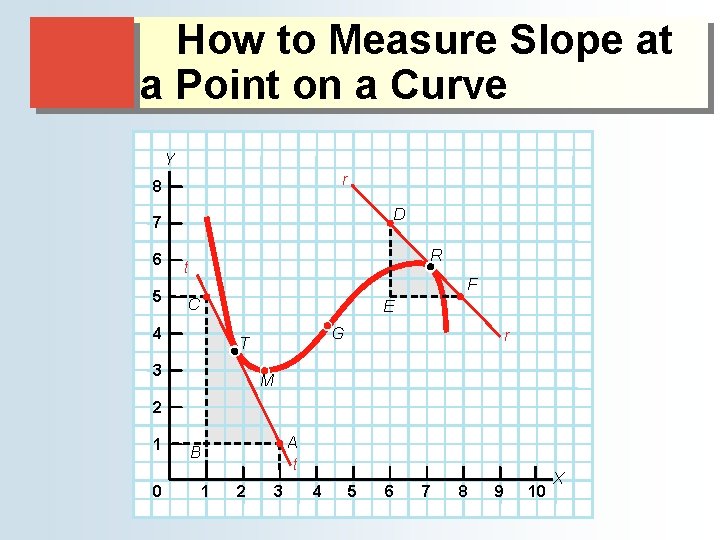
The Definition and Measurement of Slope ● The slope of a curved line ♦ A curved can have both a positive and negative slope depending on where on the curve is measured. ♦ The slope at a point on a curved-line is measured by a line tangent to that point.

Behavior of Slope in Curved Lines Y Y Negative slope Positive slope 0 X

How to Measure Slope at a Point on a Curve Y r 8 D 7 6 5 R t F C E 4 G T 3 r M 2 1 0 A t B 1 2 3 4 5 6 7 8 9 10 X

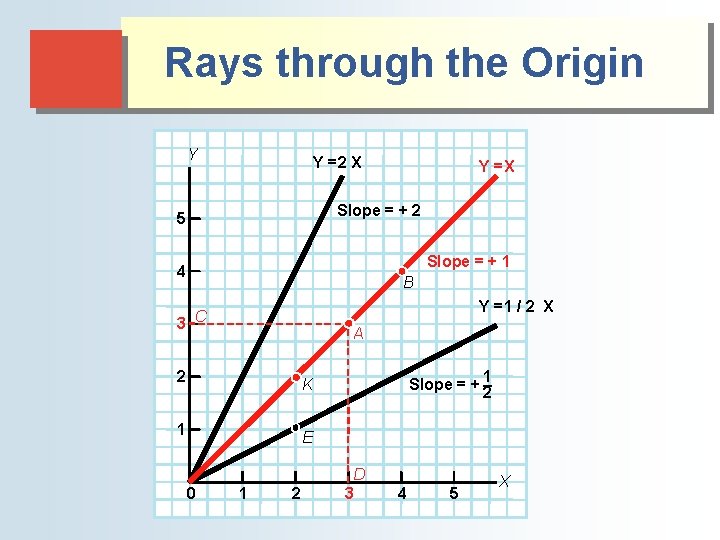
Rays Through the Origin and 45 -degree Lines ● Y-intercept = point at which a line touches the y axis, i. e. when x =0 ● X-intercept = point at which a line touches the x axis, i. e. when y =0 ● Ray through the origin = straight line graph with a y-intercept of zero

Rays through the Origin Y Y =2 X Y =X Slope = + 2 5 Slope = + 1 4 B Y =1 / 2 X 3 C A 2 K 1 E 0 1 2 Slope = + 1 – 2 D 3 4 5 X

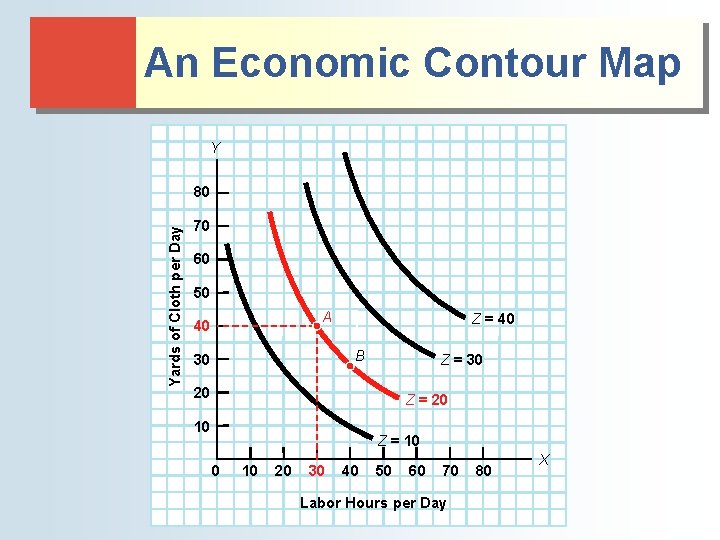
Squeezing 3 Dimensions into 2: Contour Maps ● Some problems involve more than two variables ● Economic “contour map” a. k. a. indifference map or level set. ♦ Shows how variable Z changes as we change either X or Y

An Economic Contour Map

An Economic Contour Map Y Yards of Cloth per Day 80 70 60 50 A 40 Z = 40 B 30 Z = 30 20 Z = 20 10 Z = 10 0 10 20 30 40 50 60 70 Labor Hours per Day 80 X