1 A ship has a displacement of 2

• 1. A ship has a displacement of 2, 400 tons and KG 10. 8 meters. Find the new KG if a weight of 50 tons mass already on board is raised 12 meters vertically. • Answer: 11. 05 meters

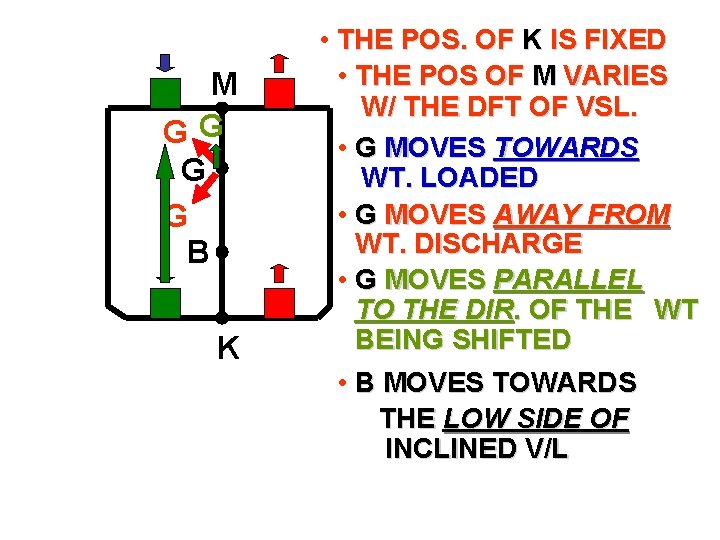
M GG G G B K • THE POS. OF K IS FIXED • THE POS OF M VARIES W/ THE DFT OF VSL. • G MOVES TOWARDS WT. LOADED • G MOVES AWAY FROM WT. DISCHARGE • G MOVES PARALLEL TO THE DIR. OF THE WT BEING SHIFTED • B MOVES TOWARDS THE LOW SIDE OF INCLINED V/L

M G K

• 1. Solution: • GG’ = Wt. x Dist. Δ • = 50 tons x 12 m 2, 400 tons • GG’ = 0. 25 m • Old KG = 10. 80 m ( + ) • New KG = 11. 05 m

• 2. A ship has displacement of 2, 000 tons and KG 10. 5 meters. Find the new KG if a weight of 40 tons mass already on board is shifted from the ‘tween deck to lower hold trough a distance of 4. 5 meters vertically. • Ans. 10. 41 m

M G K

• 2. Solution: • GG’ = Wt x Dist Δ • = 40 tons x 4. 5 m 2, 000 tons • GG’ = 0. 09 m • Old KG = 10. 50 m ( - ) • New KG = 10. 41 m

3. A ship of 2, 000 tons displacement has KG 4. 5 meters. A heavy lift of 20 tons mass is in the lower hold and has KG 2 meters. The weight is then raised 0. 5 meter clear of the tank top by a derrick whose head is 14 meters above the keel. Find the new KG of the ship? Ans. 4. 62 m

M G K

• • • 3. Solution: Height of Derrick fr. Keel = 14 m KG. of Cargo = 2. 0 m ( - ) Distance = 12. 0 m GG’ = Wt x Dist. Δ = 20 tons x 12. 0 m 2, 000 tons GG’ = 0. 12 m Old KG = 4. 50 m ( + ) New KG = 4. 62 m

4. A ship has a displacement of 7, 000 tons and KG 6 meters. A heavy lift in the lower hold has KG 3 meters and mass 40 tons. Find the new KG when this weight is raised through 4. 5 meters vertically and is suspended by a derrick whose head is 17 meters above the keel. Ans. 6. 08 m

• 4. Solution: • Ht of Derrick = 17. 0 m • KG of Cargo = 3. 0 m ( - ) • Distance = 14. 0 m • GG’ = Wt. x Dist. Δ • = 40 tons x 14. 0 m 7, 000 tons • GG’ = 0. 08 m • Old KG = 6. 00 m ( + ) • New KG = 6. 08 m

5. Find the ship in the center of gravity of a ship of 1, 500 tons displacement when a weight of 25 tons mass is shifted from the starboard side of the lower hold to the port side on deck through a distance of 15 meters. Ans. 0. 25 m

• 5. Solution: • GG’ = Wt. x Dist. Δ • = 25 tons x 15 m 1, 500 tons • GG’ = 0. 25 m

6. A tank holds 120 tons when full of fresh water. Find how many tons of oil of relative density 0. 84 it will hold, allowing 2% of the volume of the tank for expansion in the oil. Ans. 98. 78 tons

• 6. Solution: • Capacity = Wt. of FW x Expansion • = 120 tons x 2 % or (. 02 ) • Capacity = 2. 4 • (-) 120. 0 • Capacity = 117. 6 tons • Wt. of Oil = Capacity x R. D. of Oil • 117. 6 tons x 0. 84 • Wt. of oil = 98. 78 tons

7. A tank when full will hold 130 tons of salt water. Find how many tons of oil relative density 0. 909 it will hold allowing 1% of the volume of the tank for expansion. Ans. 114. 13 tons

• • • 7. Solution: Capacity = Capacity of FW x Expansion = 130 x 1% or. 01 Capacity = 1. 3 (-) 130. 0 tons Capacity = 128. 7 tons R. D. Oil = 0. 909 ( x ) Wt. of Oil = 116. 98 tons Actual Wt. = Weight of Oil / Density of SW = 116. 98 tons / 1. 025 Actual Wt. of Oil = 114. 13 tons

8. A tank measuring 8 m x 6 m x 7 m is being filled with oil of relative density 0. 9. Find how many tons of oil in the tank when the ullage is 3 meters. Ans. 172. 8 tons

• 8. Solution: • Wt. of Oil = L x W x (H – Ullage) x R. D of Oil • = 8 m x 6 m x ( 7 m – 3 m ) x 0. 9 • = 8 m x 6 m x 4 m x 0. 9 • Wt. of Oil = 172. 8 tons

9. Oil of relative density 0. 75 is run into a tank measuring 6 m x 4 m x 8 m until the ullage is 2 meters. Calculate the number of tons of oil the tank then contains Ans. 108 tons

• 9. Solution: Weight of Oil = L x W x ( H – Ullage ) x R. D. Oil = 6 m x 4 m x (8 m – 2 m) x 0. 75 = 6 m x 4 m x 6 m x 0. 75 Weight of Oil = 108 tons

10. A tank will hold 100 tons when full of fresh water. Find how many tons of oil of relative density 0. 85 may be loaded if 2% of the volume of the oil loaded is to be allowed for expansion. Ans. 83. 3 tons

• • • 10. Solution: Capacity = Wt. of FW x Expansion = 100 t x 2% or. 02 = 2 (-)100 Capacity = 98 tons Weight of Oil = Capacity x R. D. of Oil = 98 tons x 0. 85 Weight of Oil = 83. 3 tons

11. A box-shaped vessel 120 m x 6 m x 2. 5 m floats at a draft of 1. 5 m in water of density 1, 013 kgs/m³. Find the displacement in tons, and the height of the centre of buoyancy above the keel. Ans. 1094. 04 tons / 0. 75 m

• 11. Solution: • Δ = L x B x Draft x Cb x R. Density • = 20 m x 6 m x 1. 5 m x 1. 013 tons/m³ • Δ = 1, 094. 04 tons • KB = ½ x Draft • = ½ x 1. 5 m • KB = 0. 75 m

• 12. A box-shaped barge 55 m x 10 m x 6 m is floating in fresh water on an even keel at 1. 5 m draft. If 1, 800 tons of cargo is now loaded, find the difference in the height of the centre buoyancy above the keel? • Ans. 1. 636 m

• • • 12. Solution: Δ = L x W x Draft x Cb x R. Density = 55 m x 10 m x 1. 5 m x 1. 000 ton/m³ Δ = 825 tons KB = ½ x Draft KB = ½ x 1. 5 m KB = 0. 75 m

• If 1, 800 is now loaded • Δ = L x W x Draft x Cb x R. Density • 1, 800 tons = 55 m x 10 m x Draft x 1. 000 • Draft = 1800 tons • 55 m x 10 m x 1. 000 ton/m³ • Draft = 1800 • 550 • Draft = 3. 27 m • KB = ½ x Draft • = ½ x 3. 27 m • KB = 1. 635 m

• 12. Solution: • New Draft • Old Draft • New Draft 1. 5 m • New Draft = • • New Δ Old Δ 1, 800 tons 825 tons 1. 5 m x 1, 800 tons 825 tons New Draft = 3. 27 m KB = ½ x Draft KB = ½ x 3. 27 m KB = 1. 635 m

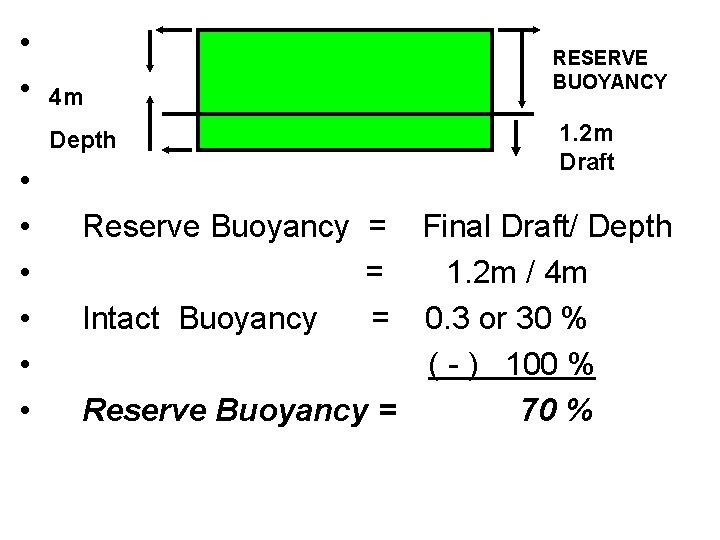
13. A box-shaped barge 75 m x 6 m x 4 m displaces 180 tons when light. If 360 tons of iron are loaded while the barge is floating in fresh water, find her final draft reserve buoyancy. Ans. 1. 2 m / 70%

• 13. Solution: Light Δ = L x W x Draft x Cb x R. Density 180 tons = 75 m x 6 m x Draft x 1. 0 Light Draft = 180 tons 75 m x 6 m x 1. 000 Light Draft = 180 tons 450 Light Draft = 0. 4 m

• New Draft Old Draft New Draft 0. 4 m New Draft = New Δ Old Δ • 360 tons 180 tons • 0. 4 m x 360 tons 180 tons • New Draft = 0. 8 m • Light Draft = 0. 4 m ( + ) • Final Draft = 1. 2 m

• • 4 m Depth • • • Reserve Buoyancy = = Intact Buoyancy = RESERVE BUOYANCY 1. 2 m Draft Final Draft/ Depth 1. 2 m / 4 m 0. 3 or 30 % ( - ) 100 % Reserve Buoyancy = 70 %