1 A Case for Using Signal Transition Graphs

1 A Case for Using Signal Transition Graphs for Analysing and Refining Genetic Networks Richard Banks, Victor Khomenko and Jason Steggles School of Computing Science, Newcastle University, UK

Overview • Modelling genetic regulatory networks using Boolean networks (BNs). • Problems with BN approach. • Asynchronous circuit design techniques. • A refinement approach based on Signal Transition Graphs (STGs). • Case study on lysis-lysogeny switch in Lambda phage. • Conclusions and future work. 2

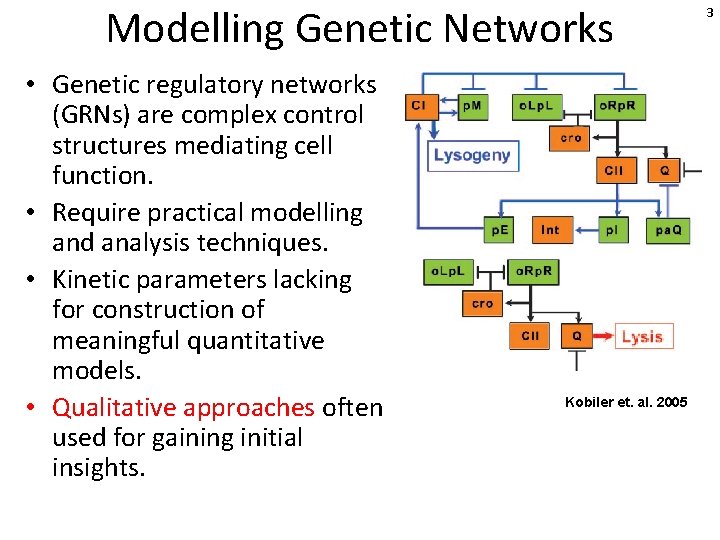
Modelling Genetic Networks • Genetic regulatory networks (GRNs) are complex control structures mediating cell function. • Require practical modelling and analysis techniques. • Kinetic parameters lacking for construction of meaningful quantitative models. • Qualitative approaches often used for gaining initial insights. Kobiler et. al. 2005 3

Boolean Networks • Qualitative model: Boolean networks (BNs). • Regulatory entities abstracted to binary switches. • Behaviour of each switch given by Boolean function over inputs. a b c [a] [b] [c] 0 0 1 1 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 0 Circuit equations [a] = b [b] = ac [c] = a • Synchronous or asynchronous interpretation. • BNs circuits. 4

Aim • Synchronous BN interpretation arguably unrealistic. • Asynchronous BNs more realistic, but capture too rich, non-deterministic behaviour unrealisable in practice. • Require realistic qualitative modelling approach with appropriate analysis techniques and tools. Solution: • Use asynchronous approach. • Remove unrealisable behaviour using techniques from asynchronous circuit design. • Based on speed-independent (SI) circuits functions correctly regardless of gate delays. 5

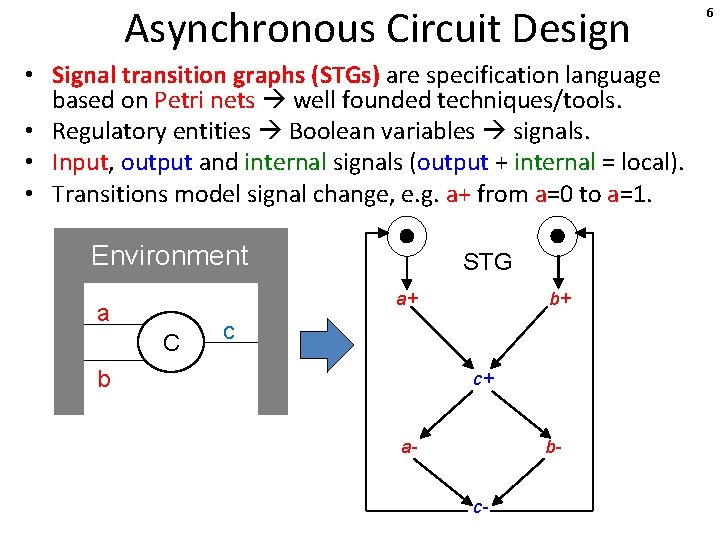
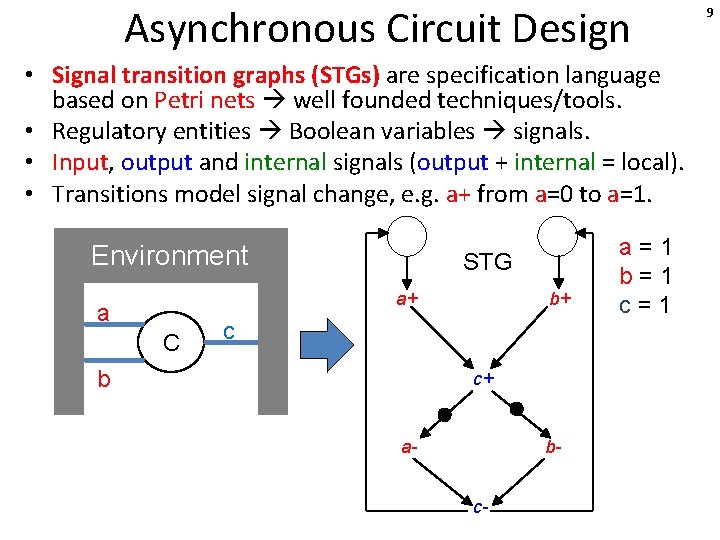
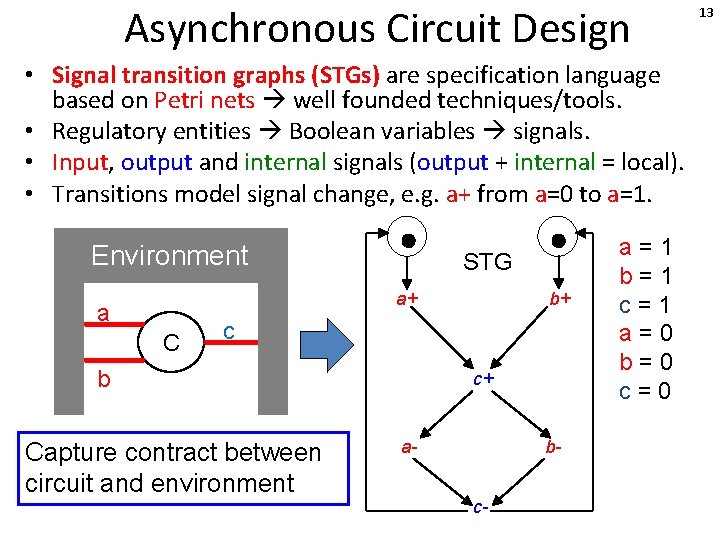
Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b c+ a- bc- 6

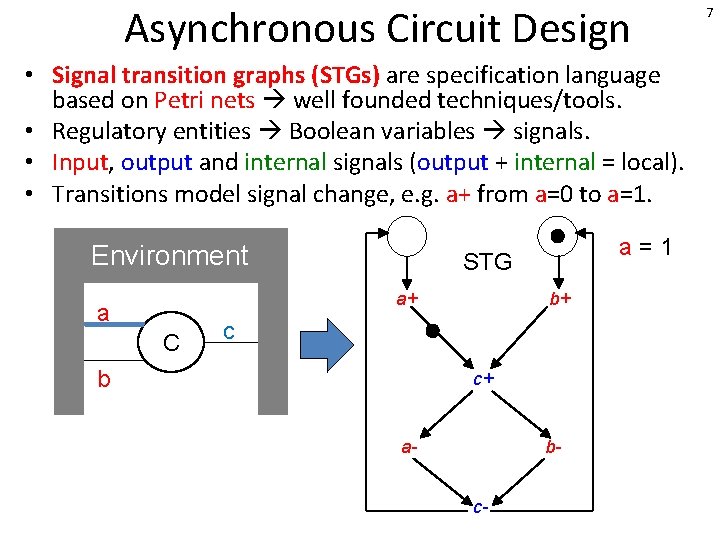
Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C a=1 b+ c b c+ a- bc- 7

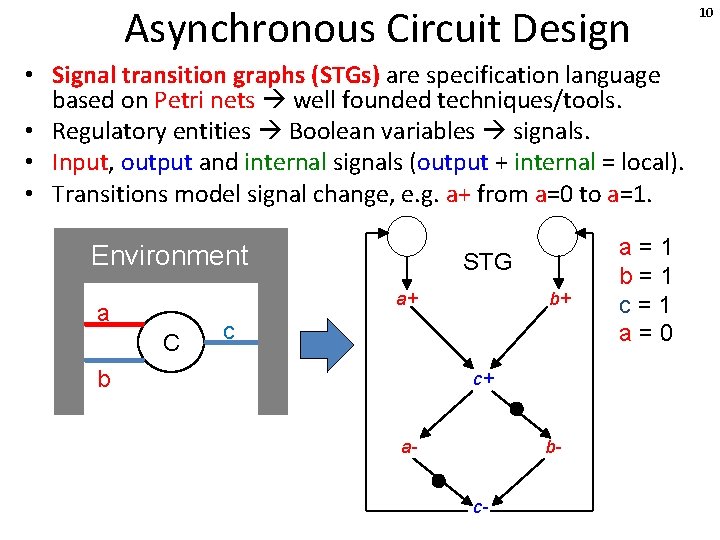
Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C a=1 b+ c b c+ a- bc- 8

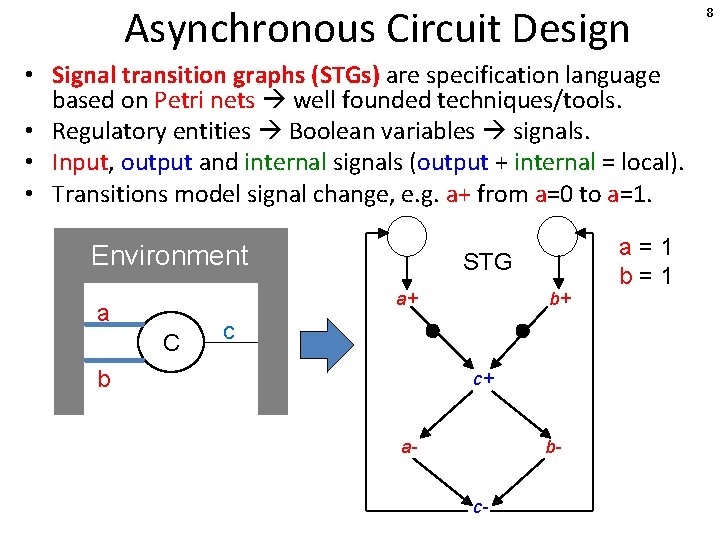
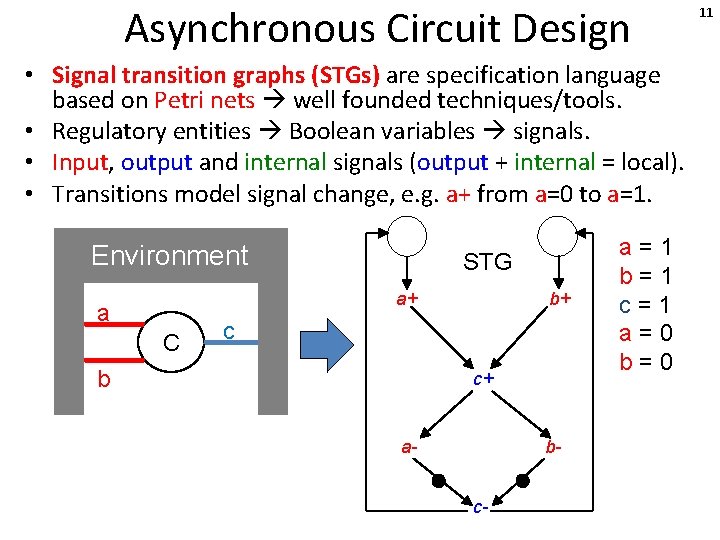
Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b c+ a- bc- a=1 b=1 c=1 9

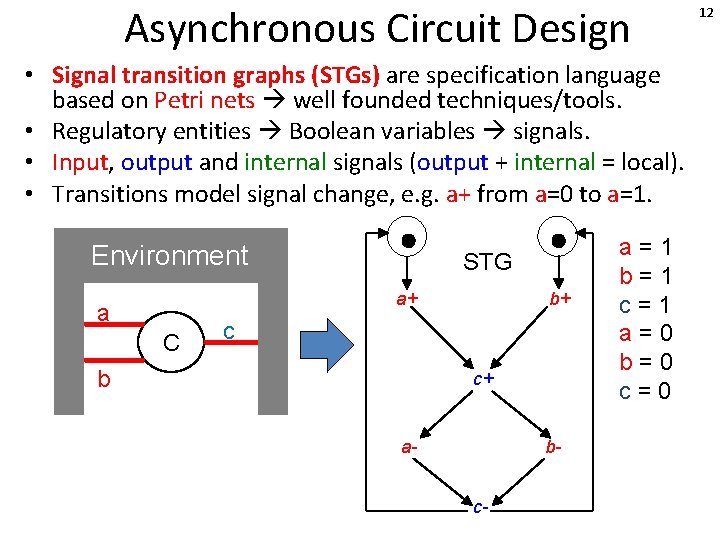
Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b c+ a- bc- a=1 b=1 c=1 a=0 10

Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b c+ a- bc- a=1 b=1 c=1 a=0 b=0 11

Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b c+ a- bc- a=1 b=1 c=1 a=0 b=0 c=0 12

Asynchronous Circuit Design • Signal transition graphs (STGs) are specification language based on Petri nets well founded techniques/tools. • Regulatory entities Boolean variables signals. • Input, output and internal signals (output + internal = local). • Transitions model signal change, e. g. a+ from a=0 to a=1. Environment STG a+ a C b+ c b Capture contract between circuit and environment c+ a- bc- a=1 b=1 c=1 a=0 b=0 c=0 13

Relationship between BNs and STGs a+ b+ Circuit equation (BN) [c] = ab + c(a + b) c+ a- Models most general environment! bc- 14 a- • BN STG straightforward. • Equation loses environmental information STGs more useful b+ for analysis a+ c+ b- c-

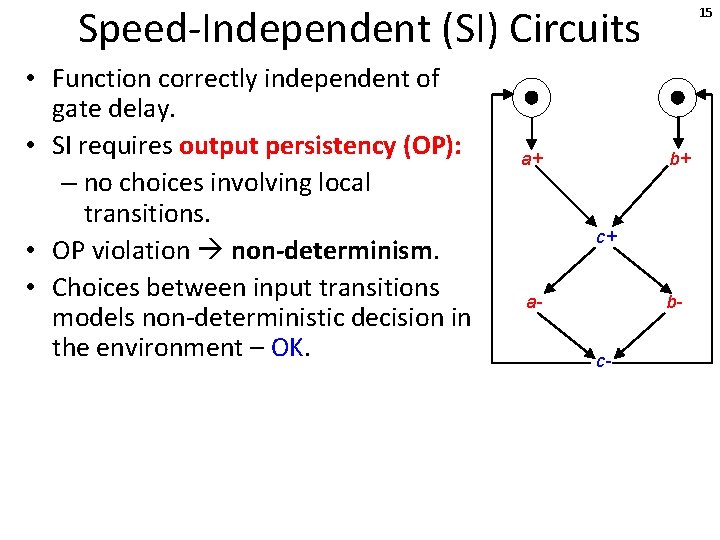
Speed-Independent (SI) Circuits • Function correctly independent of gate delay. • SI requires output persistency (OP): – no choices involving local transitions. • OP violation non-determinism. • Choices between input transitions models non-deterministic decision in the environment – OK. a+ 15 b+ c+ a- bc-

Speed-Independent (SI) Circuits • Function correctly independent of gate delay. • SI requires output persistency (OP): – no choices involving local transitions. • OP violation non-determinism. • Choices between input transitions models non-deterministic decision in the environment – OK. a+ 16 b+ c+ a- bc- Speed-independent (SI) in specified environment

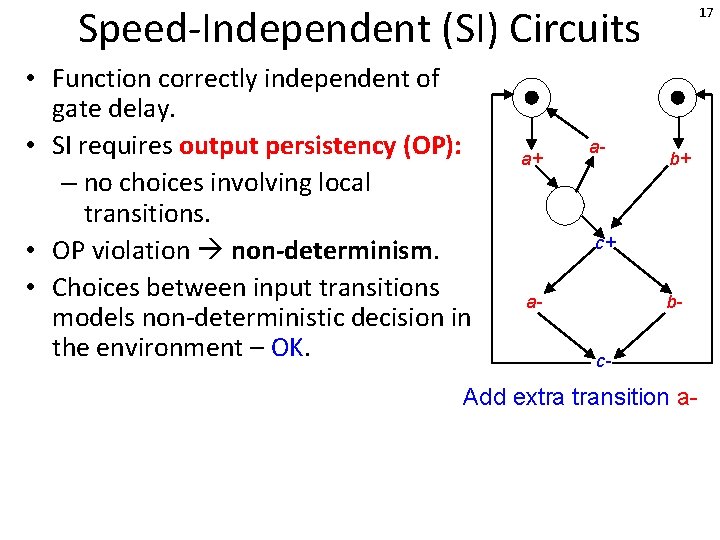
Speed-Independent (SI) Circuits • Function correctly independent of gate delay. • SI requires output persistency (OP): – no choices involving local transitions. • OP violation non-determinism. • Choices between input transitions models non-deterministic decision in the environment – OK. a+ a- 17 b+ c+ a- bc- Add extra transition a-

Speed-Independent (SI) Circuits • Function correctly independent of gate delay. • SI requires output persistency (OP): – no choices involving local transitions. • OP violation non-determinism. • Choices between input transitions models non-deterministic decision in the environment – OK. a+ a- 18 b+ c+ a- bc- Not SI: c+ disabled by a-

Speed-Independent (SI) Circuits • Function correctly independent of gate delay. • SI requires output persistency (OP): – no choices involving local transitions. • OP violation non-determinism. • Choices between input transitions models non-deterministic decision in the environment – OK. • Exception: choices involving only local transitions can be left in model: – should be documented; – if represent stochastic phenomenon, can be handled in SI manner with arbiters. a+ a- 19 b+ c+ a- bc-

Approach Overview Identify OP violations (auto) 20 PN analysis tools (auto) BN STG User assumptions (priorities) SI Circuit STG analysis tools

Refinement Approach a- 21 a+ [c] = ab + c(a + b) c+ b+ b- c-

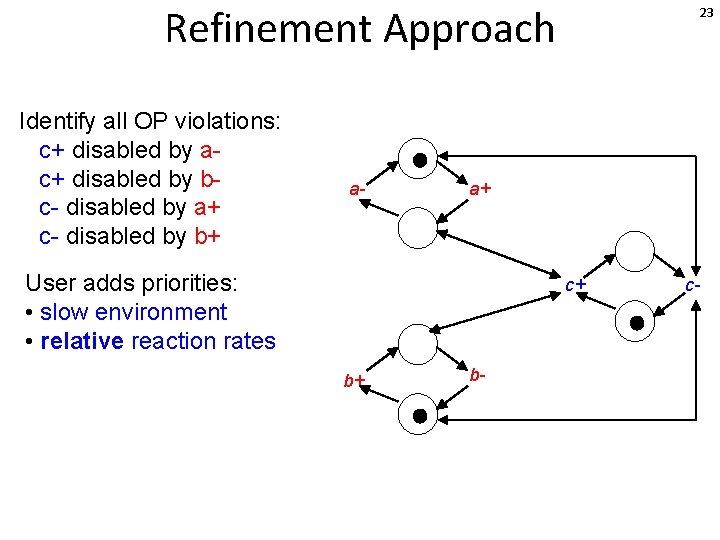
Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- 22 a+ c+ b+ b- c-

Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- 23 a+ User adds priorities: • slow environment • relative reaction rates c+ b+ b- c-

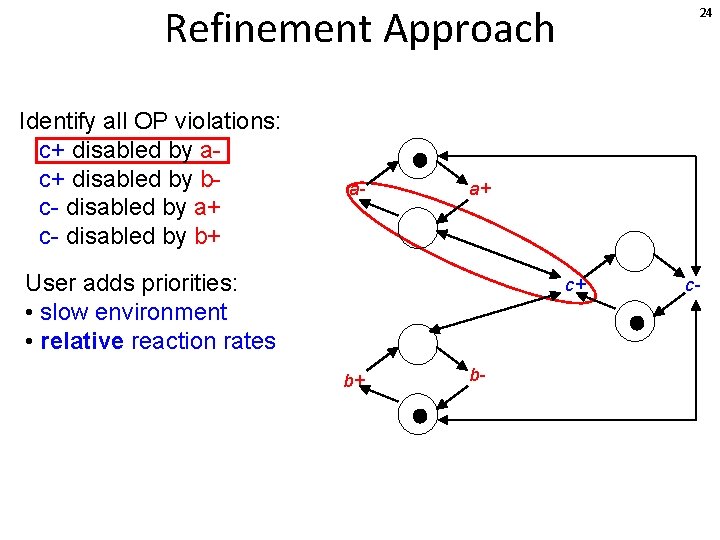
Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- 24 a+ User adds priorities: • slow environment • relative reaction rates c+ b+ b- c-

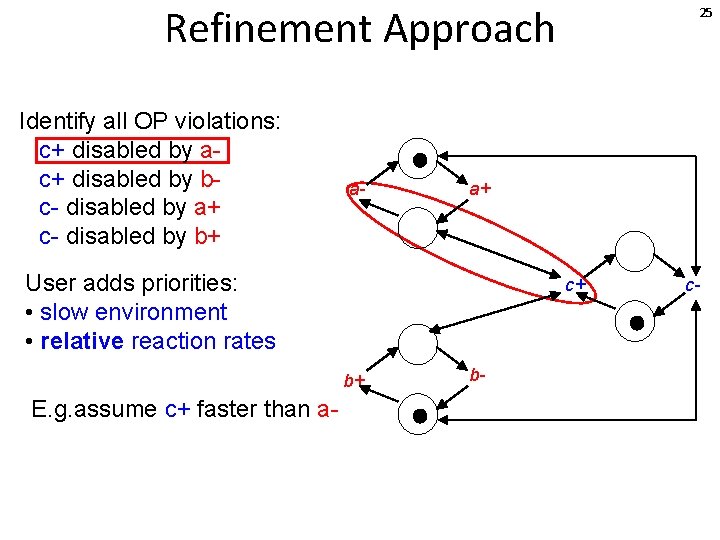
Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- a+ User adds priorities: • slow environment • relative reaction rates c+ b+ E. g. assume c+ faster than a- 25 b- c-

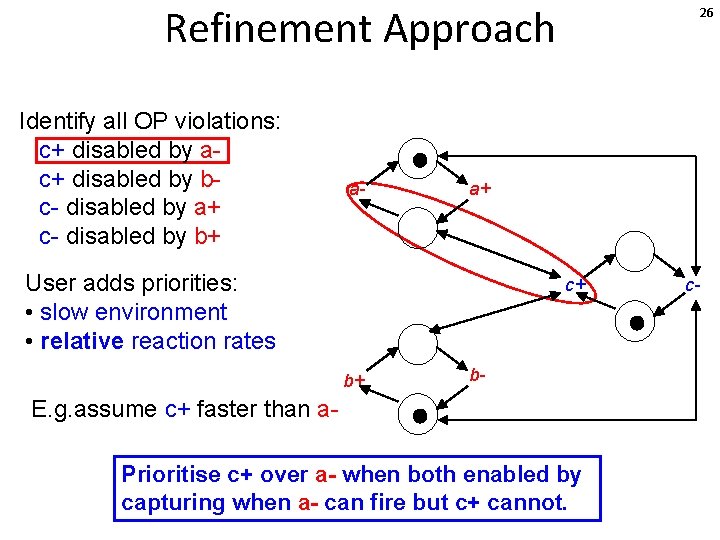
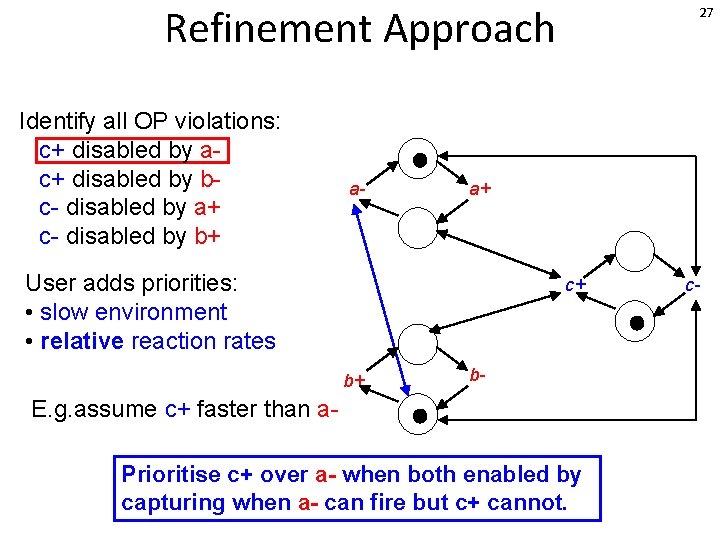
Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- 26 a+ User adds priorities: • slow environment • relative reaction rates c+ b+ b- E. g. assume c+ faster than a. Prioritise c+ over a- when both enabled by capturing when a- can fire but c+ cannot. c-

Refinement Approach Identify all OP violations: c+ disabled by ac+ disabled by bc- disabled by a+ c- disabled by b+ a- 27 a+ User adds priorities: • slow environment • relative reaction rates c+ b+ b- E. g. assume c+ faster than a. Prioritise c+ over a- when both enabled by capturing when a- can fire but c+ cannot. c-

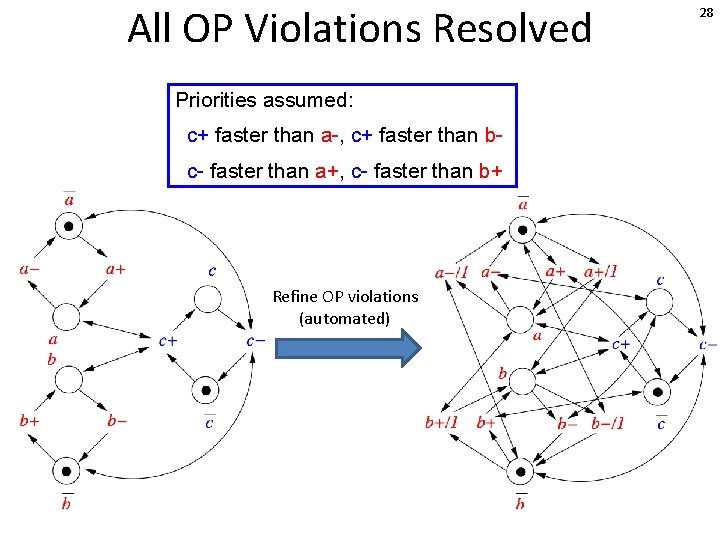
All OP Violations Resolved Priorities assumed: c+ faster than a-, c+ faster than bc- faster than a+, c- faster than b+ Refine OP violations (automated) 28

Resynthesized STG 29 ca- ba+ b-/2 b+ a-/2 a-/1 b+/1 a+/2 b-/1 b+/2 c+ • Optimised using circuit synthesis tool Petrify. • STG is SI and, surprisingly, contains more behaviour than original, i. e. can cope with more demanding environment than one intended.

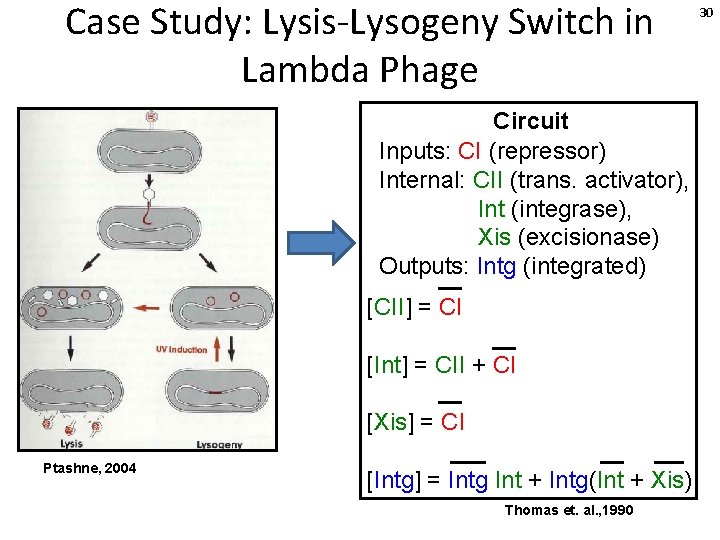
Case Study: Lysis-Lysogeny Switch in Lambda Phage Circuit Inputs: CI (repressor) Internal: CII (trans. activator), Int (integrase), Xis (excisionase) Outputs: Intg (integrated) [CII] = CI [Int] = CII + CI [Xis] = CI Ptashne, 2004 [Intg] = Intg Int + Intg(Int + Xis) Thomas et. al. , 1990 30

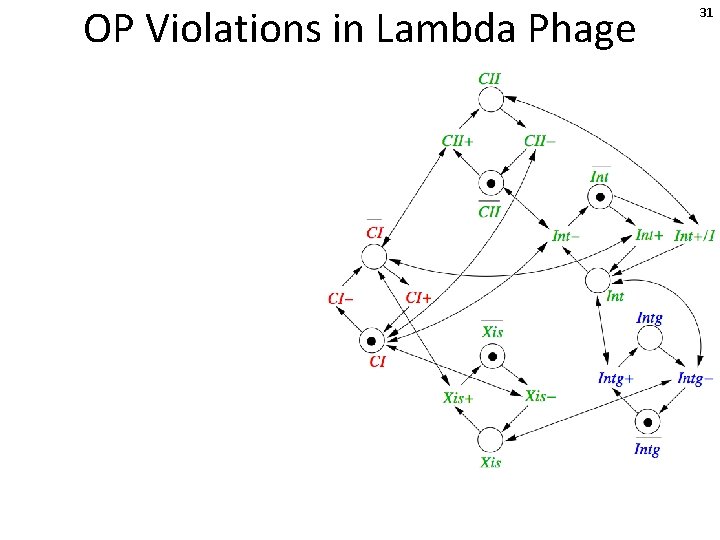
OP Violations in Lambda Phage 31

OP Violations in Lambda Phage OP violations: Xis+ disabled by CI+ Xis− disabled by CI− Int+ disabled by CI + Int− disabled by CI − CII+ disabled by CI+ CII − disabled by CI− Intg− disabled by Int− Intg− disabled by Xis− Intg+ disabled by Int− Int+/1 disabled by CII− 32

OP Violations in Lambda Phage Environment OP violations: Xis+ disabled by CI+ Xis− disabled by CI− Int+ disabled by CI + Int− disabled by CI − CII+ disabled by CI+ CII − disabled by CI− Intg− disabled by Int− Intg− disabled by Xis− Intg+ disabled by Int− Int+/1 disabled by CII− 33

OP Violations in Lambda Phage Environment OP violations: Xis+ disabled by CI+ Xis− disabled by CI− Int+ disabled by CI + Int− disabled by CI − CII+ disabled by CI+ CII − disabled by CI− Intg− disabled by Int− Intg− disabled by Xis− Intg+ disabled by Int− Int+/1 disabled by CII− Resolve by assuming slow environment 34

OP Violations in Lambda Phage Environment OP violations: Xis+ disabled by CI+ Xis− disabled by CI− Int+ disabled by CI + Int− disabled by CI − CII+ disabled by CI+ CII − disabled by CI− Intg− disabled by Int− Intg− disabled by Xis− Intg+ disabled by Int− Int+/1 disabled by CII− Resolve by assuming slow environment 35

Final SI STG • Much less cluttered. • Remaining OP violations: Intg− disabled by Int− Intg− disabled by Xis− Intg+ disabled by Int− Heart of lysis-lysogeny switch (stochastic) • Can now be analysed further with PN and STG tools. 36

Conclusions 37 • BN STG SI STG. • Framework for obtaining realistic models of GRNs using notion of SI circuits: – refine unrealisable behaviour based on user knowledge; – identifying and documenting missing information. • • STG construction and refinement automated. Re-use existing PN and STG tools/techniques for analysis. Not all OP violations may always be resolved document. Future work: – further case studies; – generalise approach to multi-valued networks; – investigate application to synthetic biology.

Thanks A Case for Using Signal Transition Graphs for Analysing and Refining Genetic Network Richard Banks, Victor Khomenko and Jason Steggles http: //bioinf. ncl. ac. uk/gnapn/ 38