1 8 Inverse Functions Consider the graphs of

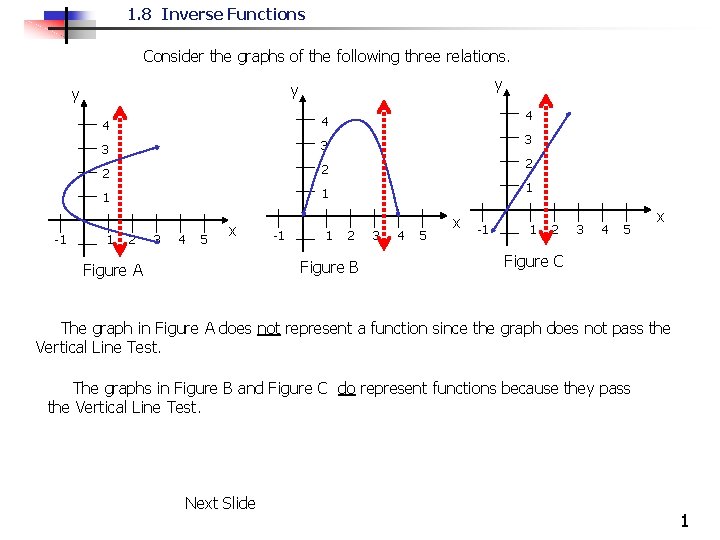
1. 8 Inverse Functions Consider the graphs of the following three relations. -1 y y y 4 4 3 3 2 2 1 1 1 2 3 4 5 x -1 1 4 3 2 1 2 Figure B Figure A 3 4 5 x -1 1 2 3 4 5 x Figure C The graph in Figure A does not represent a function since the graph does not pass the Vertical Line Test. The graphs in Figure B and Figure C do represent functions because they pass the Vertical Line Test. Next Slide 1

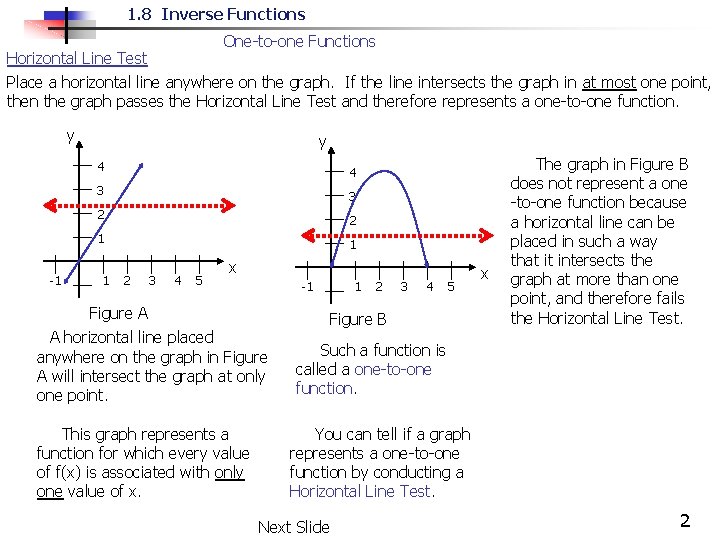
1. 8 Inverse Functions One-to-one Functions Horizontal Line Test Place a horizontal line anywhere on the graph. If the line intersects the graph in at most one point, then the graph passes the Horizontal Line Test and therefore represents a one-to-one function. y y 4 4 3 3 2 2 1 -1 1 1 2 3 4 5 x -1 Figure A A horizontal line placed anywhere on the graph in Figure A will intersect the graph at only one point. This graph represents a function for which every value of f(x) is associated with only one value of x. 1 2 3 4 5 Figure B x The graph in Figure B does not represent a one -to-one function because a horizontal line can be placed in such a way that it intersects the graph at more than one point, and therefore fails the Horizontal Line Test. Such a function is called a one-to-one function. You can tell if a graph represents a one-to-one function by conducting a Horizontal Line Test. Next Slide 2

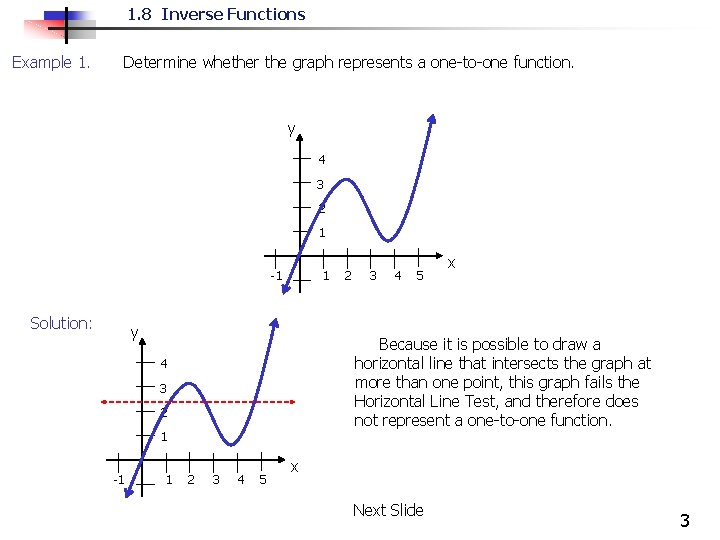
1. 8 Inverse Functions Example 1. Determine whether the graph represents a one-to-one function. y 4 3 2 1 -1 Solution: 1 y 3 2 1 1 3 4 5 x Because it is possible to draw a horizontal line that intersects the graph at more than one point, this graph fails the Horizontal Line Test, and therefore does not represent a one-to-one function. 4 -1 2 2 3 4 5 x Next Slide 3

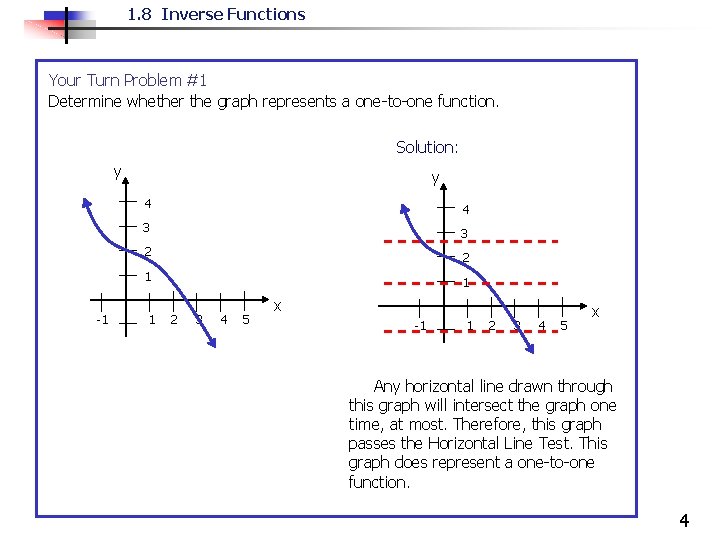
1. 8 Inverse Functions Your Turn Problem #1 Determine whether the graph represents a one-to-one function. Solution: y -1 y 4 4 3 3 2 2 1 1 1 2 3 4 5 x -1 1 2 3 4 5 x Any horizontal line drawn through this graph will intersect the graph one time, at most. Therefore, this graph passes the Horizontal Line Test. This graph does represent a one-to-one function. 4

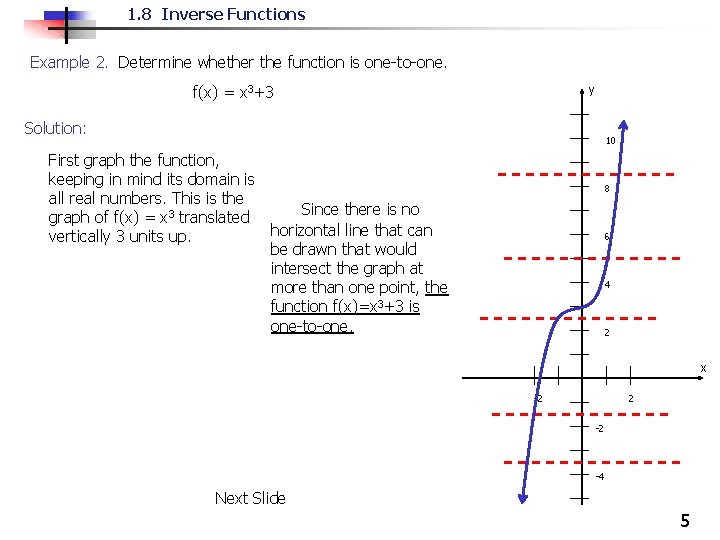
1. 8 Inverse Functions Example 2. Determine whether the function is one-to-one. f(x) = x 3+3 y Solution: 10 First graph the function, keeping in mind its domain is all real numbers. This is the Since there is no graph of f(x) = x 3 translated horizontal line that can vertically 3 units up. be drawn that would intersect the graph at more than one point, the function f(x)=x 3+3 is one-to-one. 8 6 4 2 x -2 2 -2 -4 Next Slide 5

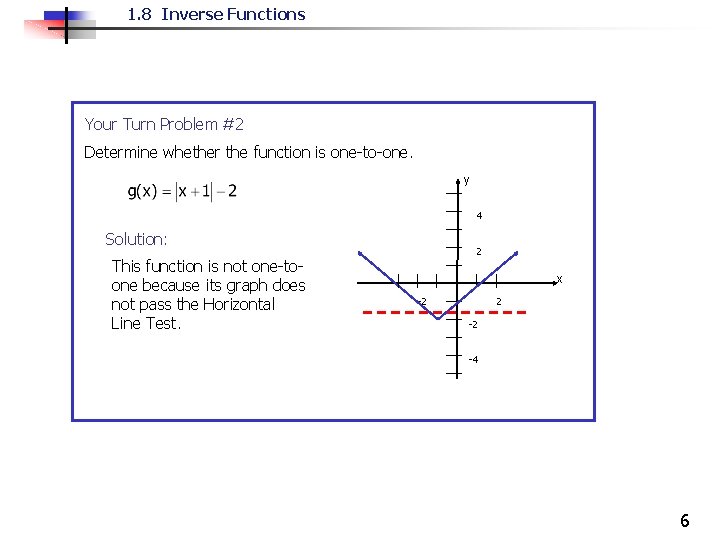
1. 8 Inverse Functions Your Turn Problem #2 Determine whether the function is one-to-one. y 4 Solution: This function is not one-toone because its graph does not pass the Horizontal Line Test. 2 x -2 2 -2 -4 6

1. 8 Inverse Functions Now that we have introduced one-to-one functions, we can discuss inverse functions. Two functions, f and g, are inverses of each other if the following two statements hold true: and The values in the domain of function f will be the same as the values in the range of function g. Also, the values in the range of function f will be the same as the values in the domain of function g. You might say that two functions are inverses of each other if they undo the effects of each other. Only functions that are one-to-one have inverse functions. When a function is not one-to-one, it is possible to place restrictions on the function’s domain in order to generate a function that is one-to-one. Next Slide 7

1. 8 Inverse Functions Example 3. Verify that the functions are inverses of each other: Solution: Note that the domain of f (all real numbers) is also the range of g. Similarly, the range of f (all real numbers) is also the domain of g. Your Turn Problem #3 Solution: 8

1. 8 Inverse Functions The symbol that indicates a function is an inverse of an original function f is “f -1” is read aloud as “ f inverse” or “the inverse of f”. Do not think of “f -1” as the reciprocal of f. “f -1” is not “f” raised to the negative one power. If you think of a function as a set of ordered pairs for which the first element is never repeated, then a one-to-one function can be thought of as a set of ordered pairs that has an extra restriction in that the second element is never repeated. So if g is defined to be a function composed of the ordered pairs (3, 9), (5, 7), and (2, 1), then g – 1 would be the inverse function of g and would have (9, 3), (7, 5), and (1, 2) as its ordered pairs. Note that the domain of g, the x-values 3, 5, and 2, are the same y-values in the range of g – 1. The range of g has the same values as the domain of g – 1. Next Slide 9

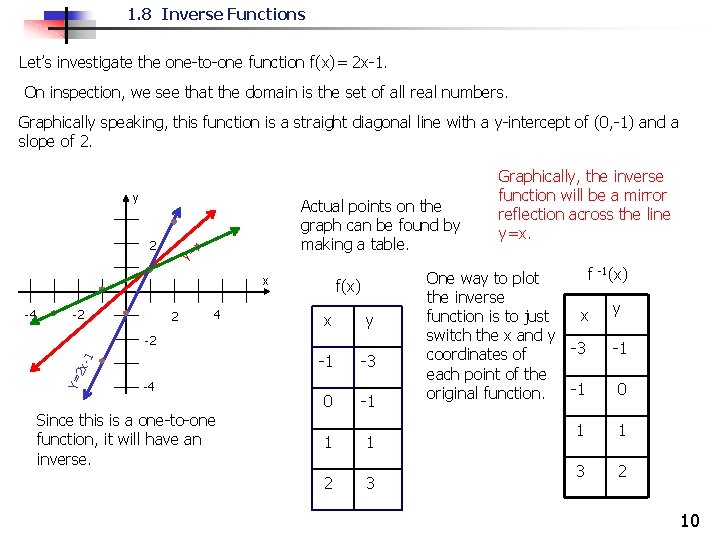
1. 8 Inverse Functions Let’s investigate the one-to-one function f(x)= 2 x-1. On inspection, we see that the domain is the set of all real numbers. Graphically speaking, this function is a straight diagonal line with a y-intercept of (0, -1) and a slope of 2. y 2 y= Actual points on the graph can be found by making a table. x x -2 2 4 x y -1 -3 0 -1 2 x- 1 -2 Y= -4 f(x) -4 Since this is a one-to-one function, it will have an inverse. 1 1 2 3 Graphically, the inverse function will be a mirror reflection across the line y=x. f -1(x) One way to plot the inverse y x function is to just switch the x and y -3 -1 coordinates of each point of the -1 0 original function. 1 1 3 2 10

1. 8 Inverse Functions One of the last things we need to do is come up with a procedure for finding the equation of inverse functions, if we are initially given a one-to-one function. Procedure for finding an Inverse Function Step 1: Replace “f(x)” with “y”. Step 2: Switch “x” and “y”. Step 3: Solve for “y”. Step 4: Replace “y” with “f -1(x)’’. Example 4. If f(x)=6 x-11, find f-1(x). Solution: Step 1: Replace “f(x)” with “y”. Step 2: Switch “x” and “y”. Step 3: Solve for “y”. Step 4: Replace “y” with “f-1(x)”. Your Turn Problem #4 If g(x)=4 x+31, find Find g-1(x). Answer: or 11