1 7 Solve Absolute Value Equations and Inequalities

1. 7 – Solve Absolute Value Equations and Inequalities Recall that the absolute value of a number x, written |x|, is the distance the number is from 0 on a number line. This understanding of absolute value can be extended to apply to simple absolute value equations.

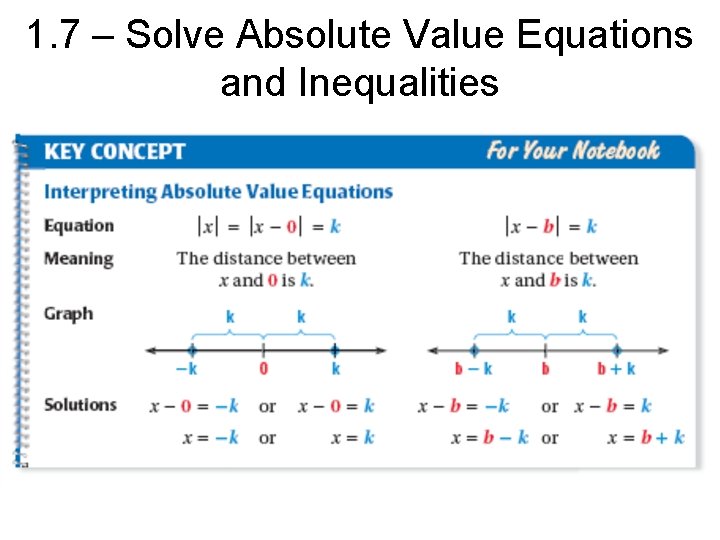
1. 7 – Solve Absolute Value Equations and Inequalities

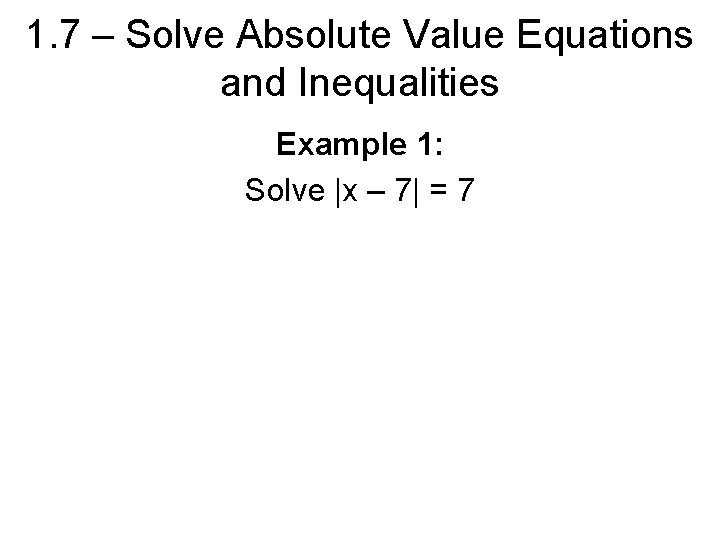
1. 7 – Solve Absolute Value Equations and Inequalities Example 1: Solve |x – 7| = 7

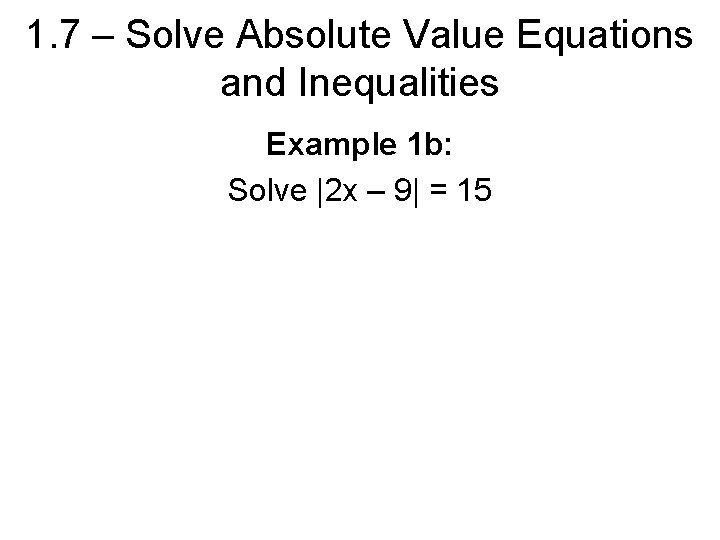
1. 7 – Solve Absolute Value Equations and Inequalities Example 1 b: Solve |2 x – 9| = 15

1. 7 – Solve Absolute Value Equations and Inequalities

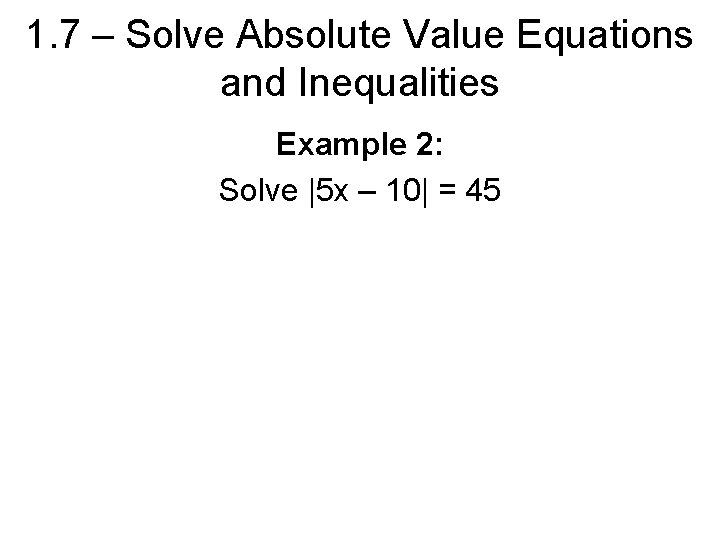
1. 7 – Solve Absolute Value Equations and Inequalities Example 2: Solve |5 x – 10| = 45

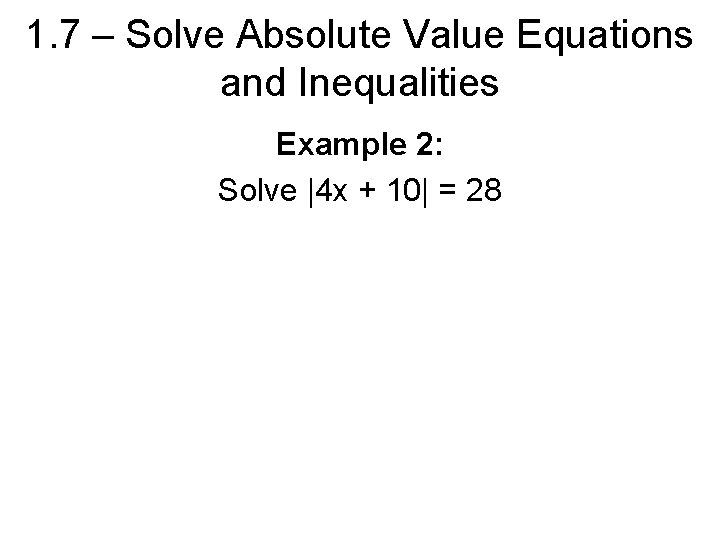
1. 7 – Solve Absolute Value Equations and Inequalities Example 2: Solve |4 x + 10| = 28

1. 7 – Solve Absolute Value Equations and Inequalities Extraneous Solutions: When you solve an absolute value equation, it is possible for a solution to be extraneous. An extraneous solution is an apparent solution that must be rejected because it does not satisfy the original equation.

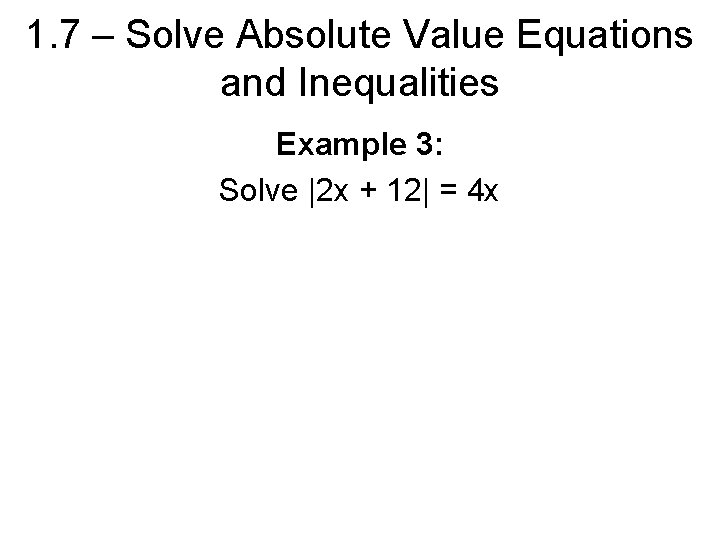
1. 7 – Solve Absolute Value Equations and Inequalities Example 3: Solve |2 x + 12| = 4 x

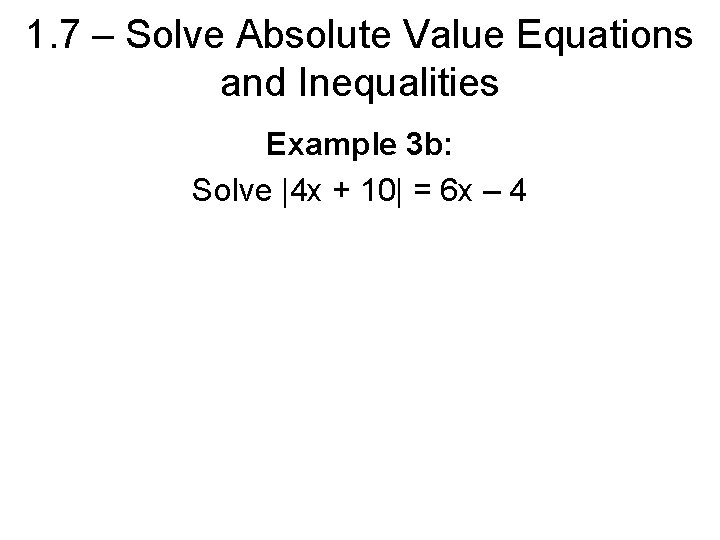
1. 7 – Solve Absolute Value Equations and Inequalities Example 3 b: Solve |4 x + 10| = 6 x – 4

1. 7 – Solve Absolute Value Equations and Inequalities

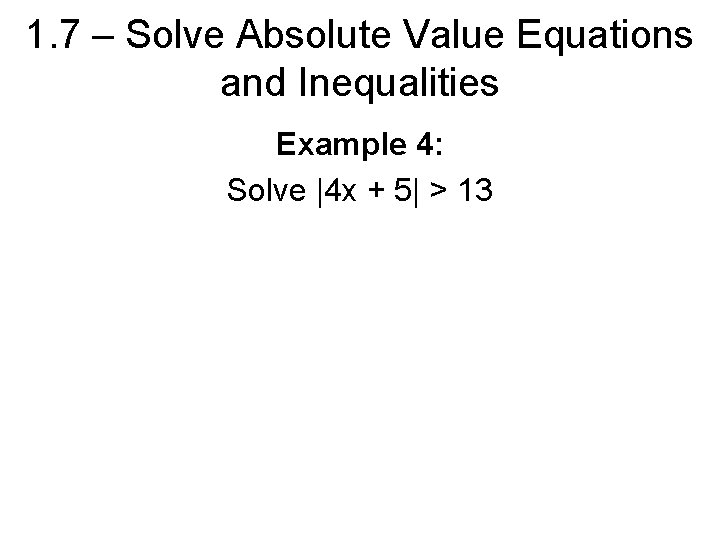
1. 7 – Solve Absolute Value Equations and Inequalities Example 4: Solve |4 x + 5| > 13

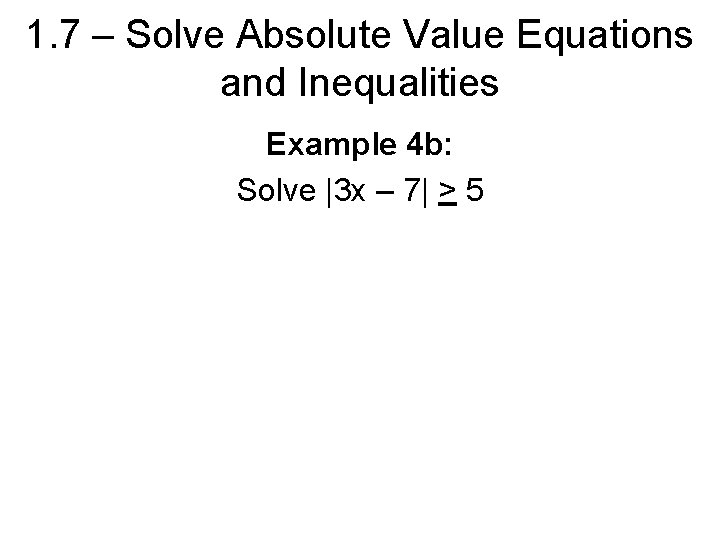
1. 7 – Solve Absolute Value Equations and Inequalities Example 4 b: Solve |3 x – 7| > 5