1 6 B Distributive Property and Combine Like

1 -6 B Distributive Property and Combine Like Terms – Evaluate Algebraic Expressions Algebra 1 Glencoe Mc. Graw-Hill Linda Stamper

Do not use a calculator to complete homework. Students who are calculator dependent tend to make more calculating errors on tests. After you finish an odd homework problem check the answer in the back of the book. If the answer is incorrect, investigate why it is wrong. When students find their errors right away it is more effective. Don’t skip steps. Write out the support work so your eyes can see what your brain needs to calculate. “I did it in my head” often leads to errors. Take notes in class, read the related lesson in the text, and then review, review. It’s just not enough to sit in class for 45 minutes and then hope you have absorbed it all. Study tips

A common error in distributing occurs when a negative is involved with subtraction. To avoid errors change subtraction to addition. The problem. – 3(m - 5) Change subtraction to addition. – 3(m +–– 5) – – 3 m + 3(– 5) Distribute. Simplify. – 3 m + 15

Rewrite using the distributive property. Then simplify. Example 1 – 8(m - 9) – 8(m +–– 9) – – 8 m + 8(– 9) – 8 m + 72 Example 2 (3 g - 8)(– 5) (3 g +–– 8)(– 5) – 3 g(– 5) + 8(– 5) – 15 g + 40 Example 3 – 8(x - 2 y + 3 z) – 8(x +– – 2 y + 3 z) – 8 x + – 8(– 2 y) + – 8(3 z) – 8 x + 16 y + – 24 z – 8 x + 16 y – 24 z Note: Your answer must be simplified. Undo the double signs.

Rewrite using the distributive property. Then simplify. The problem. Change subtraction to addition. Give the negative sign a multiplier of 1. 1 + 7 y + 25 Simplify. What property justifies this step? Copy in your spiral notebook!

Rewrite using the distributive property. Then simplify. Example 4 –(– 2 x - 15) – – 15) – 1(– 2 x + (– 1)– 2 x + (– 1)(– 15) Example 5 – (m - 7) – 1(m +–– 7) – 1(m) + (– 1)(– 7) –m + 7 2 x + 15 Good form Use good form! gives the Do not write variable term as -1 m + 7. before the constant! Example 6 – (6 - y) – 1(6+–– y) – 1(6) + (– 1)(–y) – 6 + y What property justifies this move?

Simplify the expression. An expression is simplified if it has: no grouping symbols, no like terms, and no double signs. Like terms are terms in an expression that have the same variable raised to the same power. In the answer, good form is alphabetical, descending order! Constants are last.

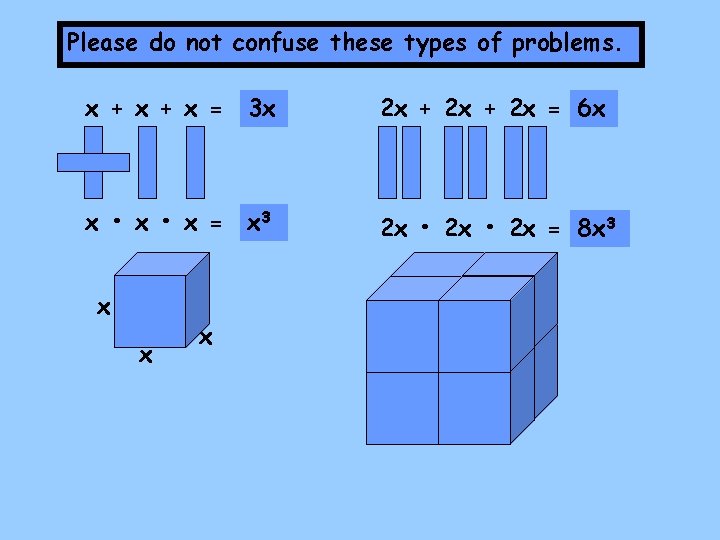
Please do not confuse these types of problems. x + x = 3 x 2 x + 2 x = 6 x x • x = x 3 2 x • 2 x = 8 x 3 x x x

Simplify the expression. Write problem. Change subtraction to addition. Combine like terms. 5 x 2 + – – 7 x + 3 x 2 + 5 x Undo the double signs. 8 x 2 – 2 x Good form is alphabetical descending order! Constants are last. 8 x 2 + – 2 x 8 x 2 +(– 2 x)

Simplify the expression. Example 7 Example 8 Example 9 4 y - (6 y - 9) Example 10 a - b(b - 2 a) + 4 b 2 3(y + 6) + 5(4 - y) + 7 y 2

Simplify the expression. Example 8 Example 7 3(y + 6) + 5(4 - y) + 7 y 2 3 x 2 +–– 5 x + 4 x 2 –+– 7 x 7 x 2 + – 12 x 7 x 2 – 12 x 3(y + 6) + 5(4 +– – y) + 7 y 2 3(y) + 3(6) + 5(4) + 5(-y) + 7 y 2 3 y +18 +20 + – 5 y + 7 y 2 – 2 y + 38 Good form has the variables in alphabetical order with the powers in descending order! Constants are last.

Simplify the expression. Example 9 Example 10 a - b(b - 2 a) + 4 b 2 4 y - (6 y - 9) 4 y +–– 1(6 y +– – 9) 4 y + (-1)(6 y) + (-1)(-9) 4 y + – 6 y + 9 a +–– b(b +–– 2 a) + 4 b 2 a + (-b)(b) + (-b)(-2 a) + 4 b 2 a + – b 2 + 2 ab + 4 b 2 a + 2 ab + 3 b 2 – 2 y + 9 Distribute the Good form is negative one. alphabetical descending order!

Evaluating Algebraic Expressions An algebraic expression is easier to evaluate when it is simplified Simplify by using the distributive property and then combine like terms. Then use the value given to evaluate.

Simplify and then evaluate when x = – 2. Write the problem. – 5 x(2 - 3 x) + 7 x Change subtraction to addition. – 5 x(2+–– 3 x) + 7 x Distribute. Combine like terms. Substitute (don’t forget to use parentheses). Simplify. – 10 x + 15 x 2 + 7 x 15 x 2 + – 3 x 15(– 2)2 + – 3(– 2) 15(4) + (– 3)(– 2) 60 + 6 66

Simplify and then evaluate. Example 11 when x = 2 – x(8 - x) + 2 x – x(8 –+– x) + 2 x – 8 x + x 2 + 2 x x 2 + – 6 x (2)2 + – 6(2) 4 + – 12 – 8 Example 12 when x = 4 6(-x - 3) - x(9 + x) 6(– x +–– 3) +–– x(9 + x) – 6 x + – 18 + – 9 x + –x 2 – x 2 + – 15 x + – 18 – (4)2 + – 15(4) + – 18 – 16 + – 60 + – 18 – 76 + – 18 – 94

1 -A 11 Handout A 11