1 6 3 Graphing Linear Relations The graph

1 6 -3 Graphing Linear Relations The graph of an equation in two variables x and y is the set of all points (x, y) whose coordinates satisfy the equation. For instance, the point (– 1, 3) is on the graph of 2 y – x = 7 because the equation is satisfied when – 1 is substituted for x and 3 is substituted for y. That is, 2 y – x = 7 Original Equation 2(3) – (– 1) = 7 Substitute for x and y. 7=7 Equation is satisfied.

6 -3 Graphing Linear Relations To sketch the graph of an equation, 1. Find several solution points of the equation by substituting various values for x and solving the equation for y. 2. Plot the points in the coordinate plane. 3. Connect the points using straight lines or smooth curves. 2

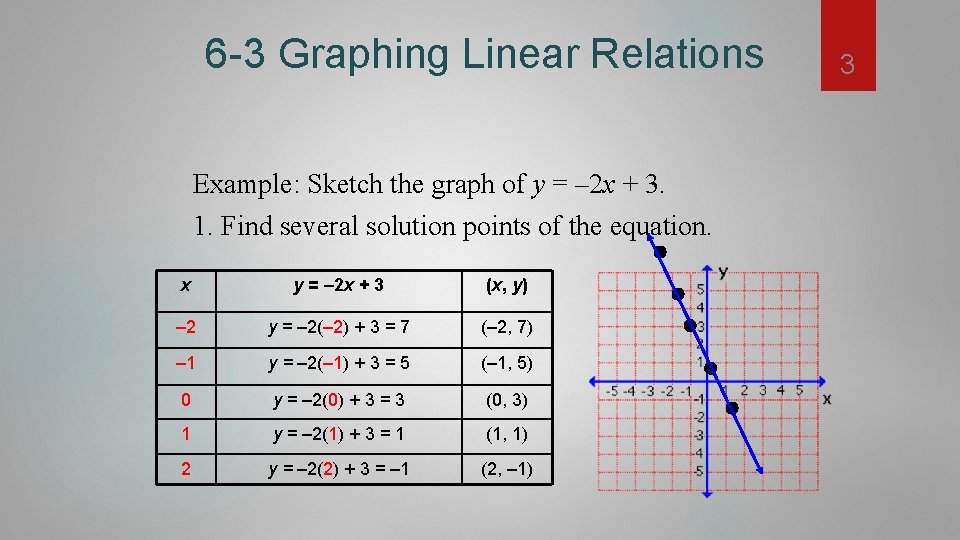
6 -3 Graphing Linear Relations Example: Sketch the graph of y = – 2 x + 3. 1. Find several solution points of the equation. x y = – 2 x + 3 (x, y) – 2 y = – 2(– 2) + 3 = 7 (– 2, 7) – 1 y = – 2(– 1) + 3 = 5 (– 1, 5) 0 y = – 2(0) + 3 = 3 (0, 3) 1 y = – 2(1) + 3 = 1 (1, 1) 2 y = – 2(2) + 3 = – 1 (2, – 1) 3

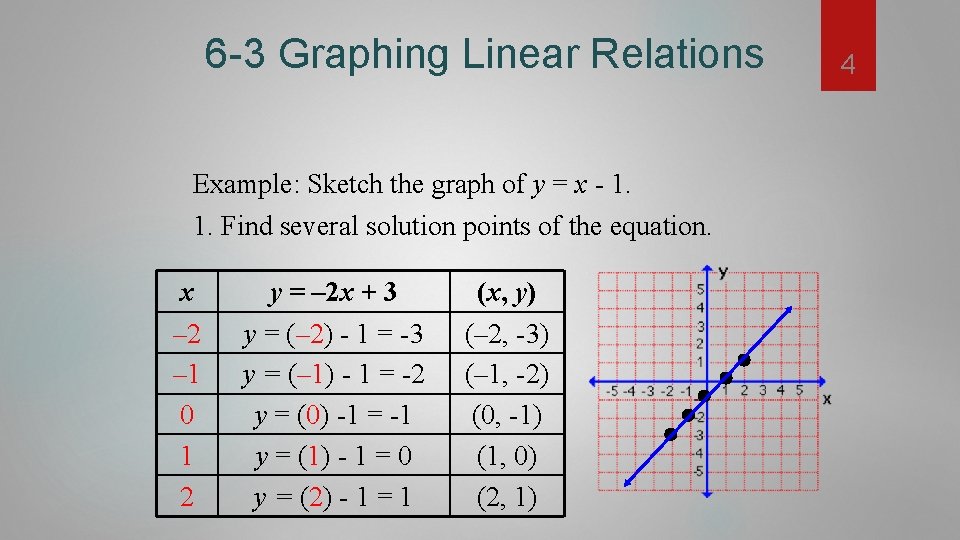
6 -3 Graphing Linear Relations Example: Sketch the graph of y = x - 1. 1. Find several solution points of the equation. x – 2 – 1 0 1 2 y = – 2 x + 3 y = (– 2) - 1 = -3 y = (– 1) - 1 = -2 y = (0) -1 = -1 y = (1) - 1 = 0 y = (2) - 1 = 1 (x, y) (– 2, -3) (– 1, -2) (0, -1) (1, 0) (2, 1) 4

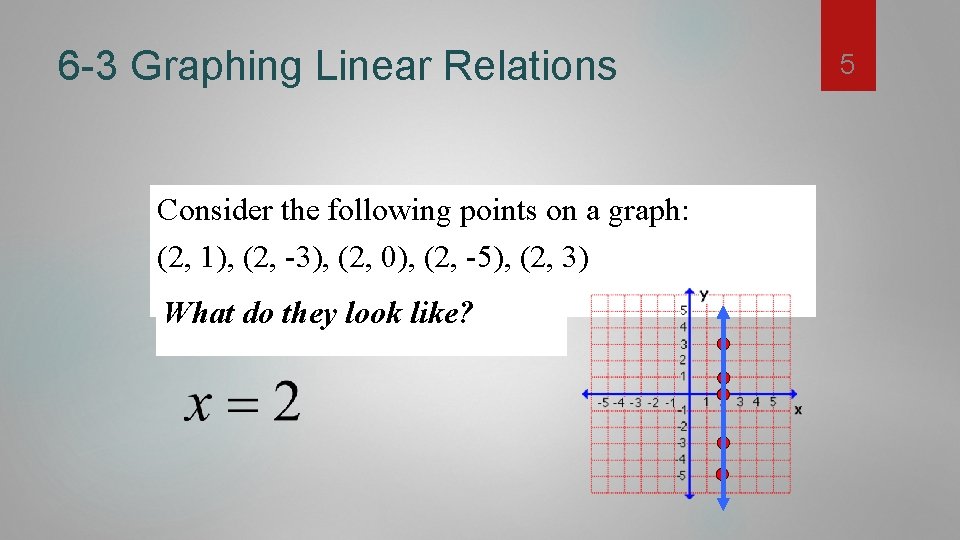
6 -3 Graphing Linear Relations Consider the following points on a graph: (2, 1), (2, -3), (2, 0), (2, -5), (2, 3) What do they look like? 5

6 -3 Graphing Linear Relations How would you graph the following equations? 6

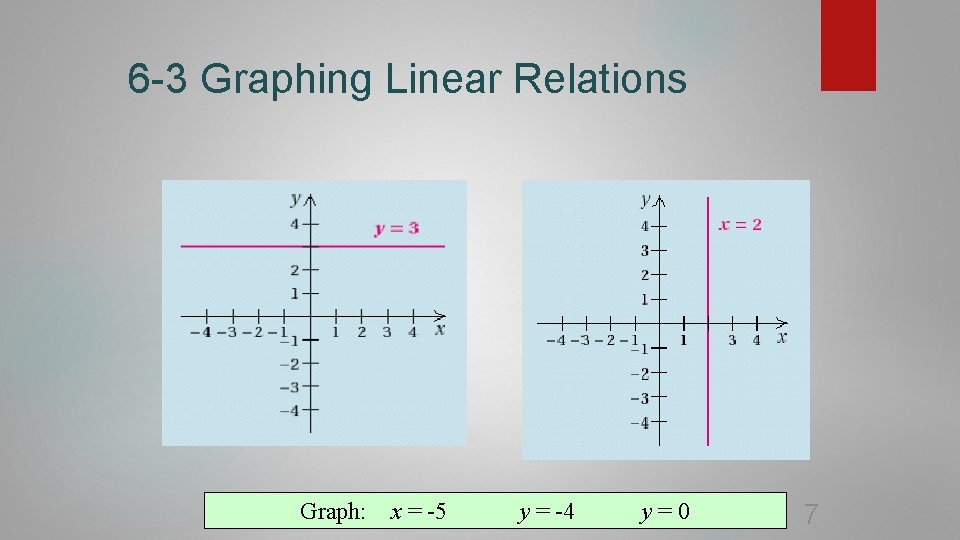
6 -3 Graphing Linear Relations Graph: x = -5 y = -4 y=0 7

8 6 -3 Graphing Linear Relations Horizontal and Vertical Lines If a is any real number: The graph of x = a is a vertical line with x-intercept (a, 0) If a is 0, ( x = 0 ) the line is the y-axis. If b is any real number: The graph of y = b is a horizontal line with y-intercept (0, b) If b is 0, ( y = 0 ) the line is the x-axis.