1 5 LINEAR MODELS Objectives 1 Algebraically fit

1. 5 LINEAR MODELS Objectives: 1. Algebraically fit a linear model. 2. Use a calculator to determine a linear model. 3. Find and interpret the correlation coefficient for a model. 4. Create and interpret a residual plot for a linear model.

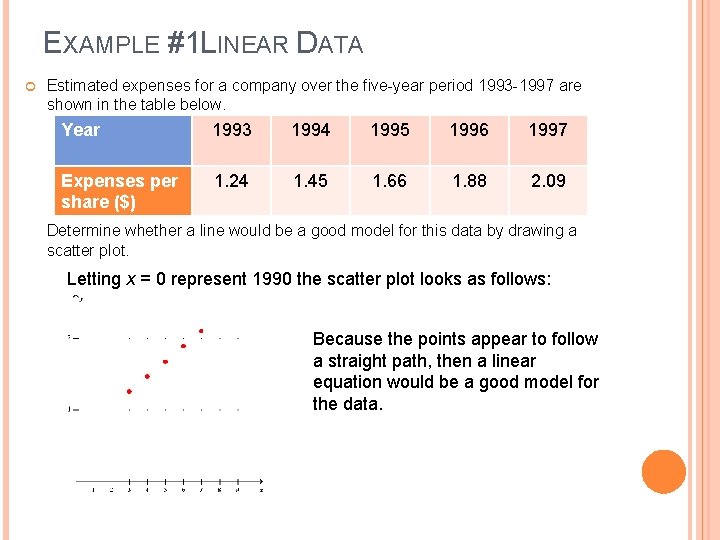
EXAMPLE #1 LINEAR DATA Estimated expenses for a company over the five-year period 1993 -1997 are shown in the table below. Year 1993 1994 1995 1996 1997 Expenses per share ($) 1. 24 1. 45 1. 66 1. 88 2. 09 Determine whether a line would be a good model for this data by drawing a scatter plot. Letting x = 0 represent 1990 the scatter plot looks as follows: Because the points appear to follow a straight path, then a linear equation would be a good model for the data.

EXAMPLE #2 MODELING DATA The data below shows the monthly amount spent on marketing (in hundreds of dollars) x and the monthly sales revenue (in thousands of dollars) r of an online store over a seven-month period. x 0 1 2 3 4 5 6 r 2 2 3 3 4 5 5 Find two models for the data, each determined by a pair of data points. For one model, use points (1, 2) and (4, 4). For the other model, use (1, 2) and (5, 5). Then use residuals to see which model best fits the data.

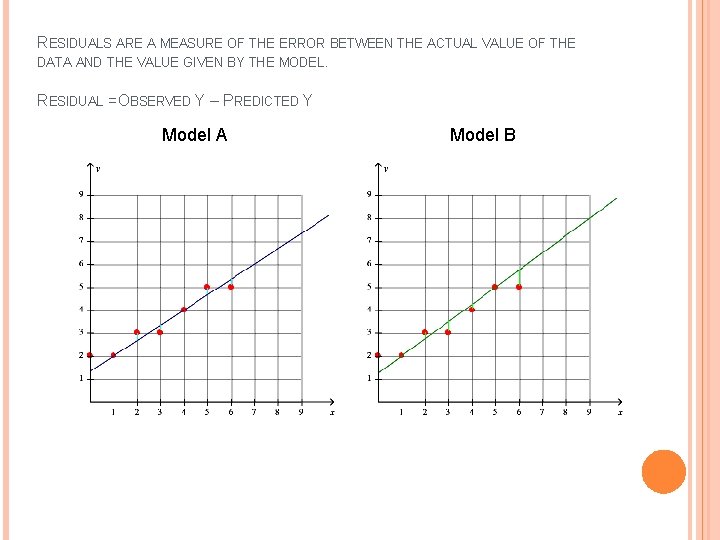
RESIDUALS ARE A MEASURE OF THE ERROR BETWEEN THE ACTUAL VALUE OF THE DATA AND THE VALUE GIVEN BY THE MODEL. RESIDUAL = OBSERVED Y – PREDICTED Y Model A Model B

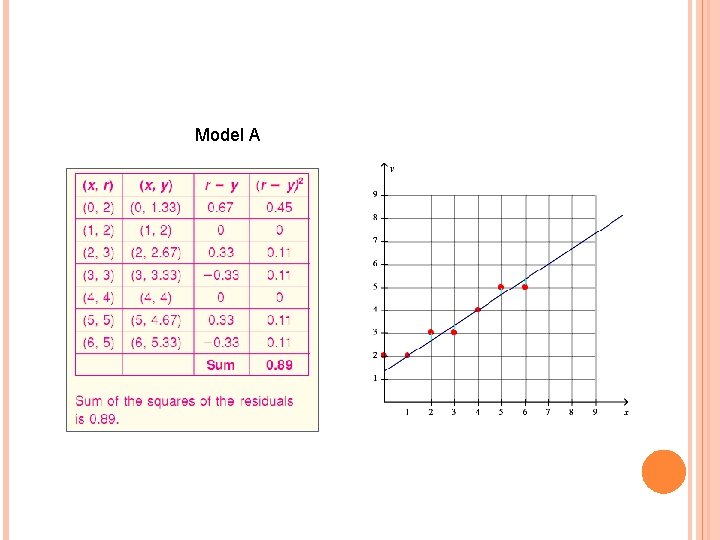
Model A

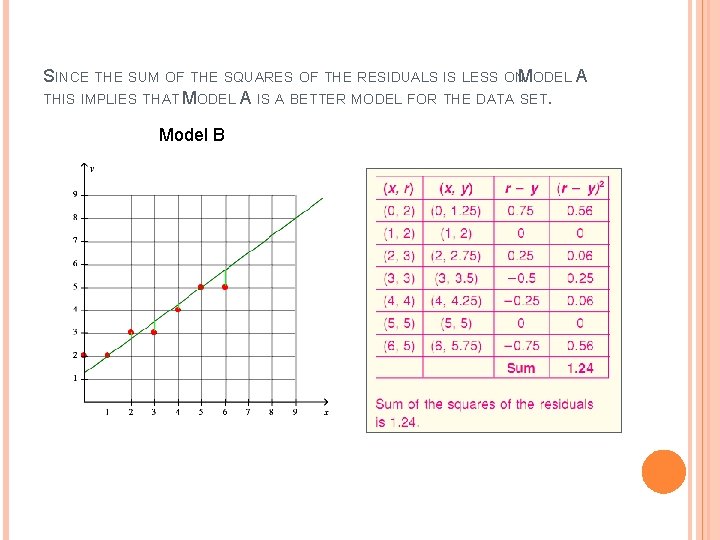
SINCE THE SUM OF THE SQUARES OF THE RESIDUALS IS LESS ONMODEL A THIS IMPLIES THAT MODEL A IS A BETTER MODEL FOR THE DATA SET. Model B

CORRELATION COEFFICIENTS When finding the Least-Squares Regression Line, an r - value is given called the correlation coefficient. This is different than the r used when calculating residuals. The correlation coefficient is always given between -1 and 1 with positive 1 being a perfect correlation in the positive direction and -1 being a perfect correlation in the negative direction. A value of 0 means now correlation at all.

EXAMPLE #3 MODELING DATA The lengths of the radii of the inscribed circles in regular polygons whose sides have length one unit are given as follows: Number of sides 3 Radius 0. 289 0. 500 0. 688 0. 866 1. 038 1. 207 1. 374 A. B. C. 4 5 6 7 8 9 Draw a scatter plot. Find the model that best fits the data using the regression feature on a calculator. What does the correlation coefficient indicate about the data?

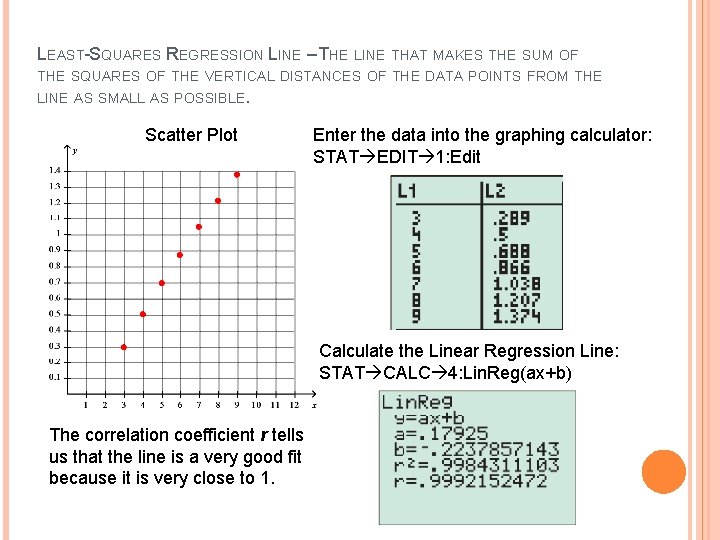
LEAST-SQUARES REGRESSION LINE – THE LINE THAT MAKES THE SUM OF THE SQUARES OF THE VERTICAL DISTANCES OF THE DATA POINTS FROM THE LINE AS SMALL AS POSSIBLE. Scatter Plot Enter the data into the graphing calculator: STAT EDIT 1: Edit Calculate the Linear Regression Line: STAT CALC 4: Lin. Reg(ax+b) The correlation coefficient r tells us that the line is a very good fit because it is very close to 1.

EXAMPLE #4 PREDICTION FROM A MODEL The total number of farms (in millions) in selected years is shown in the table below. Year 1900 1920 1930 1940 1950 1960 1970 1985 1990 Farms 5. 740 6. 518 6. 546 6. 350 5. 648 3. 963 2. 949 2. 293 2. 146 2. 196 A. Use linear regression to find an equation that models the data. Use the equation to estimate the number of farms in 1975 and in 2005. B. According to the model, when will the number of farms be one million? This implies that in the year 2017 the number of farms will reach 1 million. C. Is a line the best model for the data? Looking at the scatter plot and the r-value, a linear model doesn’t appear to be the best fit. 1995