1 5 Inverse Functions Objective To find and

1. 5 Inverse Functions Objective: To find and identify inverse functions

Definition v We defined a function as a relationship from set A to set B. An Inverse function is a relationship from set B to set A. v In other words, we switch the x and the y coordinates, and the domain and range switch.

Definition v Notice how the x and the y coordinates have switched. We can also say that the domain and range have switched.

Definition of Inverse Functions v Let f and g be functions such that v These functions are called inverse functions since they undo each other. This can also be stated

Example 1 v Find the inverse function of that . . Then verify v To find an inverse function informally, switch the x and the y and solve for y. v v

Example 1 v Find the inverse function of that . . Then verify v We will verify this fact by looking at the composition of functions.

Example 2 v Find the inverse function of

Example 3 v Find the inverse function of . (answer from previous problem) § We must first find the inverses of each function.

Example 4 v Find the inverse function of

Verifying Inverse Functions v Which of the functions is the inverse function of ?

Verifying Inverse Functions v Which of the functions is the inverse function of v So let us start with the g(x), first. (f(g(x))

Verifying Inverse Functions v Which of the functions is the inverse function of v Now we will use h(x). f(h(x))

Verify an Inverse Function v Show that functions. v f(g(x)) and are inverse g(f(x))

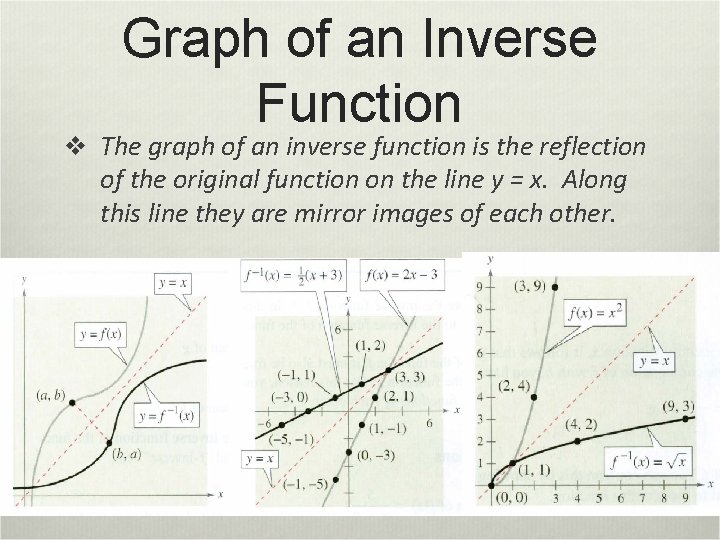
Graph of an Inverse Function v The graph of an inverse function is the reflection of the original function on the line y = x. Along this line they are mirror images of each other.

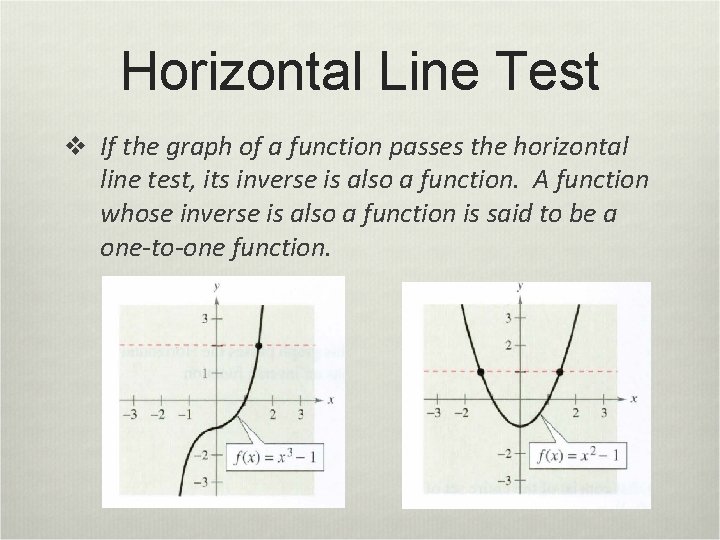
Horizontal Line Test v If the graph of a function passes the horizontal line test, its inverse is also a function. A function whose inverse is also a function is said to be a one-to-one function.

Homework v Section 1. 5 v pg 127 v #’s 5, 9, 13, 16, 17, 19, 23(a), 24(a), 29, 30, 31, 32, 33, 55, 57, 58, 63, 85, 86