1 5 Graphs of Sine and Cosine Functions



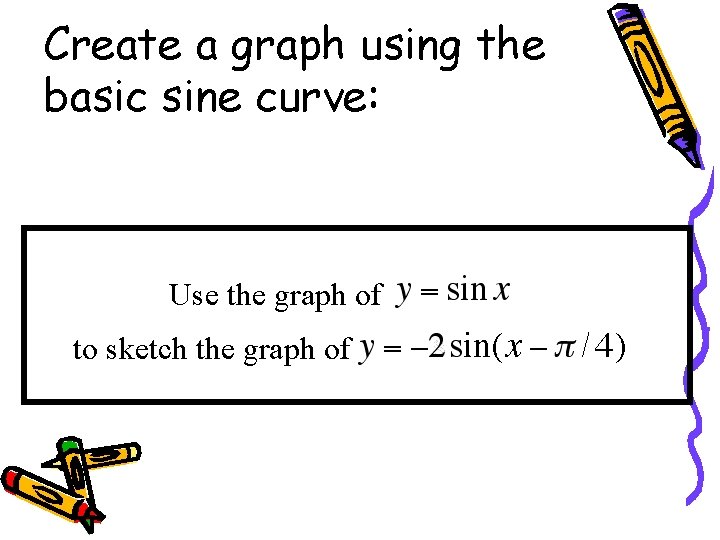
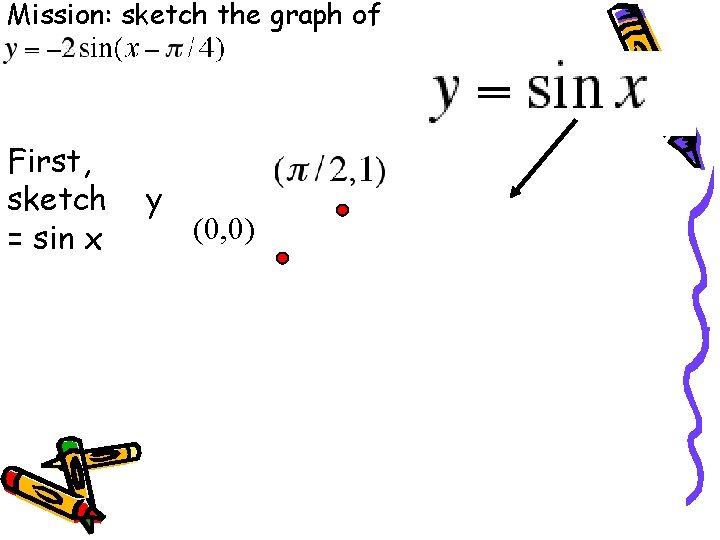
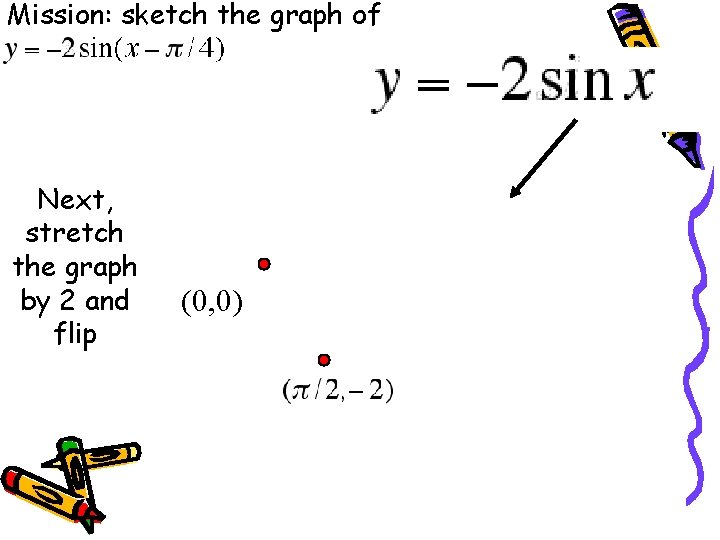
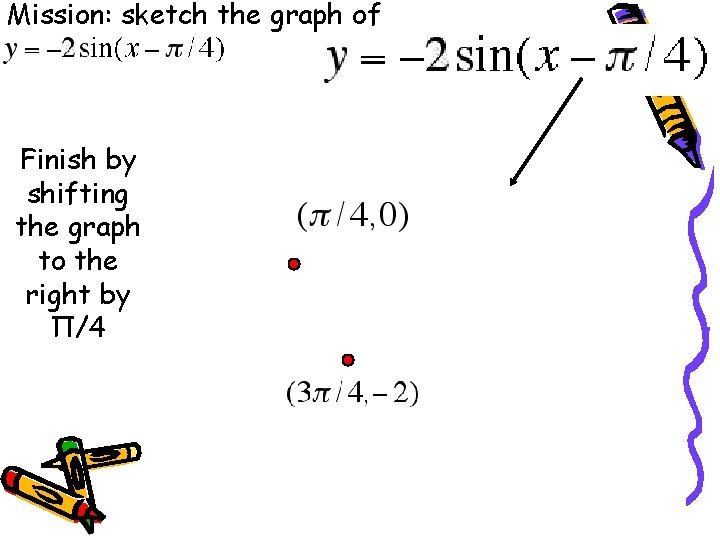



- Slides: 17

1. 5 Graphs of Sine and Cosine Functions Part 3

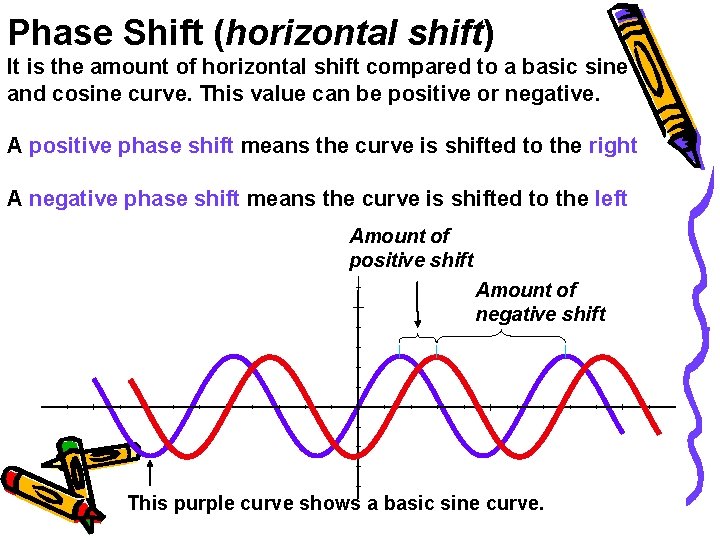
Phase Shift (horizontal shift) It is the amount of horizontal shift compared to a basic sine and cosine curve. This value can be positive or negative. A positive phase shift means the curve is shifted to the right A negative phase shift means the curve is shifted to the left Amount of positive shift Amount of negative shift This purple curve shows a basic sine curve.

What happens when we change the value of c in the general equation y = a sin(bx - c) y = a sin(b(x – c)) shifts the graph to the right by c units. y = a sin(b(x+c))shifts the graph to the left by c units. Example: If the graph of y = sin 2 x is shifted to the right by 3 units, what is the equation of the new graph? y = sin (2(x-3))

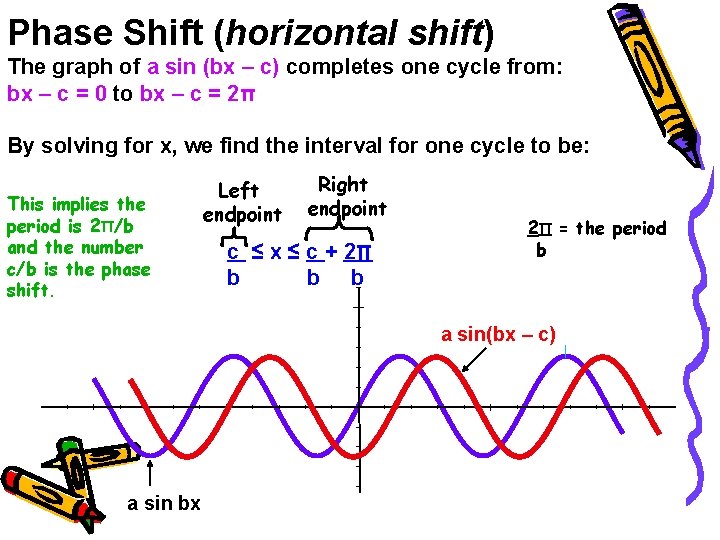
Phase Shift (horizontal shift) The graph of a sin (bx – c) completes one cycle from: bx – c = 0 to bx – c = 2Π By solving for x, we find the interval for one cycle to be: This implies the period is 2Π/b and the number c/b is the phase shift. Left endpoint Right endpoint c ≤ x ≤ c + 2Π b b b 2Π = the period b a sin(bx – c) a sin bx

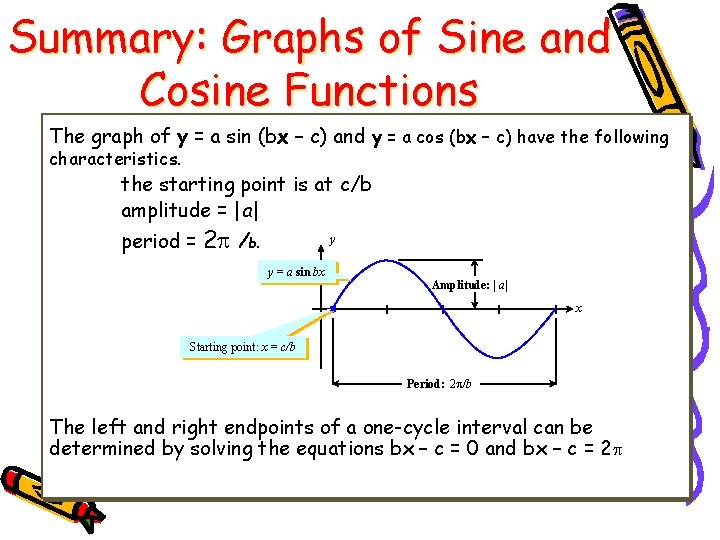
Summary: Graphs of Sine and Cosine Functions The graph of y = a sin (bx – c) and y = a cos (bx – c) have the following characteristics. the starting point is at c/b amplitude = |a| period = 2 /b. y y = a sin bx Amplitude: | a| x Starting point: x = c/b Period: 2 /b The left and right endpoints of a one-cycle interval can be determined by solving the equations bx – c = 0 and bx – c = 2

USE THE GENERAL EQUATION: y = a sin (bx – c) Example Determine the amplitude, period, and phase shift of y = 2 sin(3 x - ) Solution: Amplitude = |a| = 2 period = 2 /b = 2 /3 phase shift = c/b = /3
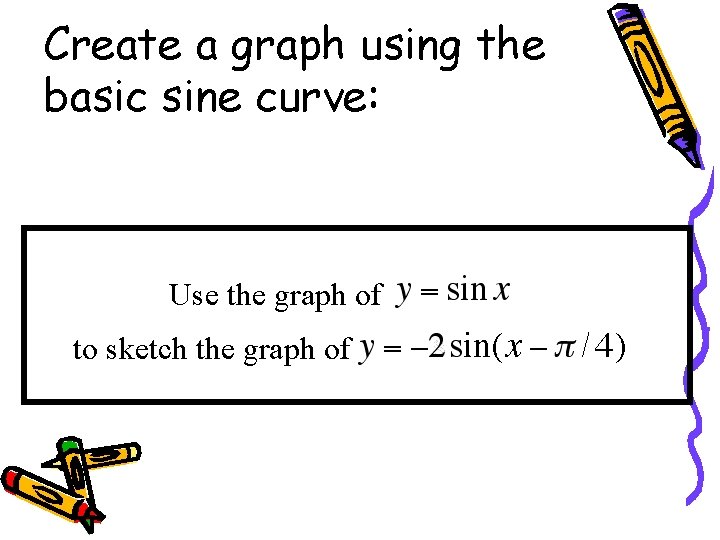
Create a graph using the basic sine curve: Use the graph of to sketch the graph of
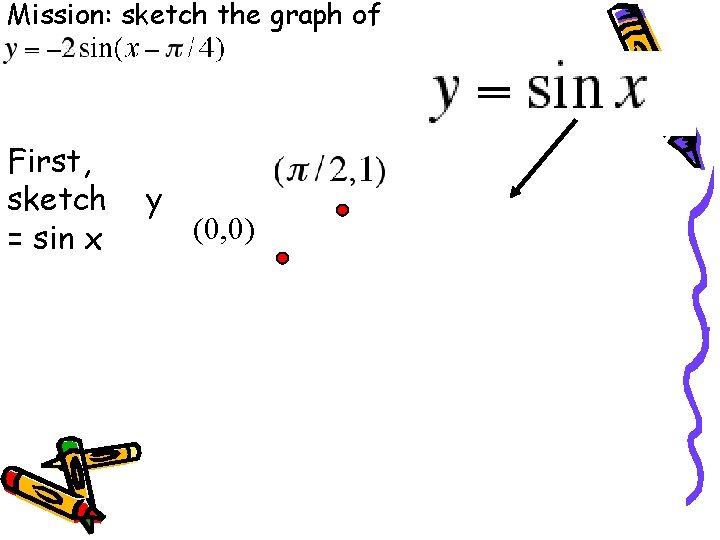
Mission: sketch the graph of First, sketch = sin x y (0, 0)
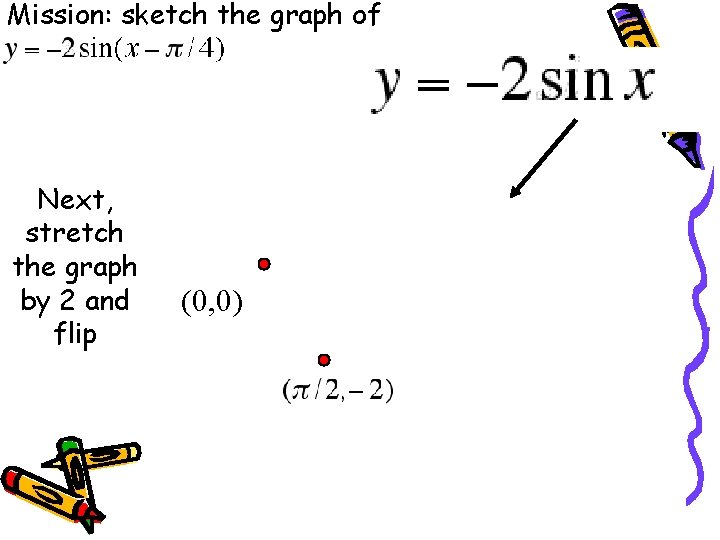
Mission: sketch the graph of Next, stretch the graph by 2 and flip (0, 0)
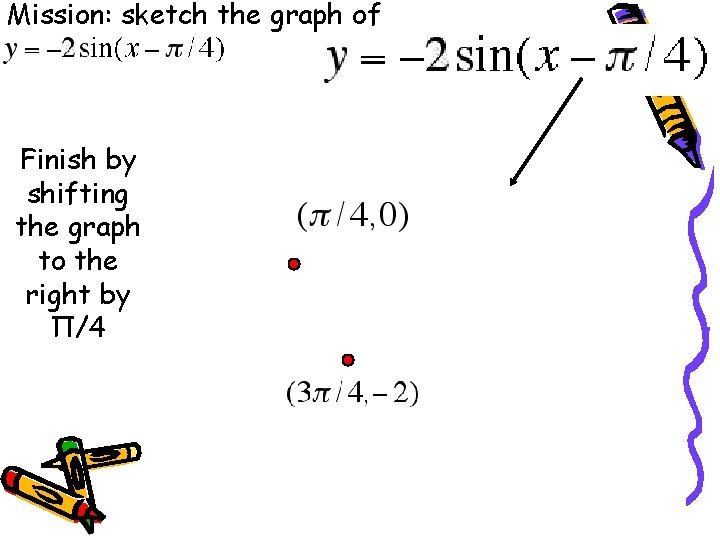
Mission: sketch the graph of Finish by shifting the graph to the right by Π/4

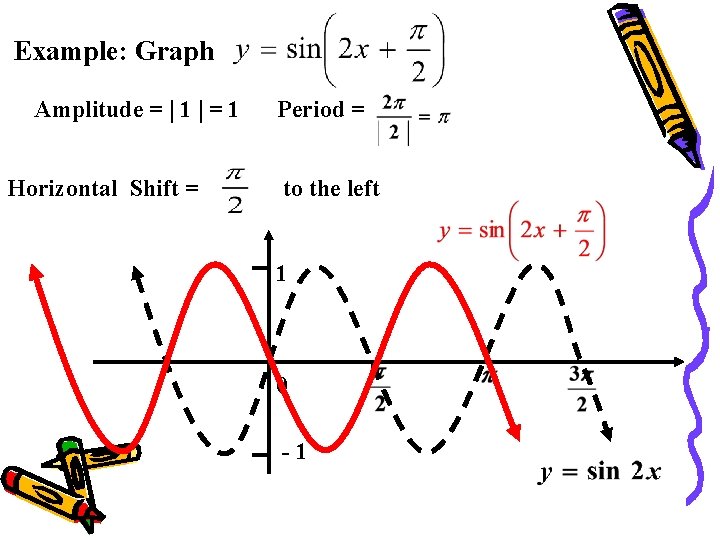
Example: Graph Amplitude = 1 = 1 Horizontal Shift = Period = to the left 1 0 -1

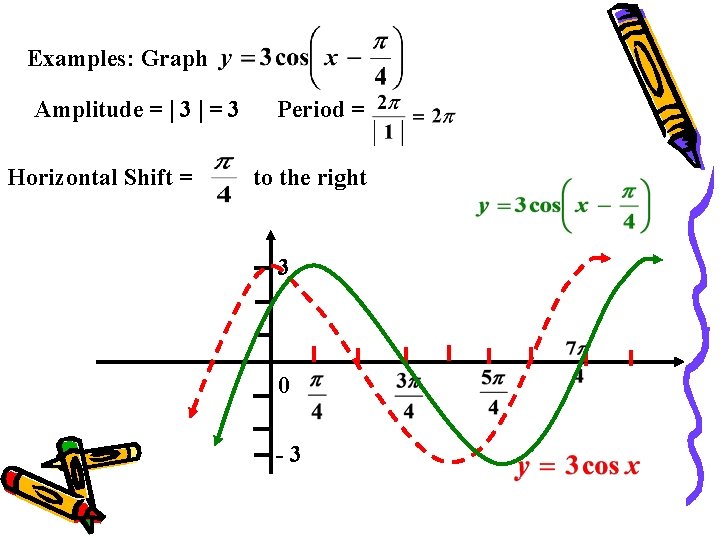
Examples: Graph Amplitude = 3 = 3 Horizontal Shift = Period = to the right 3 0 -3

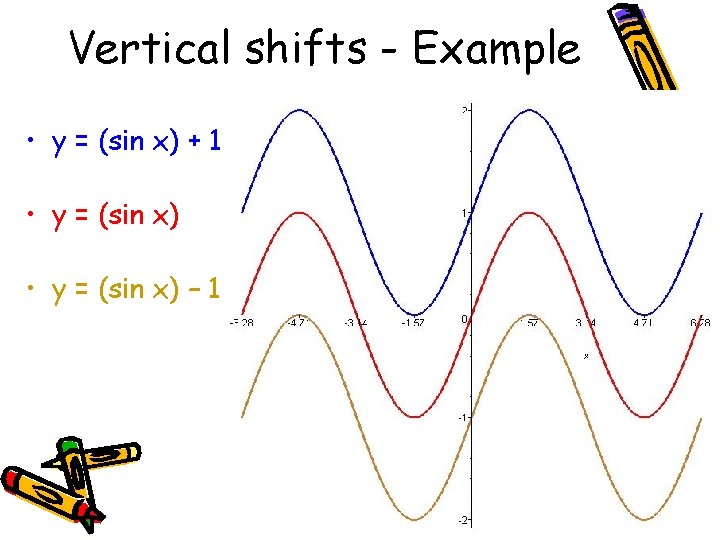
Now for our final transformation: Vertical shifts • If y = f(x) is changed to y = f(x) + d, then the graph is shifted up by d units. • If y = f(x) is changed to y = f(x) - d, then the graph is shifted down by d units.

Vertical shifts - Example • y = (sin x) + 1 • y = (sin x) – 1

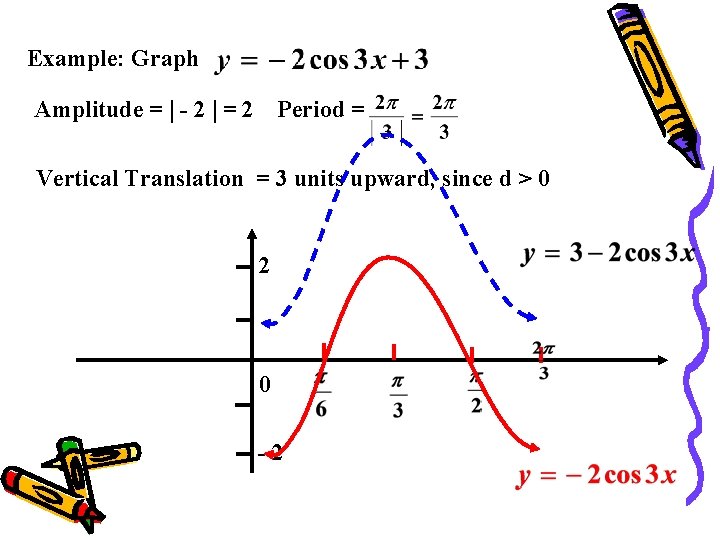
Example: Graph Amplitude = - 2 = 2 Period = Vertical Translation = 3 units upward, since d > 0 2 0 -2

Classwork: • 1. 5 Practice Worksheet- Graphs of Sine and Cosine Functions

Classwork/Homework: • Pg 167 • 15, 16, 21, 22, 25, 26, 33, 35 - 42, 56