1 5 Analyzing Graphs of Functions 2 4


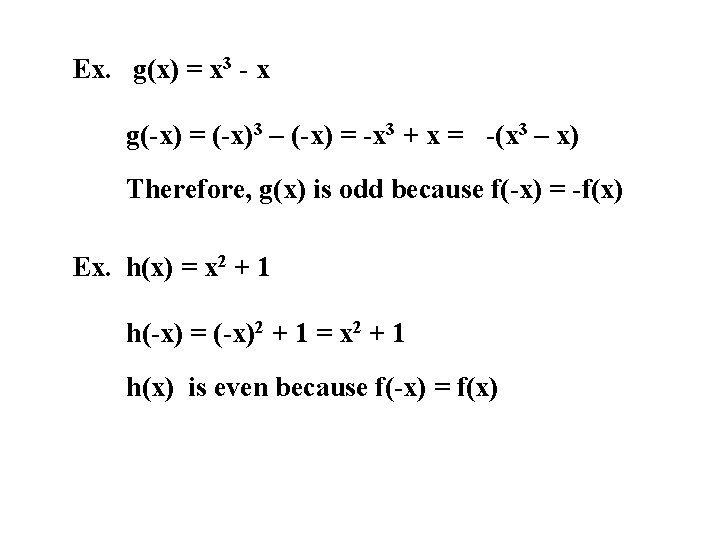
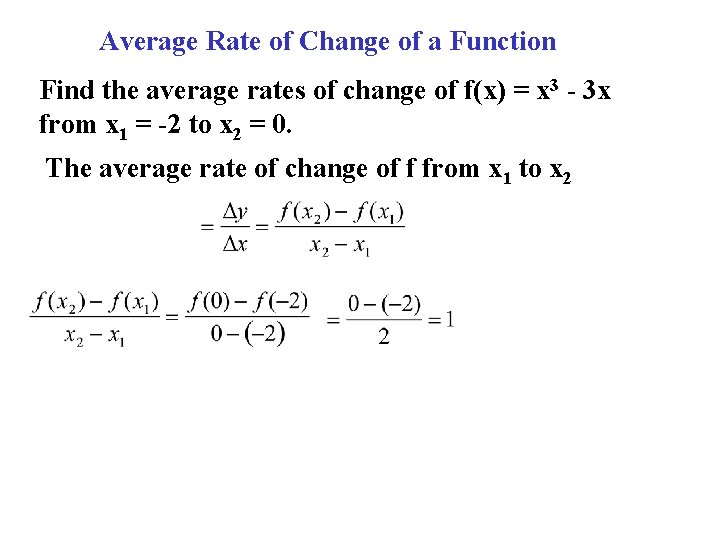

- Slides: 10

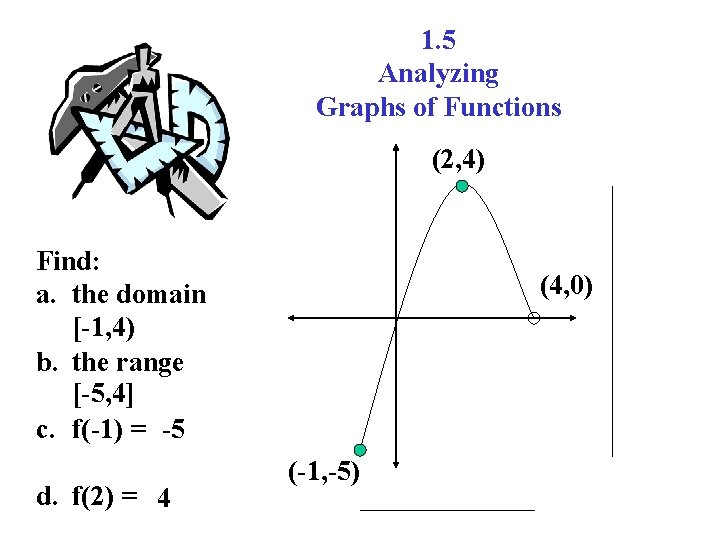
1. 5 Analyzing Graphs of Functions (2, 4) Find: a. the domain [-1, 4) b. the range [-5, 4] c. f(-1) = -5 d. f(2) = 4 (4, 0) (-1, -5)

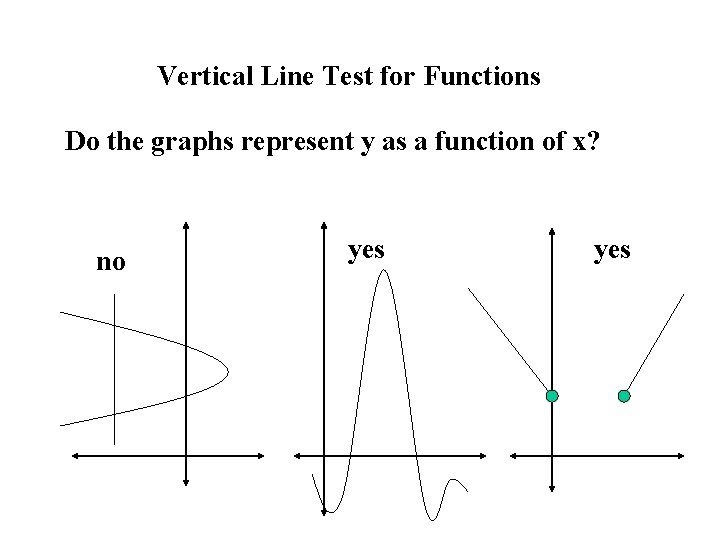
Vertical Line Test for Functions Do the graphs represent y as a function of x? no yes

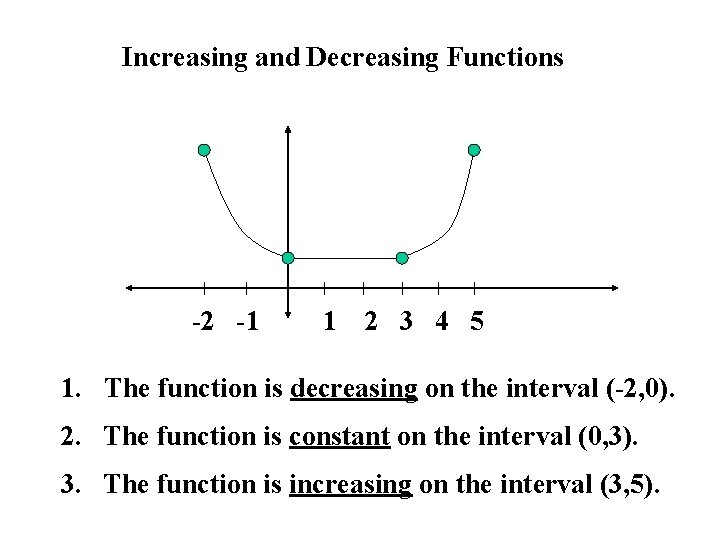
Increasing and Decreasing Functions -2 -1 1 2 3 4 5 1. The function is decreasing on the interval (-2, 0). 2. The function is constant on the interval (0, 3). 3. The function is increasing on the interval (3, 5).

A function f is increasing on an interval if, for any x 1 and x 2 in the interval, x 1 < x 2 implies f(x 1) < f(x 2) A function f is decreasing on an interval if, for any x 1 and x 2 in the interval, x 1 < x 2 implies f(x 1) > f(x 2) A function f is constant on an interval if, for any x 1 and x 2 in the interval, f(x 1) = f(x 2) go to page 57

Tests for Even and Odd Functions A function is y = f(x) is even if, for each x in the domain of f, f(-x) = f(x) An even function is symmetric about the y-axis. A function is y = f(x) is odd if, for each x in the domain of f, f(-x) = -f(x) An odd function is symmetric about the origin.
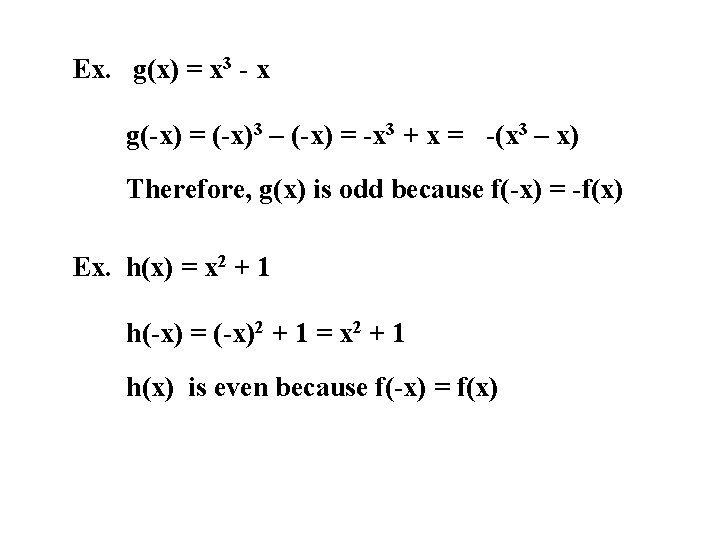
Ex. g(x) = x 3 - x g(-x) = (-x)3 – (-x) = -x 3 + x = -(x 3 – x) Therefore, g(x) is odd because f(-x) = -f(x) Ex. h(x) = x 2 + 1 h(-x) = (-x)2 + 1 = x 2 + 1 h(x) is even because f(-x) = f(x)

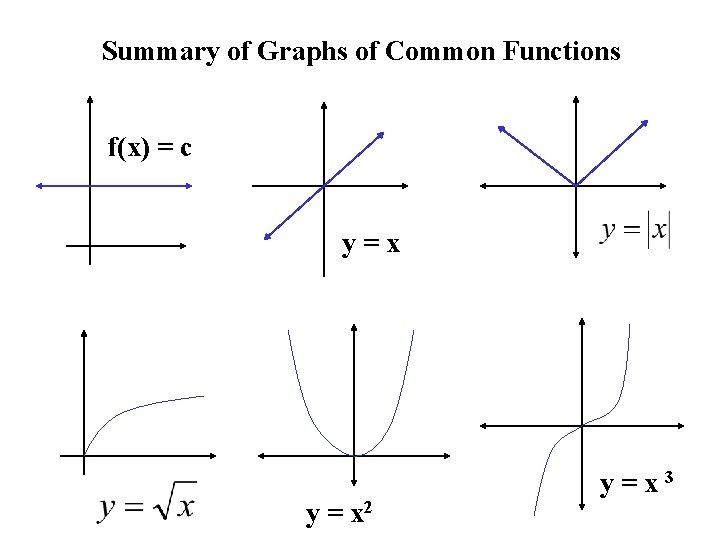
Summary of Graphs of Common Functions f(x) = c y=x y = x 2 y=x 3

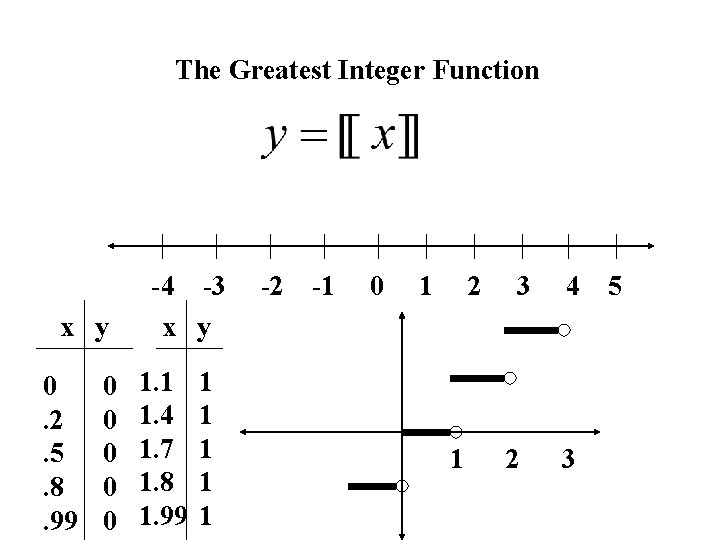
The Greatest Integer Function x y 0. 2. 5. 8. 99 0 0 0 -4 -3 x y 1. 1 1. 4 1. 7 1. 8 1. 99 1 1 1 -2 -1 0 1 2 1 3 2 4 3 5
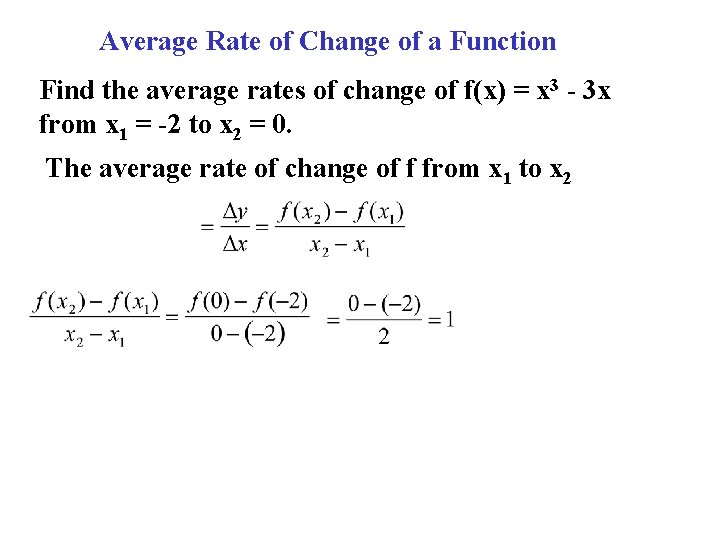
Average Rate of Change of a Function Find the average rates of change of f(x) = x 3 - 3 x from x 1 = -2 to x 2 = 0. The average rate of change of f from x 1 to x 2

Finding Average Speed The average speed of s(t) from t 1 to t 2 is Ex. The distance (in feet) a moving car is from a stoplight is given by the function s(t) = 20 t 3/2, where t is the time (in seconds). Find the average speed of the car from t 1 = 0 to t 2 = 4 seconds. What’s the average speed of the car from 4 to 9 seconds?