1 4 The Matrix Equation Ax b DEFINITION

1. 4 The Matrix Equation Ax = b • DEFINITION The product of A and x, is the linear combination of the columns of A using the corresponding entries in x as weights; that is,

EXAMPLE 1

EXAMPLE 2 v 1, v 2, v 3 Rm , EXAMPLE 3 a matrix equation

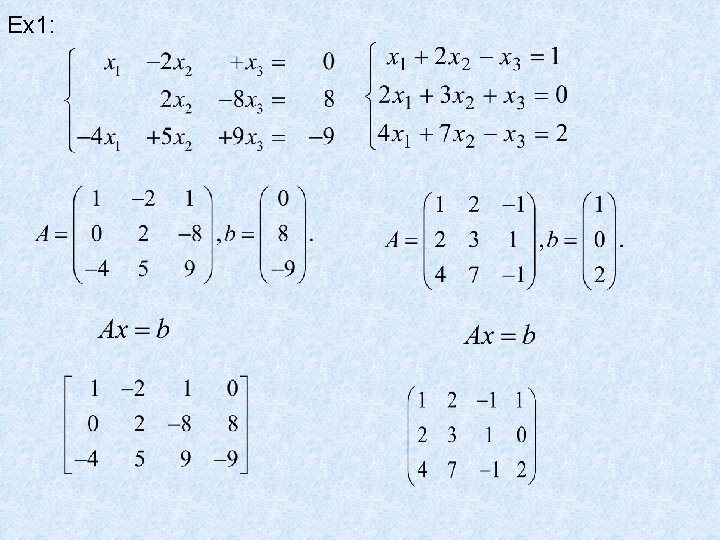
Ex 1:

THEOREM 3 The matrix equation Ax=b has the same solution set as the vector equation x 1 a 1+ x 2 a 2+ … + xnan = b, which, in turn, has the same solution set as the system of linear equations whose augmented matrix is [a 1 a 2 … an b].

Existence of Solution The equation Ax = b has a solution if and only if b is a linear combination of the columns of A.

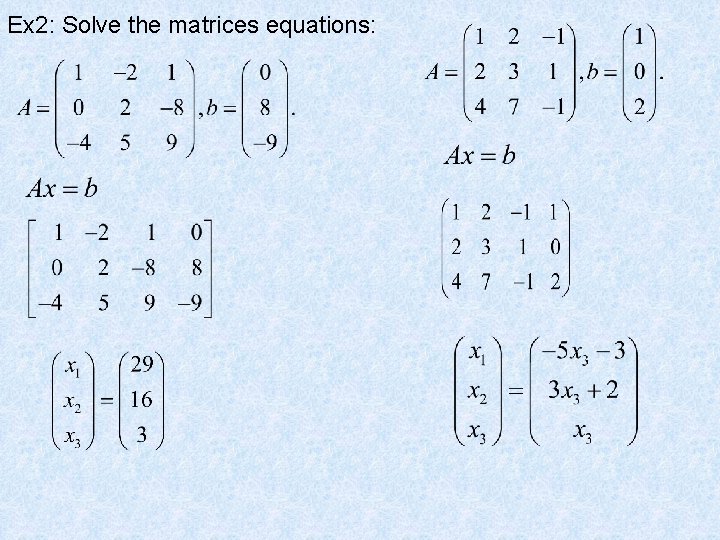
Ex 2: Solve the matrices equations:

THEOREM 4 The following statements are logically equivalent. a. For each b in Rm, the equation Ax = b has a solution. b. Each b in Rm is a linear combination of the column of A. c. The columns of A span Rm. d. A has a pivot position in every row.

EXAMPLE 4 is the equation Ax=b consistent for all possible b 1, b 2, b 3 ? No. For there are two pivot positions.

Ex 3: is the equation Ax=b consistent for all possible b 1, b 2, b 3 ? Yes. For A has a pivot position in every row

Ex 4: . is the equation Ax=b consistent for all possible b 1, b 2, b 3 ? No. For there are two pivot positions.

Computation of Ax (Row-Vector Rule for Computing Ax) The ith entry in Ax is the sum of the products of corresponding entries from row i of A and from the vector x.

EXAMPLE 5

Identity matrix I 单位矩阵 Ix=x

Properties of the Matrix-Vector Product Ax THEROM 5 If A is an m×n matrix, u and v are vectors in Rn, then a. A( u + v ) = Au+Av; b. A(cu)=c(Au).