1 4 Solving Linear Equations Linear Equations Definition
















- Slides: 18

§ 1. 4 Solving Linear Equations

Linear Equations Definition of a Linear Equation A linear equation in one variable x is an equation that can be written in the form ax + b = 0, where a and b are real numbers and a is not equal to 0. An example of a linear equation in x is 4 x + 2 = 6. Linear equations in x are first degree equations in the variable x. Blitzer, Algebra for College Students, 6 e – Slide #2 Section 1. 4

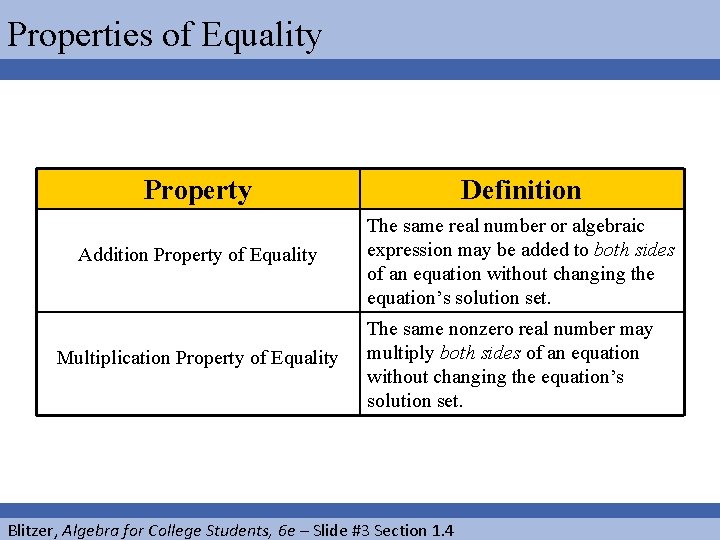
Properties of Equality Property Definition Addition Property of Equality The same real number or algebraic expression may be added to both sides of an equation without changing the equation’s solution set. Multiplication Property of Equality The same nonzero real number may multiply both sides of an equation without changing the equation’s solution set. Blitzer, Algebra for College Students, 6 e – Slide #3 Section 1. 4

Solving Linear Equations Solving a Linear Equation 1) Simplify the algebraic expressions on each side. 2) Collect all the variable terms on one side and all the numbers, or constant terms, on the other side 3) Isolate the variable and solve. 4) Check the proposed solution in the original equation. Blitzer, Algebra for College Students, 6 e – Slide #4 Section 1. 4

Solving Linear Equations EXAMPLE Solve and check: 5 - 3 x + 4 x = 1 - 7 x + 12. SOLUTION 1) Simplify the algebraic expressions on each side. 5 - 3 x + 4 x = 1 - 7 x + 12 5 + x = 13 - 7 x Combine like terms: -3 x + 4 x = x 1 + 12 = 13 Blitzer, Algebra for College Students, 6 e – Slide #5 Section 1. 4

Solving Linear Equations CONTINUED 2) Collect variable terms on one side and constant terms on the other side. 5 + x + 7 x = 13 - 7 x + 7 x 5 + 8 x = 13 5 – 5 + 8 x = 13 - 5 8 x = 8 Add 7 x to both sides Simplify Subtract 5 from both sides Simplify Blitzer, Algebra for College Students, 6 e – Slide #6 Section 1. 4

Solving Linear Equations CONTINUED 3) Isolate the variable and solve. 8 x 8 8 8 x=1 Divide both sides by 8 Simplify Blitzer, Algebra for College Students, 6 e – Slide #7 Section 1. 4

Solving Linear Equations CONTINUED 4) Check the proposed solution in the original equation. 5 - 3 x + 4 x = 2 - 7 x + 6 5 – 3(1) + 4(1) ? = 1 – 7(1) + 12 5 – 3 + 4 ? = 1 – 7 + 12 2 + 4 ? = – 6 + 12 6=6 Original equation Replace x with 1 Multiply Add or subtract from left to right Add Blitzer, Algebra for College Students, 6 e – Slide #8 Section 1. 4

Solving Linear Equations EXAMPLE Solve and check: SOLUTION 1) Simplify the algebraic expressions on each side. Multiply both sides by the LCD: 30 Distributive Property Blitzer, Algebra for College Students, 6 e – Slide #9 Section 1. 4

Solving Linear Equations CONTINUED Cancel Multiply Distribute Blitzer, Algebra for College Students, 6 e – Slide #10 Section 1. 4

Solving Linear Equations CONTINUED 14 x + 2 = 15 x Combine like terms 2) Collect variable terms on one side and constant terms on the other side. 14 x – 14 x + 2 = 15 x – 14 x 2=x Subtract 14 x from both sides Simplify 3) Isolate the variable and solve. Already done. Blitzer, Algebra for College Students, 6 e – Slide #11 Section 1. 4

Solving Linear Equations CONTINUED 4) Check the proposed solution in the original equation. ? Original Equation ? Replace x with 2 ? Simplify Blitzer, Algebra for College Students, 6 e – Slide #12 Section 1. 4

Solving Linear Equations CONTINUED 1 -0=1 Simplify 1=1 Simplify Since the proposed x value of 2 made a true sentence of 1 = 1 when substituted into the original equation, then 2 is indeed a solution of the original equation. Blitzer, Algebra for College Students, 6 e – Slide #13 Section 1. 4

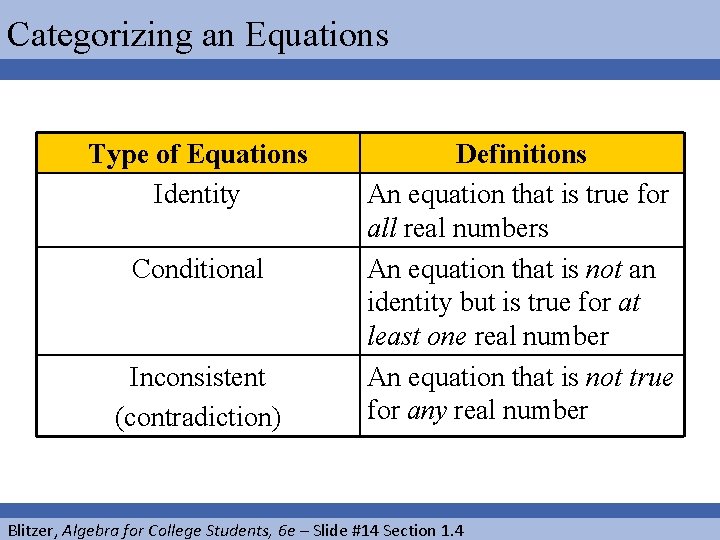
Categorizing an Equations Type of Equations Identity Conditional Inconsistent (contradiction) Definitions An equation that is true for all real numbers An equation that is not an identity but is true for at least one real number An equation that is not true for any real number Blitzer, Algebra for College Students, 6 e – Slide #14 Section 1. 4

Categorizing an Equation EXAMPLE Solve and determine whether the equation is an identity, a conditional equation or an inconsistent equation. 5 + 4 x = 9 x + 5 SOLUTION 5 + 4 x = 9 x + 5 5 - 5 + 4 x = 9 x + 5 - 5 4 x = 9 x 4 x – 4 x = 9 x – 4 x Subtract 5 from both sides Simplify Subtract 4 x from both sides Blitzer, Algebra for College Students, 6 e – Slide #15 Section 1. 4

Categorizing an Equation CONTINUED 0 = 5 x Simplify Divide both sides by 5 0=x Simplify The original equation is only true when x = 0. Therefore, it is a conditional equation. Blitzer, Algebra for College Students, 6 e – Slide #16 Section 1. 4

Categorizing an Equation EXAMPLE Solve and determine whether the equation is an identity, a conditional equation or an inconsistent equation. 5 – (2 x – 4) = 4(x +1) - 2 x SOLUTION 5 – (2 x – 4) = 4(x +1) - 2 x 5 – 2 x +4 = 4 x + 4 -2 x 9 - 2 x = 4 - 2 x 9=4 Distribute the -1 and the 4 Simplify Add 2 x to both sides. Since after simplification we see a contradiction, we know that the original equation is inconsistent and can never be true for any x. Blitzer, Algebra for College Students, 6 e – Slide #17 Section 1. 4

Categorizing an Equation EXAMPLE Solve and determine whether the equation is an identity, a conditional equation or an inconsistent equation. 3 + 2 x = 3(x +1) - x SOLUTION 3 + 2 x = 3(x +1) - x 3 + 2 x = 3 x + 3 - x Distribute the 3 3 + 2 x = 2 x + 3 Simplify Since after simplification we can see that the left hand side (LHS) is equal to the RHS of the equation, this is an identity and is always true for all x. Blitzer, Algebra for College Students, 6 e – Slide #18 Section 1. 4