1 4 Solving Equations Using a Graphing Utility


















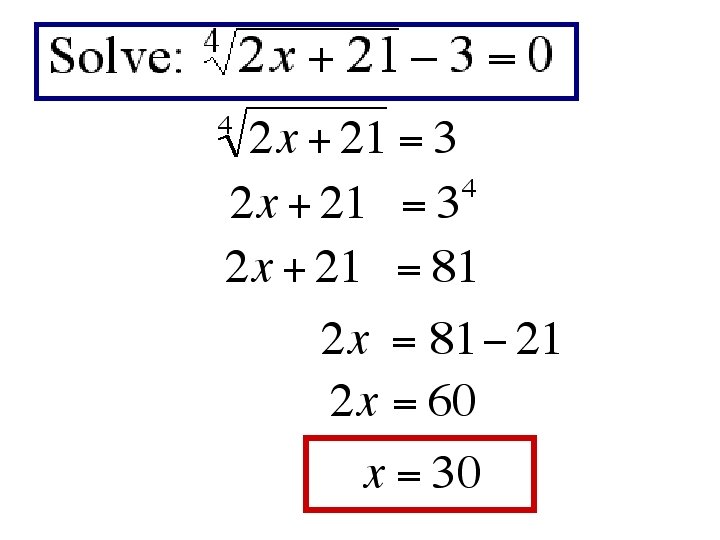
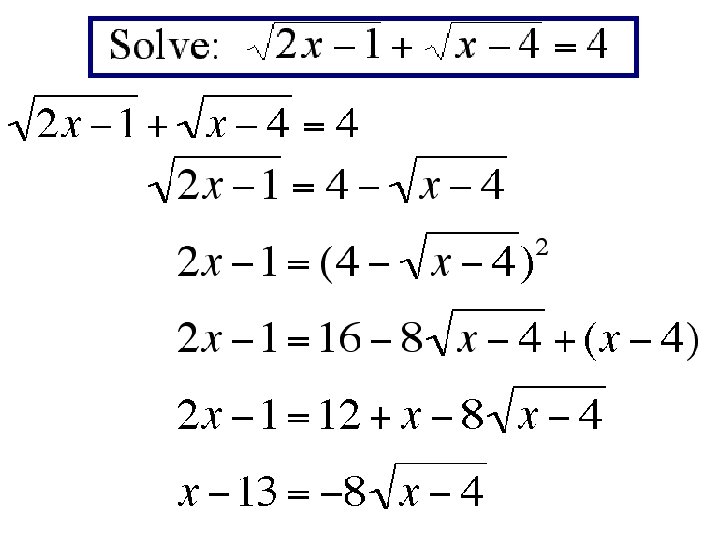
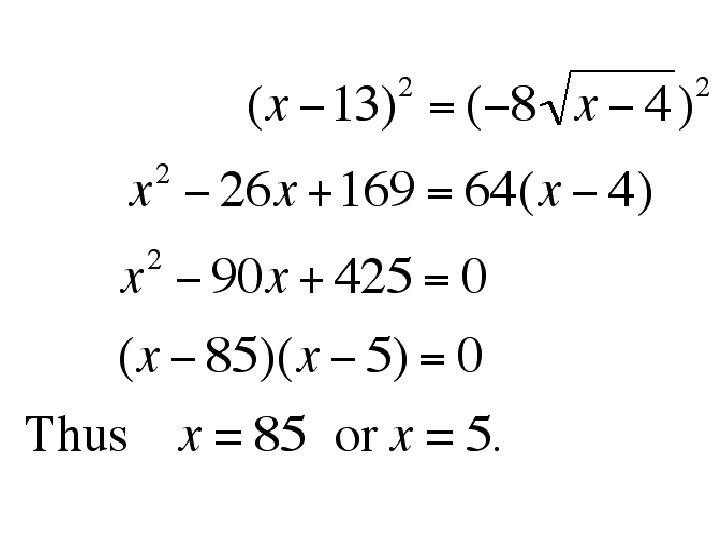



- Slides: 24

1. 4 Solving Equations Using a Graphing Utility

An equation in one variable is a statement in which two expressions, at least one containing the variable, are equal. To solve an equation means to find all those values of the variable that result in a true statement.

Procedures that Result in Equivalent Equations • Interchange the two sides of the equation. • Simplify each side. (Combine like terms, eliminate parentheses. . . ) • Add or subtract the same expression on both sides. • Multiply both sides of the equation by the same nonzero expression. • If one side is zero and the other can be factored use the Zero. Product Property.

Steps for Solving Equations Algebraically • List any restrictions on the domain of the variable. • Simplify the equation by replacing the original by a succession of equivalent equations using the procedures listed earlier. • If the result is a product of factors equal to 0, use the Zero-Product Property. • Check your solution(s).

Solve a linear equation 5 x - 4 = 7.

Solve by Zero-Product Property

Zero-Product Property The solution set is {0, 6}.

Steps for Approximating Solutions of Equations Using Zero (or Root) • Write the equation in the form {expression in x } = 0 • Graph Y 1= {expression in x }. • Use ZERO (or ROOT) to determine each x -intercept of the graph.

Steps for Approximating Solutions of Equations Using Intersect • Graph Y 1={expression in x on the left hand side of equation}. • Graph Y 2={expression in x on the right hand side of equation}. • Use INTERSECT to determine each xcoordinate of the points of intersection.

Linear Equations

Quadratic Equations

Methods for Solving Quadratic Equations • • • Factoring Graphing Square Root Method Complete the Square Method Quadratic Formula

The Square Root Method

Solve the following quadratic equation: Using the Square Root Method

Quadratic Formula


Discriminant of a Quadratic Equation is called a discriminant >0, there are 2 unequal real solutions. =0, there is a repeated real solution. <0, there is no real solution.

Equations Containing Radicals
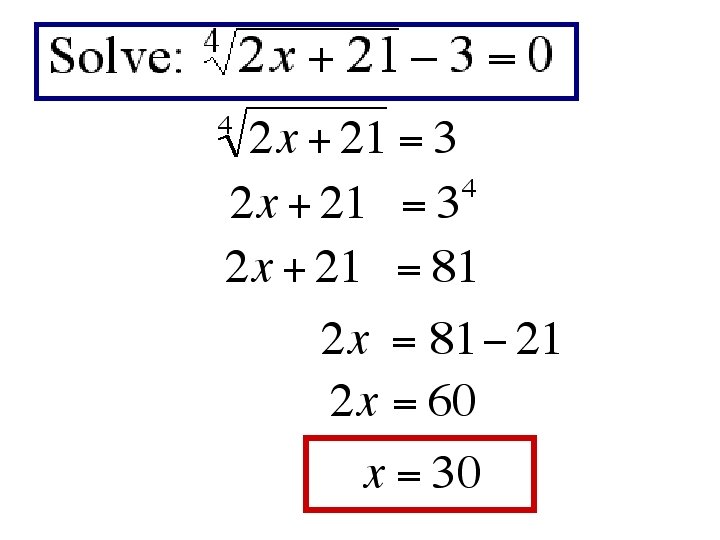
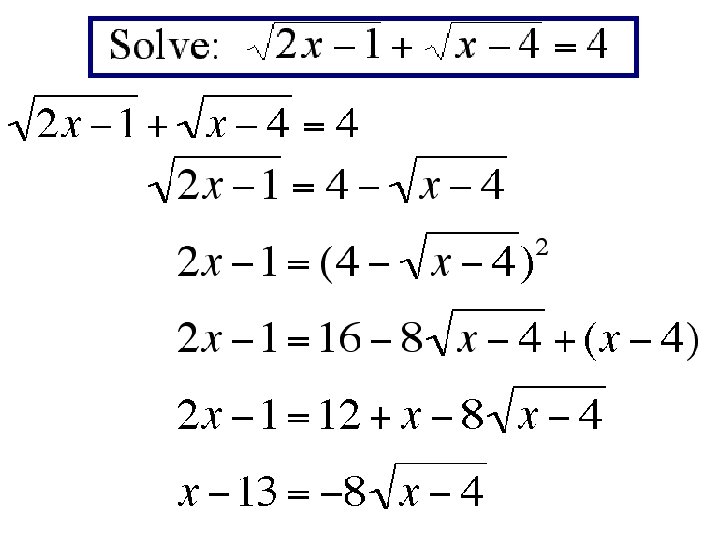
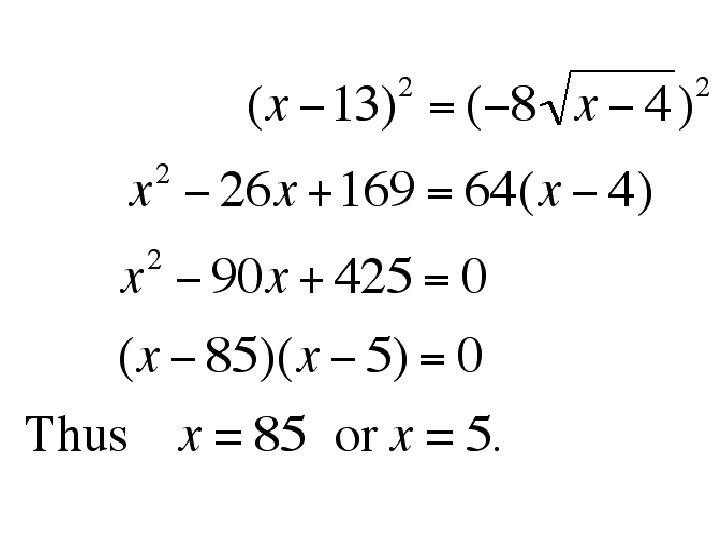

Thus 85 is NOT a solution. The solution set is {5}.

Equations Involving Absolute Value

The solution set is {7, -6}.