1 4 MOMENTUM IN TWO DIMENSIONS Momentum momentum

1. 4 MOMENTUM IN TWO DIMENSIONS

Momentum • momentum of an object to be the product of mass (m) and velocity (v). • Momentum is a vector quantity with SI Units of kgms-1 (or Ns, since 1 N = 1 kgms-2).

Momentum in 2 -Dimensions • Vector Form of Newton’s Second Law of Motion • Consider a particle reflecting off a surface without a change in speed. • A particle has m = 2 kg and initial velocity vi = 20 m s-1 and the collision lasts for t = 0. 2 s, then determine the average force acting on the particle. vf = -20 ms-1 Acceleration a is given by, m vi vf

Momentum in 2 -Dimensions • Vector Form of Newton’s Second Law of Motion • a = -200 ms-1 • Acceleration is in opposite direction to vi. • and since F = m a • then F = 2 x (-200) • = -400 N • ie. 400 N away from the wall • Ie, the wall applied a force of 400 N on the ball away from the wall and due to Newtons 3 rd Law, the ball exerted a force of 400 N towards the wall.

Vector Form of Newton’s Second Law

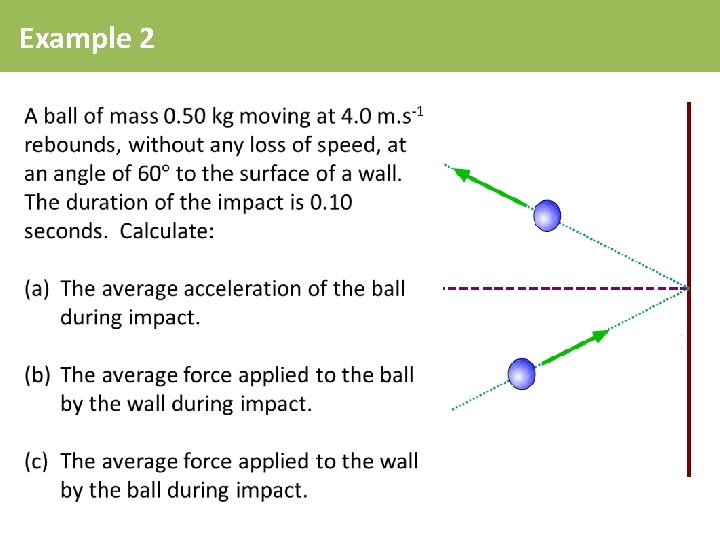
Example 1 A ball of mass 0. 50 kg moving at 4. 0 m. s-1 rebounds off a wall, without any loss of speed, along the normal to the wall. The duration of the impact is 0. 080 seconds. Calculate: vi = 4. 0 m. s-1 vf = - 4. 0 m. s-1 Calculate: (a) The average acceleration of the ball during impact. (b) The average force applied to the ball by the wall during impact. (c) The average force applied to the wall by the ball during impact.

Example 2

Newton’s Second Law in Terms of Momentum provided that the mass of the particle is fixed.

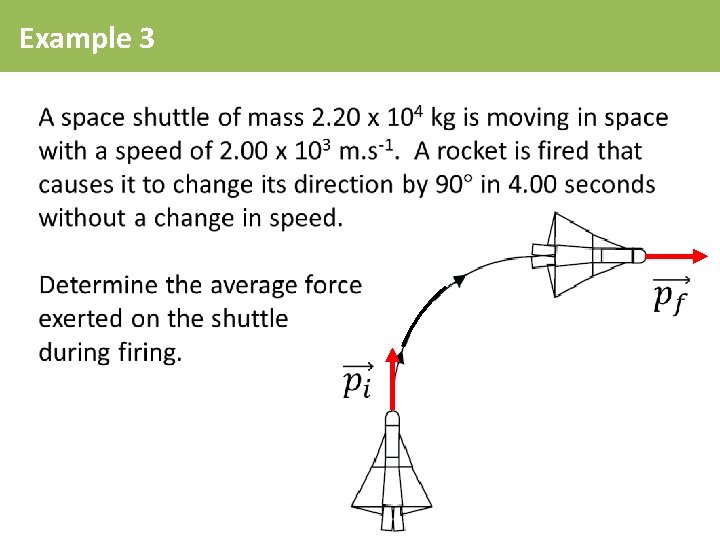
Example 3

Example 4 A ball of mass 0. 07 kg moving at 1. 0 m. s-1 rebounds off a wall with a velocity of 0. 60 m. s-1 as shown in the diagram. The duration of the impact is 0. 010 seconds. vi = 1. 0 m. s-1 vf = - 0. 60 m. s-1 Calculate: (a) The average force acting on the ball during impact. (b) The average acceleration of the ball during impact. (c) The average force exerted on the wall during impact.

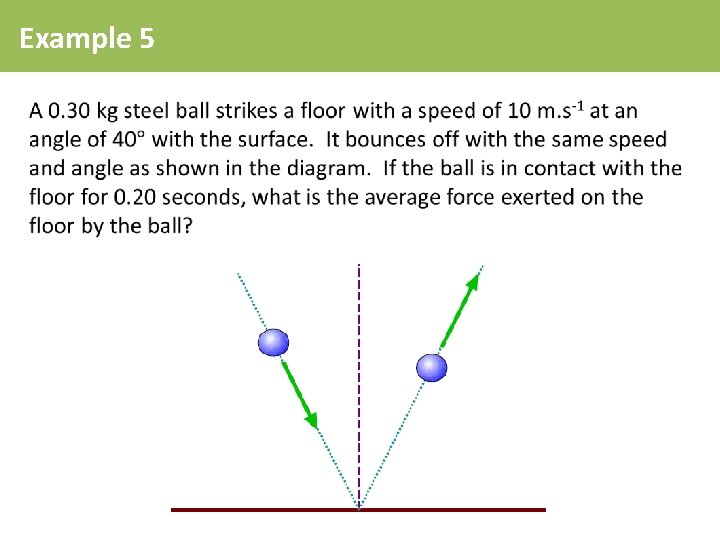
Example 5

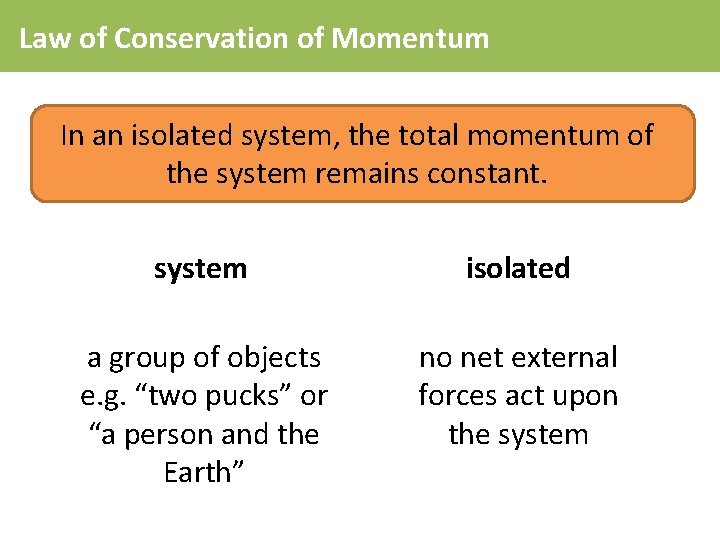
Law of Conservation of Momentum In an isolated system, the total momentum of the system remains constant. system isolated a group of objects e. g. “two pucks” or “a person and the Earth” no net external forces act upon the system

Law of Conservation of Momentum

Multi-Image Photographs The collision of two objects (or the explosion of one) can be documented by taking a multi-image photograph. Using this, it is possible to determine whether momentum is conserved. See Power. Point (Multi image collision examples)

Conservation of Momentum Calculations 1. Draw diagrams showing the situation before and after impact. 2. Label the momenta of each object in these diagrams using subscripts. 3. Find equations for the total momentum before and the total momentum after impact. BE CAREFUL TO USE VECTORS. 4. Use the Law of Conservation of Momentum and solve for the unknown.

Conservation of Momentum • NB. (1) No net external forces means an isolated system. • (2) Total linear momentum refers to both size and direction (vector addition is needed to find the total) • (3) Conserved means that it stays the same (throughout the interaction) • (4) The objects may be deformed, broken apart, stuck together or exploded. However momentum is still conserved as long as no net external forces act.

Momentum in 2 -Dimensions • The Law of Conservation of Momentum Example A rail wagon of mass 4. 0 tones, moving 3 ms-1 North collides with another wagon of mass 2. 0 tones. They stick together. What is their combined velocity? Take North to be the positive direction,

Momentum in 2 -Dimensions • The Law of Conservation of Momentum Assuming the system isolated, linear momentum is conserved.

Momentum in 2 -Dimensions • The Law of Conservation of Momentum Example A body at rest explodes breaking into 3 pieces. One piece flies off due East at 30 ms-1. Another piece flies of due North at 30 ms-1. What is the velocity of the 3 rd piece if its mass is 3 times that of the other pieces?

Example 6 Cart A is travelling North with a velocity of 5. 4 m. s-1 while Cart B is travelling South at 8. 3 m. s-1. The mass of Cart A is 13 kg and the mass of Cart B is 9. 0 kg. The carts collide and Cart B rebounds with a velocity of 7 m. s-1. Determine the velocity of Cart A after the collision.

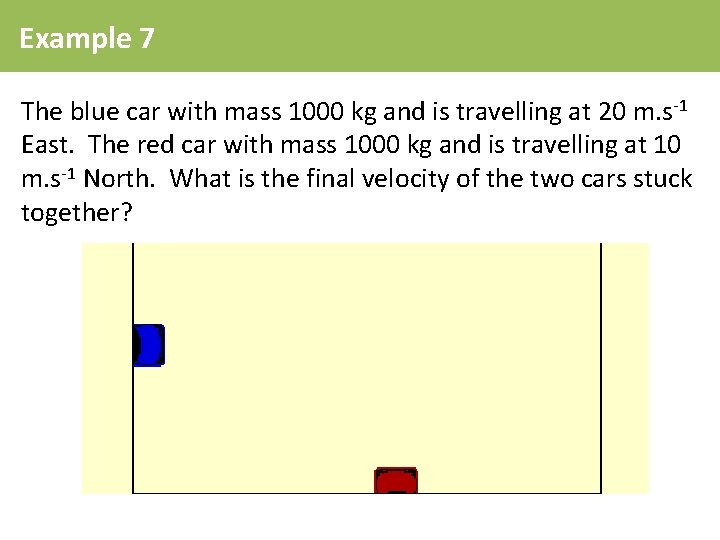
Example 7 The blue car with mass 1000 kg and is travelling at 20 m. s-1 East. The red car with mass 1000 kg and is travelling at 10 m. s-1 North. What is the final velocity of the two cars stuck together?

Example 8 A spherical mass of 9. 0 kg explodes into 3 pieces. One piece, of mass 3. 0 kg flies off due North at 10 m. s-1 whereas another piece of mass 4. 0 kg is thrown West at a speed of 13 m. s-1. Find the velocity of the third piece.

Application: Spacecraft Propulsion Rockets Initially the rocket has no momentum. When the gases leave the back of the rocket, their momentum must be balanced by the rocket gaining momentum forwards.

Application: Spacecraft Propulsion https: //www. youtube. com/watch? v=rt 5 dcrm 8 X 1 w

Solar Sails

Solar Sails Consider a photon reflected from a solar sail The photon’s change in momentum is directed away from the sail. Hence the sail must gain momentum in the opposite direction of the photon (Conservation of Momentum).

Solar Sails sail

Solar Sails sail

Solar Sails