1 4 Measuring Angles Parts of an Angle

Parts of an Angle • Formed by the union of two rays with the

Types of Angles Acute Right Obtuse • Congruent Angles • Angles with the same

Example 1: 1). Name the angle below. Name the sides and the vertex of

Protractor Postulate • Consider and a point on one side of. Every ray of

Postulate 1 -8: Angle Addition Postulate • If point B is in the interior

Classwork: p. 31 #’s 6, 7, 12 -14, 18, 20, 22, 23, 29 -31

Types of Angle Pairs • Adjacent Angles Two coplanar angles with a: common side

Example 1: Use the diagram below. Is each statement true? Explain. and are adjacent

Assumptions About Angles • Assumptions you can make: 1. Angles are adjacent 2. Angles

Postulate 1 -9: Linear Pair Postulate A Linear Pair of angles are angles that

Theorem 2 -1: Vertical Angle Theorem Vertical angles are congruent and Example 3: What

Angle Bisector two • A ____ which divides an angle into ______ ray ________

Homework: p. 38 # 7 -23 odd, 26 -32 even

Slides: 16

Download presentation

1 -4: Measuring Angles

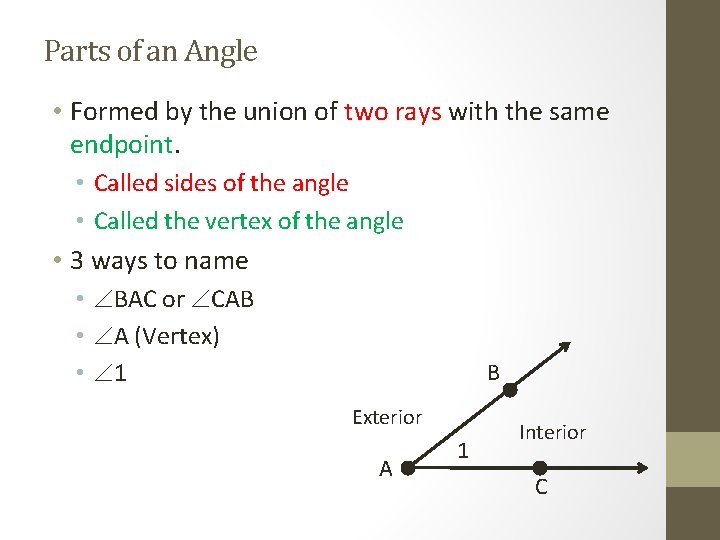
Parts of an Angle • Formed by the union of two rays with the same endpoint. • Called sides of the angle • Called the vertex of the angle • 3 ways to name • BAC or CAB • A (Vertex) • 1 B Exterior A 1 Interior C

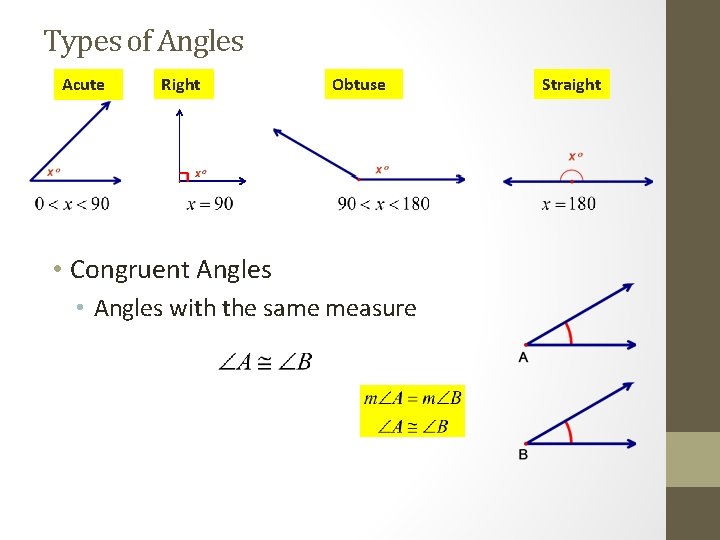
Types of Angles Acute Right Obtuse • Congruent Angles • Angles with the same measure Straight

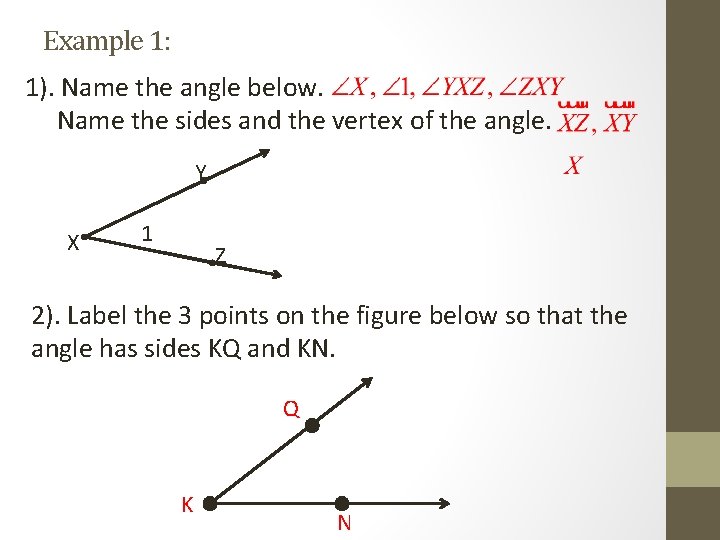
Example 1: 1). Name the angle below. Name the sides and the vertex of the angle. Y X 1 Z 2). Label the 3 points on the figure below so that the angle has sides KQ and KN. Q K N

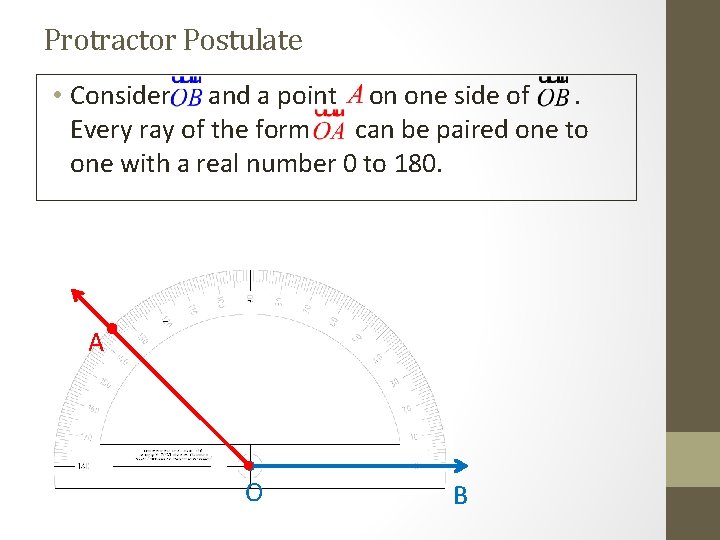
Protractor Postulate • Consider and a point on one side of. Every ray of the form can be paired one to one with a real number 0 to 180. A O B

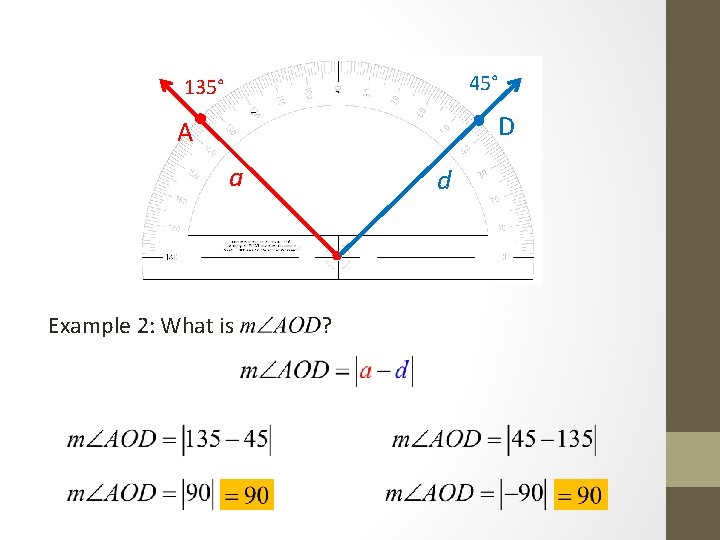
45° 135° D A a Example 2: What is d ?

Postulate 1 -8: Angle Addition Postulate • If point B is in the interior of Example 3: If , what are , then: and ?

Classwork: p. 31 #’s 6, 7, 12 -14, 18, 20, 22, 23, 29 -31

1 -5: Exploring Angle Pairs

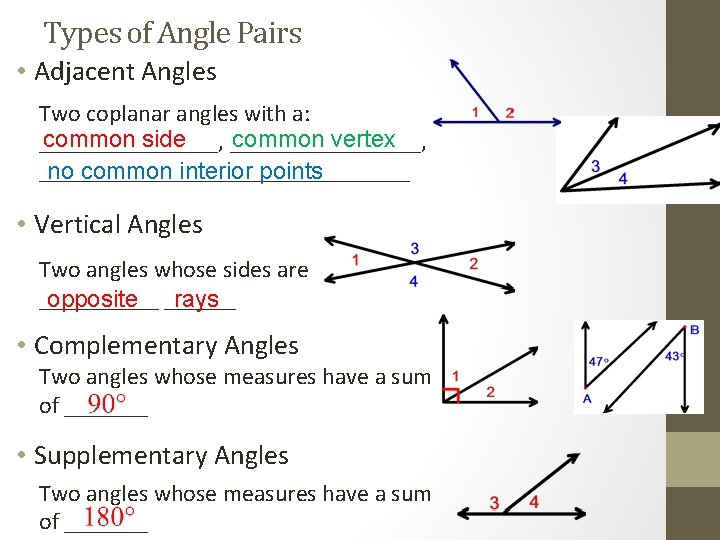
Types of Angle Pairs • Adjacent Angles Two coplanar angles with a: common side common vertex _______________, ________________ no common interior points • Vertical Angles Two angles whose sides are _____ opposite ______ rays • Complementary Angles Two angles whose measures have a sum of _______ • Supplementary Angles Two angles whose measures have a sum of _______

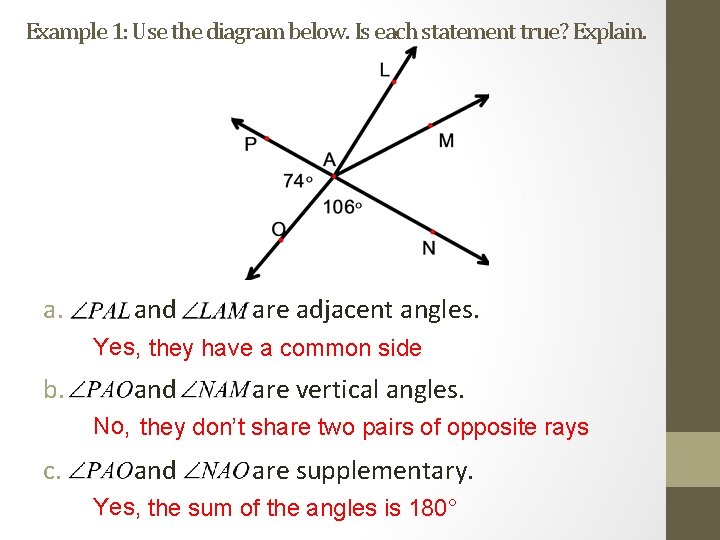
Example 1: Use the diagram below. Is each statement true? Explain. and are adjacent angles. Yes, they have a common side b. and are vertical angles. No, they don’t share two pairs of opposite rays c. and are supplementary. Yes, the sum of the angles is 180°

Assumptions About Angles • Assumptions you can make: 1. Angles are adjacent 2. Angles are adjacent and supplementary 3. Angles are vertical angles • Assumptions you can’t make: 1. Angles or segments are congruent 2. An angle is a right angle 3. Angles are complementary

Postulate 1 -9: Linear Pair Postulate A Linear Pair of angles are angles that are both supplementary and adjacent. Ex 2 What are the measures of and ?

Theorem 2 -1: Vertical Angle Theorem Vertical angles are congruent and Example 3: What is the value of x? What are the angle measures?

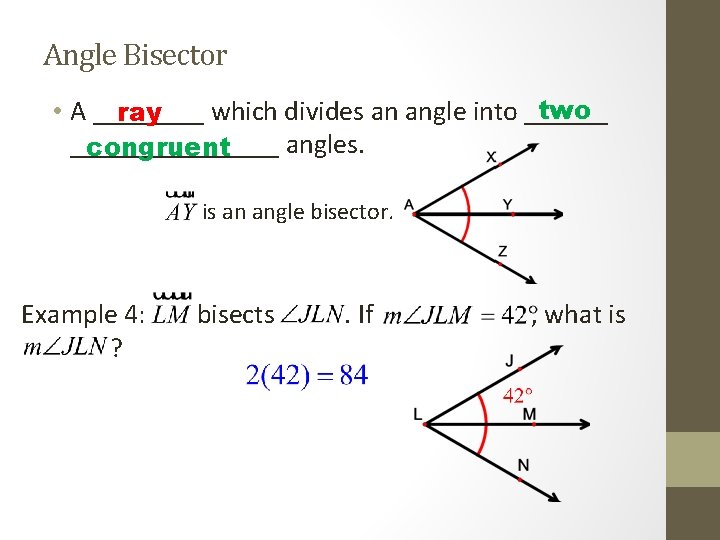
Angle Bisector two • A ____ which divides an angle into ______ ray ________ angles. congruent is an angle bisector. Example 4: ? bisects . If , what is

Homework: p. 38 # 7 -23 odd, 26 -32 even