1 4 Lines OBJECTIVES 1 FIND THE SLOPES

1. 4 Lines OBJECTIVES: 1. FIND THE SLOPES OF LINES, INCLUDING PARALLEL AND PERPENDICULAR LINES 2. GRAPH LINES 3. WRITE THE EQUATIONS OF LINES, INCLUDING HORIZONTAL AND VERTICAL LINES

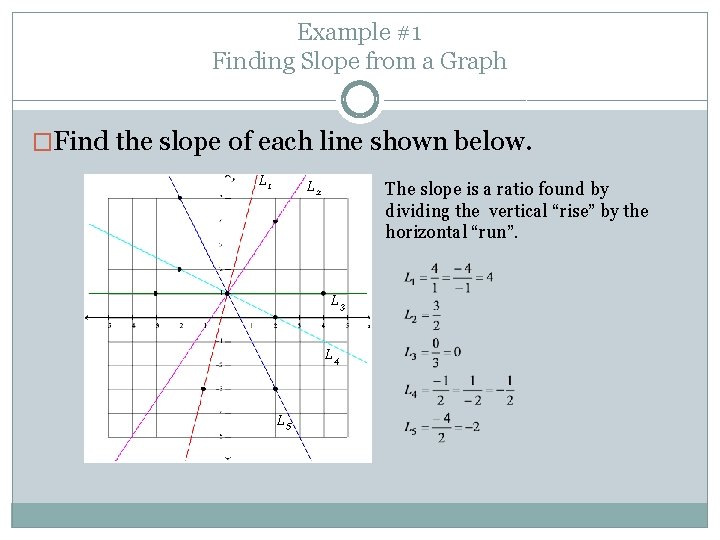
Example #1 Finding Slope from a Graph �Find the slope of each line shown below. L 1 L 2 The slope is a ratio found by dividing the vertical “rise” by the horizontal “run”. L 3 L 4 L 5

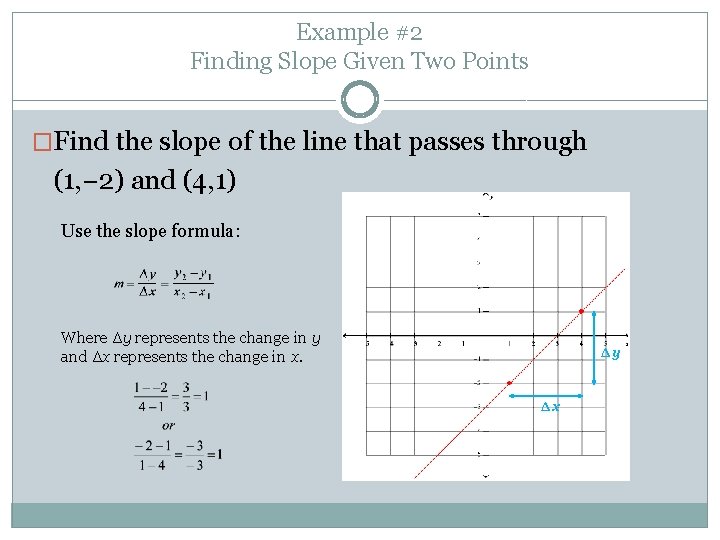
Example #2 Finding Slope Given Two Points �Find the slope of the line that passes through (1, − 2) and (4, 1) Use the slope formula: Where Δy represents the change in y and Δx represents the change in x. Δy Δx

Example #3 Solving for a Variable Given Slope �Find a number t such that the line passing through the two given points has a slope of − 3. 1. Set up a proportion. 2. Cross multiply and solve for t.

Example #4 Slope-Intercept Form � Find the slope and y-intercept of the following equation. 1) Write the equation into slope-intercept form: m is the slope and b is the y-intercept 2) The slope is then -14 and the y-intercept is 19.

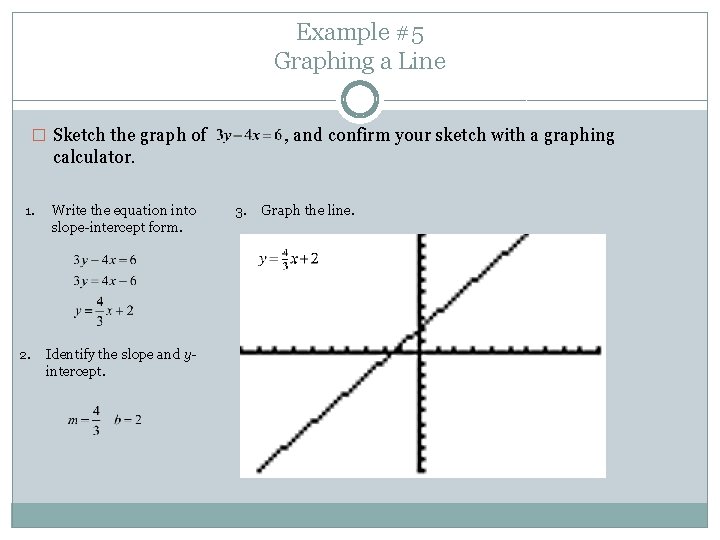
Example #5 Graphing a Line � Sketch the graph of , and confirm your sketch with a graphing calculator. 1. Write the equation into slope-intercept form. 2. Identify the slope and yintercept. 3. Graph the line.

Example #6 Writing the Equation of a Line � Sketch the graph and find the equation of the line that passes through the point (− 2, 5) with slope − 3. Write the equation in slope-intercept form. Method 1: Use the point-slope form

Example #6 Writing the Equation of a Line � Sketch the graph and find the equation of the line that passes through the point (− 2, 5) with slope − 3. Write the equation in slope-intercept form. Method 2: Use the slope-intercept form

Example #6 Writing the Equation of a Line � Sketch the graph and find the equation of the line that passes through the point (− 2, 5) with slope − 3. Write the equation in slope-intercept form. Graph:

Example #7 Linear Depreciation � An office buys a new color copier for $8000. Four years later its value is $2320. Assume that the copier depreciates linearly. 1. Write the equation that represents value as a function of years. OR

Example #7 Linear Depreciation � An office buys a new color copier for $8000. Four years later its value is $2320. Assume that the copier depreciates linearly. 2. Find its value three years after it was purchased, that is, the y-value when x = 3.

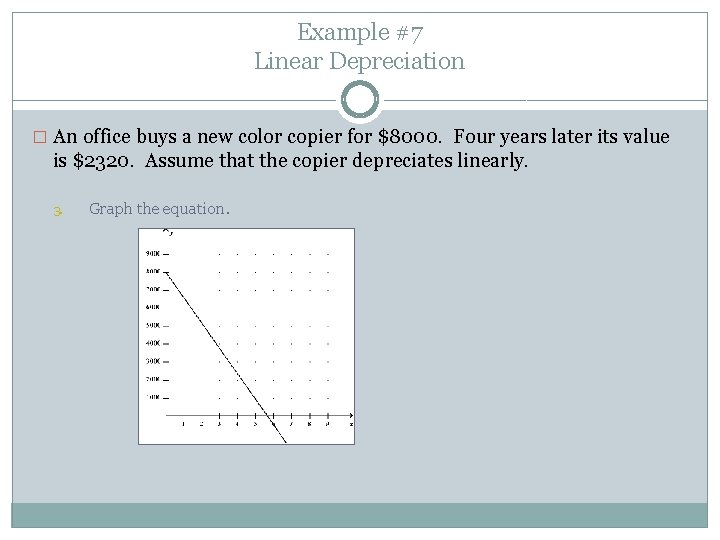
Example #7 Linear Depreciation � An office buys a new color copier for $8000. Four years later its value is $2320. Assume that the copier depreciates linearly. 3. Graph the equation.

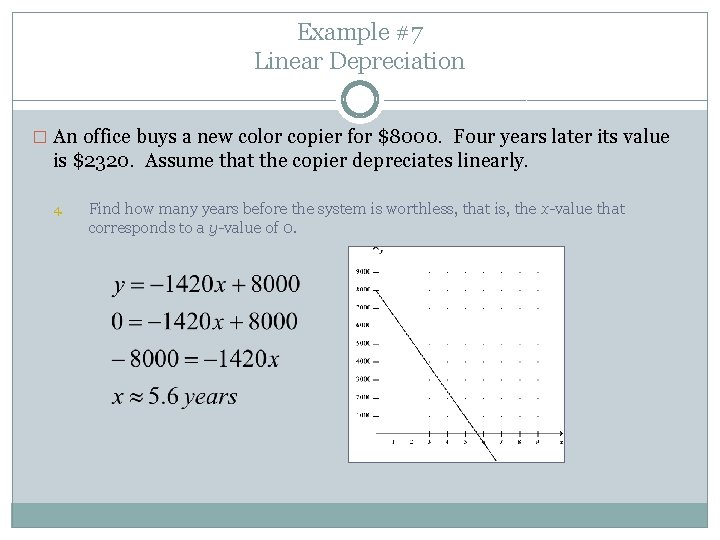
Example #7 Linear Depreciation � An office buys a new color copier for $8000. Four years later its value is $2320. Assume that the copier depreciates linearly. 4. Find how many years before the system is worthless, that is, the x-value that corresponds to a y-value of 0.

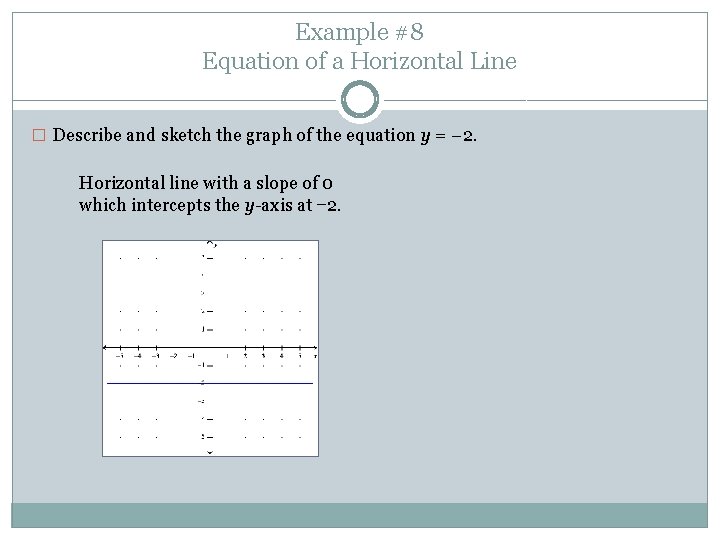
Example #8 Equation of a Horizontal Line � Describe and sketch the graph of the equation y = − 2. Horizontal line with a slope of 0 which intercepts the y-axis at − 2.

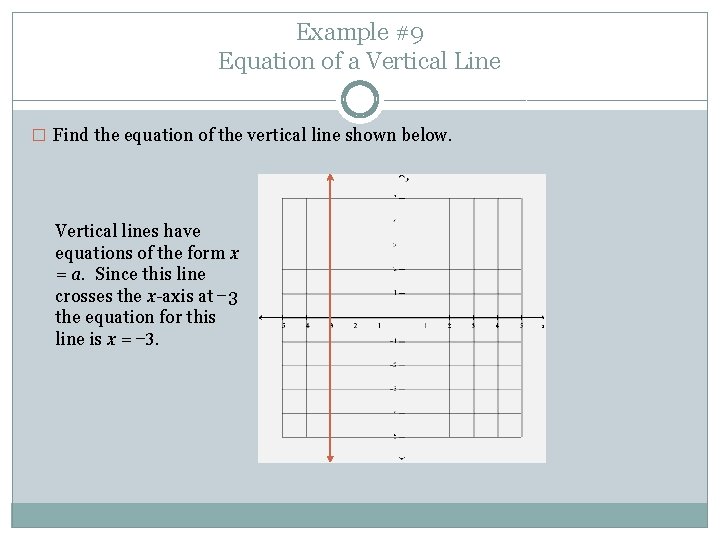
Example #9 Equation of a Vertical Line � Find the equation of the vertical line shown below. Vertical lines have equations of the form x = a. Since this line crosses the x-axis at − 3 the equation for this line is x = − 3.

Example #10 Parallel and Perpendicular Lines � Identify whether the following lines are parallel, perpendicular, or neither, with the given equation. A. Since the two lines have the same slopes they are parallel.

Example #10 Parallel and Perpendicular Lines � Identify whether the following lines are parallel, perpendicular, or neither, with the given equation. B. Since the slopes are opposite reciprocals of each other then they are perpendicular.

Example #10 Parallel and Perpendicular Lines � Identify whether the following lines are parallel, perpendicular, or neither, with the given equation. C. Since the slopes are not the same nor are they opposite reciprocals of each other, then they are neither parallel or perpendicular.

Example #11 Parallel and Perpendicular Lines � Find the equation of the lines through the point (− 4, 2) given the line M whose equation is shown below. A. Parallel to M. For parallel lines use the same slope. 1. Find the slope of line M. 2. Write the equation of the line.

Example #11 Parallel and Perpendicular Lines � Find the equation of the lines through the point (− 4, 2) given the line M whose equation is shown below. B. Perpendicular to M. For perpendicular lines use slopes that are opposite reciprocals.