1 4 FORMULAS FOR LINEAR FUNCTIONS 1 Finding

1. 4 FORMULAS FOR LINEAR FUNCTIONS 1

Finding a Formula for a Linear Function from a Table of Data Example 1 The following table gives data from a linear function for a grapefruit thrown into the air. Find the formula for the function. t, time (sec) v, velocity (ft/sec) 1 2 3 48 16 -16 Solution We will look for a function of the form y = mx + b and begin by computing the slope: Now we can determine b using m and the point (2, 16): y = -32 x+ b; 16 = -32 (2) + b which gives b = 80 So the formula for our function is 2

Exercise 26 The following table gives data from a linear function. Find a formula for the function. Temperature, x (◦F) Temperature, y = f(x) (◦C) 32 41 68 0 5 20 Solution We will look for a function of the form y = mx + b and begin by computing the slope: Now we can determine b using m and the point (32, 0): y = 5/9 x + b; 0 = 5/9 (32) + b which gives b = -160/9 So the formula for our function is 3

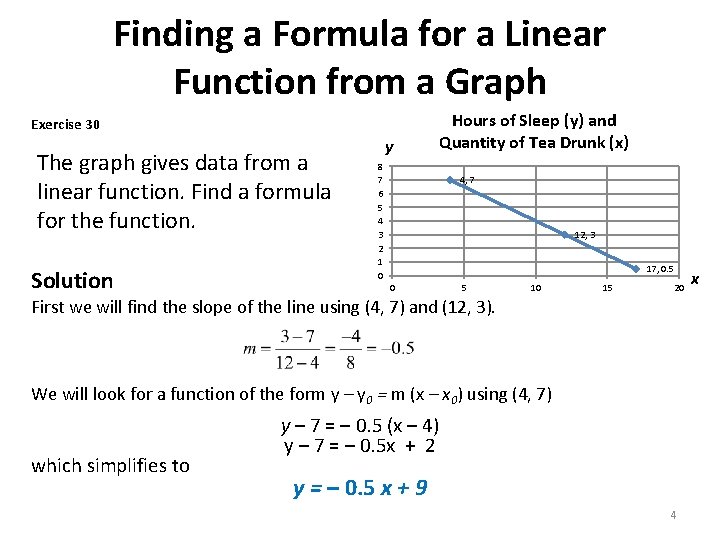
Finding a Formula for a Linear Function from a Graph Exercise 30 The graph gives data from a linear function. Find a formula for the function. Solution y Hours of Sleep (y) and Quantity of Tea Drunk (x) 8 7 6 5 4 3 2 1 0 4, 7 12, 3 17, 0. 5 0 5 10 15 20 First we will find the slope of the line using (4, 7) and (12, 3). We will look for a function of the form y – y 0 = m (x – x 0) using (4, 7) which simplifies to y – 7 = – 0. 5 (x – 4) y – 7 = – 0. 5 x + 2 y = – 0. 5 x + 9 4 x

Finding a Formula for a Linear Function from a Verbal Description Example 3 We have $24 to spend on soda and chips for a party. A six-pack of soda costs $3 and a bag of chips costs $2. The number of six-packs we can afford, s, is a function of the number of bags of chips we decide to buy, c. (a) Find an equation relating s and c. Solution • The amount of money ($) spent on soda will be 3 s. • The amount of money ($) spent on chips will be 2 c. • Assuming we spend all $24, the equation becomes: 2 c + 3 s = 24 3 s = -2 c + 24 5 s = – 2/3 c + 8

Interpreting a Formula for a Linear Function from a Verbal Description Example 3 From (a), the equation is (b) Graph the equation. Interpret the intercepts and the slope in the context of the party. Solution The fact that m = − 2/3 means that for each additional bag of chips purchased, we can purchase 2/3 fewer sixpacks of soda. Soda Versus Chips All soda 8 No chips 6 packs of soda and 4 bags of chips 4 All chips No soda 0 0 6 12 6

Alternative Forms for the Equation of a Line • The slope-intercept form is y = mx + b where m is the slope and b is the y-intercept. • The point-slope form is y − y 0 = m(x − x 0) where m is the slope and (x 0, y 0) is a point on the line. • The standard form is Ax + By + C = 0 where A, B, and C are constants. 7