1 4 Equations of Lines and Linear Models











- Slides: 17

1. 4 Equations of Lines and Linear Models Point-Slope Form The line with slope m passing through the point (x 1, y 1) has equation Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -1

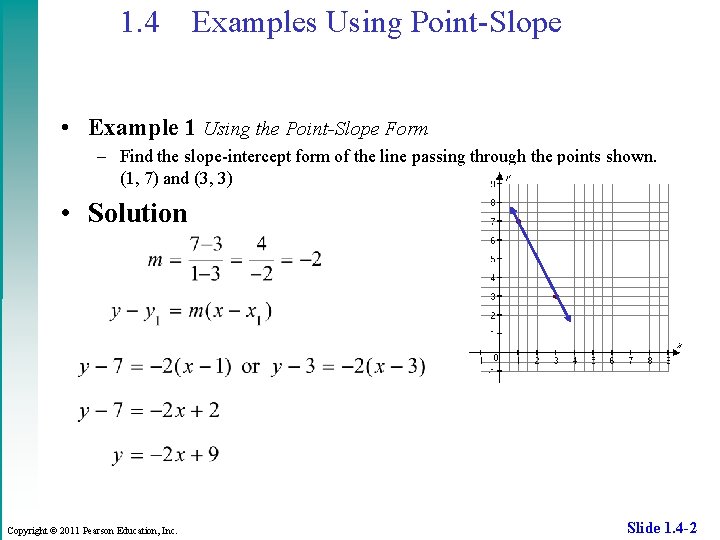
1. 4 Examples Using Point-Slope • Example 1 Using the Point-Slope Form – Find the slope-intercept form of the line passing through the points shown. (1, 7) and (3, 3) • Solution Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -2

1. 4 Examples Using Point-Slope • Example 2 Using the Point-Slope Form – The table below shows a list of points found on the line Find the equation of the line. Solution Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -3

1. 4 Standard Form of the Equation of a Line Standard Form A linear equation written in the form where A, B, and C are real numbers, is said to be in standard form. Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -4

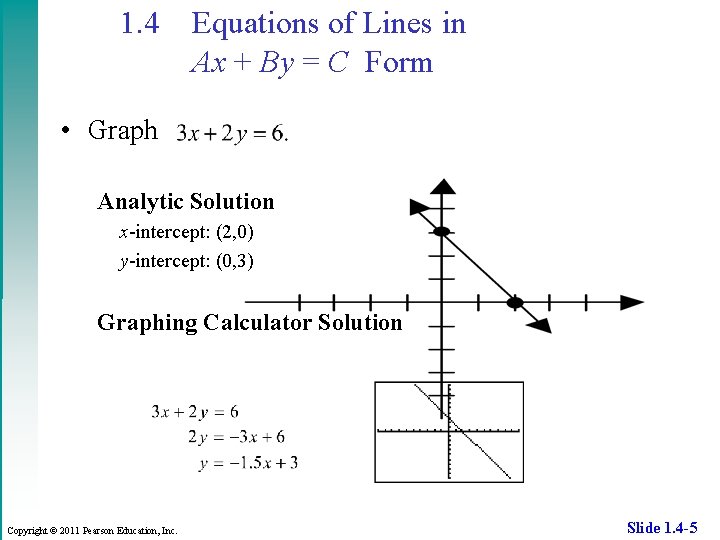
1. 4 Equations of Lines in Ax + By = C Form • Graph Analytic Solution x-intercept: (2, 0) y-intercept: (0, 3) Graphing Calculator Solution Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -5

1. 4 Parallel Lines Two distinct nonvertical lines are parallel if and only if they have the same slope. Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -6

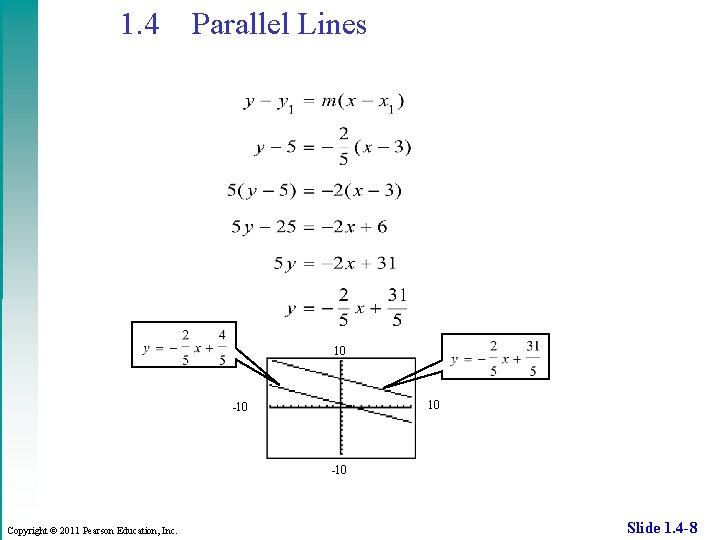
1. 4 Parallel Lines Example Find the equation of the line that passes through the point (3, 5) and is parallel to the line with equation Graph both lines in the standard viewing window. Solution Copyright © 2011 Pearson Education, Inc. Solve for y in terms of x. Slide 1. 4 -7

1. 4 Parallel Lines 10 10 -10 Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -8

1. 4 Perpendicular Lines Two lines, neither of which is vertical, are perpendicular if and only if their slopes have product – 1. Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -9

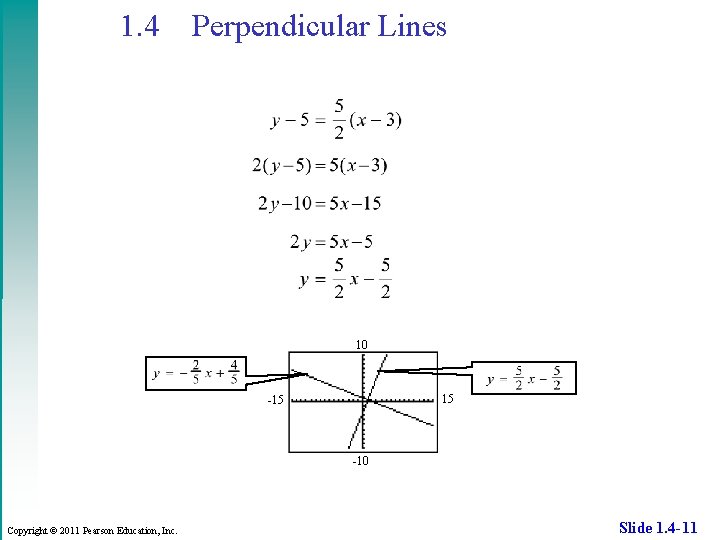
1. 4 Perpendicular Lines Example Find the equation of the line that passes through the point (3, 5) and is perpendicular to the line with equation Graph both lines in the standard viewing window. Use slope from the previous example. The slope of a perpendicular line is Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -10

1. 4 Perpendicular Lines 10 15 -10 Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -11

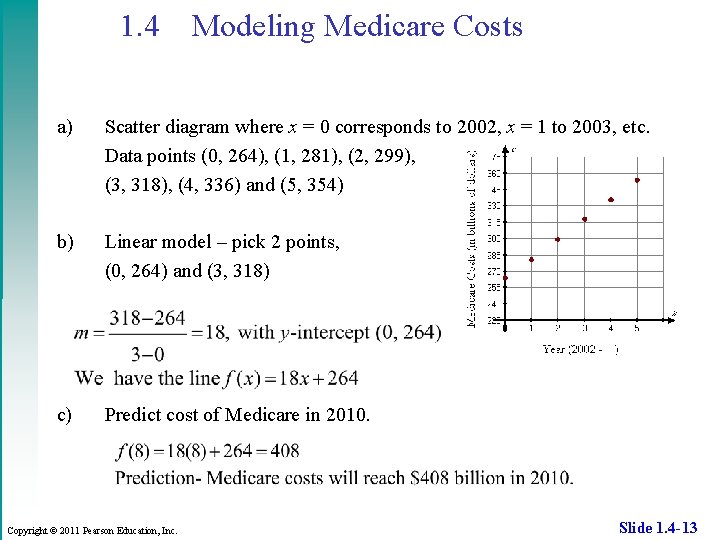
1. 4 Modeling Medicare Costs • Linear Models and Regression – Discrete data points can be plotted and the graph is called a scatter diagram. – Useful when analyzing trends in data. – e. g. Estimates for Medicare costs (in billions) Copyright © 2011 Pearson Education, Inc. x (Year) y (Cost) 2002 264 2003 281 2004 299 2005 318 2006 336 2007 354 Slide 1. 4 -12

1. 4 Modeling Medicare Costs a) Scatter diagram where x = 0 corresponds to 2002, x = 1 to 2003, etc. Data points (0, 264), (1, 281), (2, 299), (3, 318), (4, 336) and (5, 354) b) Linear model – pick 2 points, (0, 264) and (3, 318) c) Predict cost of Medicare in 2010. Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -13

1. 4 The Least-Squares Regression Line – Enter data into lists L 1 (x list) and L 2 (y list) – Least-squares regression line: Lin. Reg in STAT/CALC menu Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -14

1. 4 Correlation Coefficient • Correlation Coefficient r – Determines if a linear model is appropriate • range of r: • r near +1, low x-values correspond to low y-values and high x-values correspond to high y-values. • r near – 1, low x-values correspond to high y-values and high x-values correspond to low y-values. • means there is little or no correlation. – To calculate r using the TI-83, turn Diagnostic On in the Catalog menu. Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -15

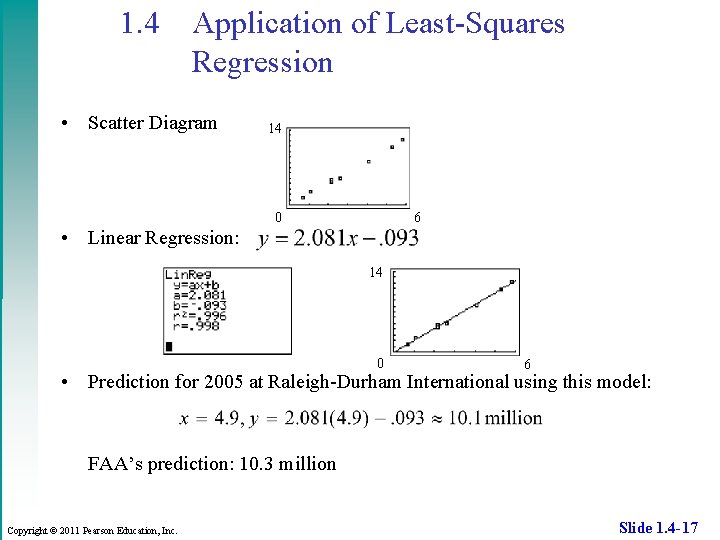
1. 4 Application of Least-Squares Regression • Example Predicting the Number of Airline Passengers (millions) Airport Copyright © 2011 Pearson Education, Inc. 1992 2005 Harrisburg International 0. 7 1. 4 Dayton International 1. 1 2. 4 Austin Robert Mueller 2. 2 4. 7 Milwaukee General Mitchell 2. 2 4. 4 Sacramento Metropolitan 2. 6 5. 0 Fort Lauderdale-Hollywood 4. 1 8. 1 Washington Dulles 5. 3 10. 9 Greater Cincinnati 5. 8 12. 3 Slide 1. 4 -16

1. 4 Application of Least-Squares Regression • Scatter Diagram 14 0 6 • Linear Regression: 14 0 6 • Prediction for 2005 at Raleigh-Durham International using this model: FAA’s prediction: 10. 3 million Copyright © 2011 Pearson Education, Inc. Slide 1. 4 -17