1 4 Absolute Values Solving Absolute Value Equations

1. 4 Absolute Values Solving Absolute Value Equations By putting into one of 3 categories

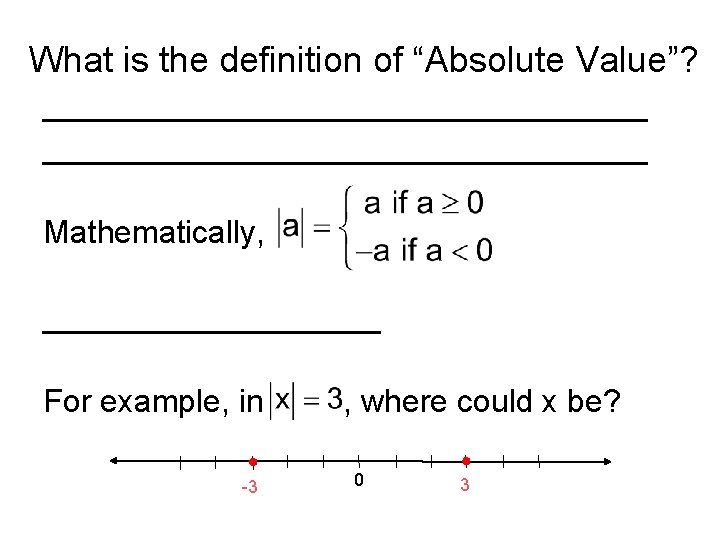
What is the definition of “Absolute Value”? __________________________________ Mathematically, __________ For example, in -3 , where could x be? 0 3

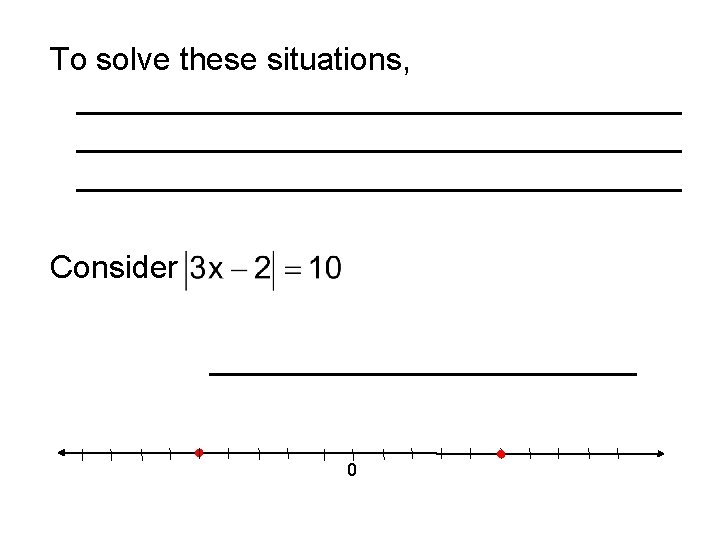
To solve these situations, __________________________________ Consider ____________ 0

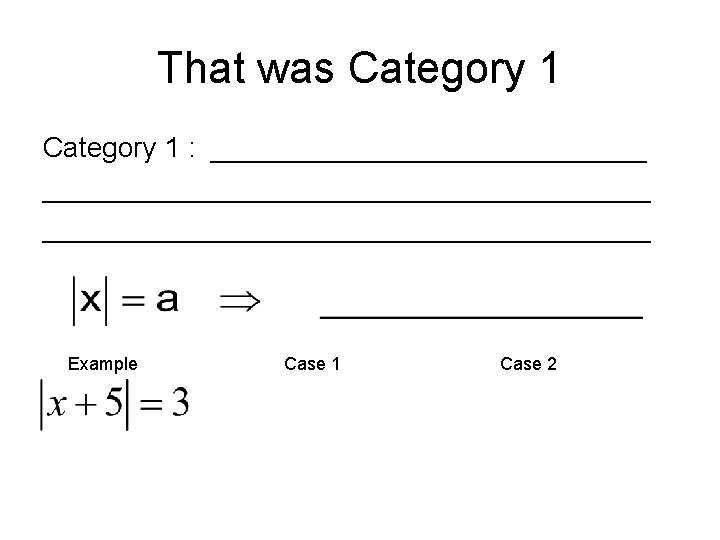
That was Category 1 : __________________________________ Example Case 1 Case 2

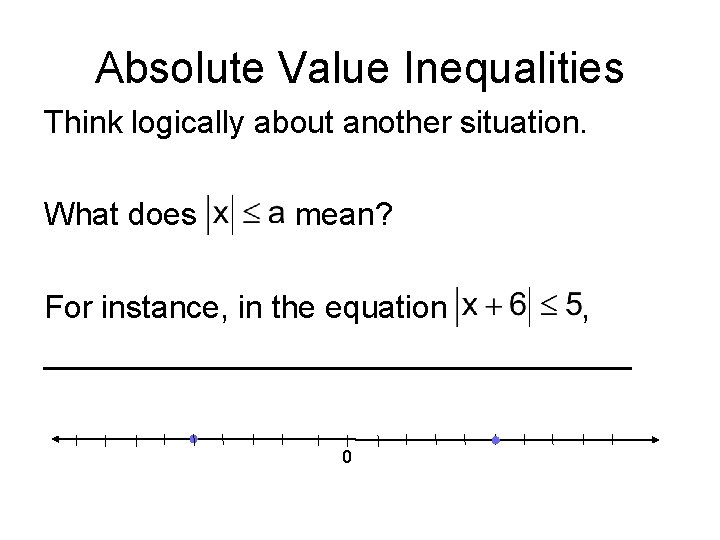
Absolute Value Inequalities Think logically about another situation. What does mean? For instance, in the equation , _________________ 0

How does that translate into a sentence? _________________ Now solve for x. This is Category 2: when x is less than a number

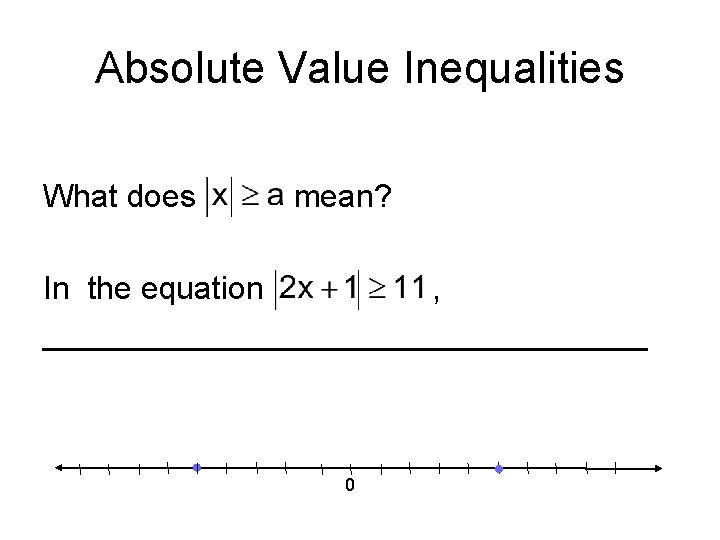
Absolute Value Inequalities What does mean? In the equation , _________________ 0

Less than = And statement Greater than = Or statement Note: is the same as ; just have the sign in the rewritten equation match the original.

Example inequality with x on other side Case 1 Case 2

Examples Case 1 Case 2

Case 1 Case 2

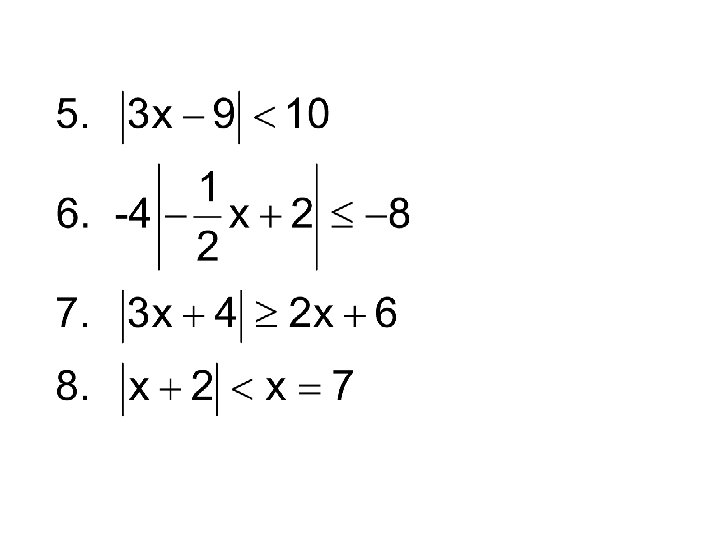
1 -4 Compound Absolute Values Equalities and Inequalities More than one absolute value in the equation

Find a number that works. We will find a more methodical approach to find all the solutions.

In your approach, think about the values of this particular mathematical statement in the 3 different areas on a number line. _____________________ -____________________ - ____________________

It now forms 3 different areas or cases on the number line. • ______________________________ • __________________

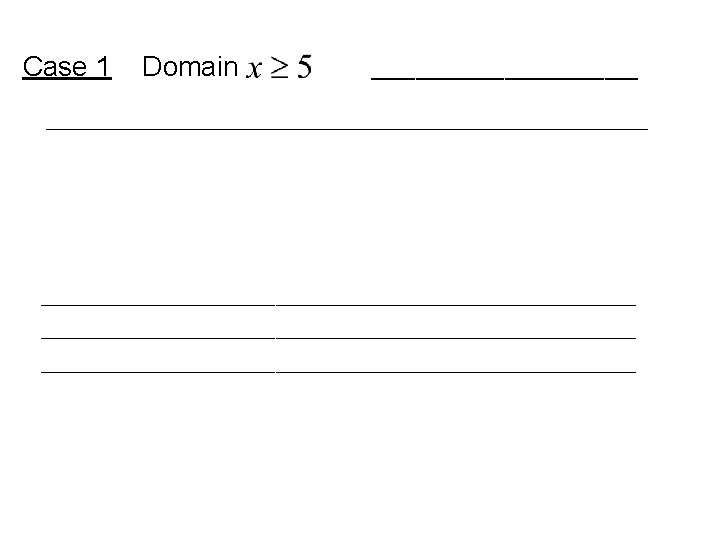
Case 2 Domain __________________

Case 3 Domain _______________

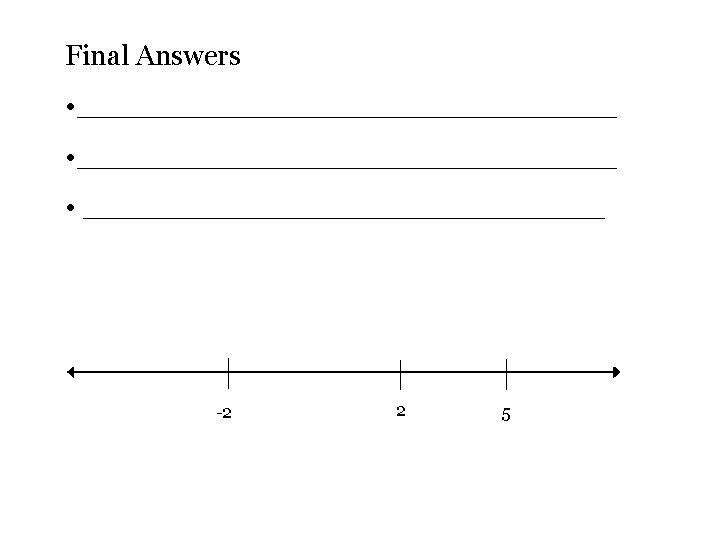
If you get an answer in any of the cases where the variable disappears and the answer is TRUE ________________________________

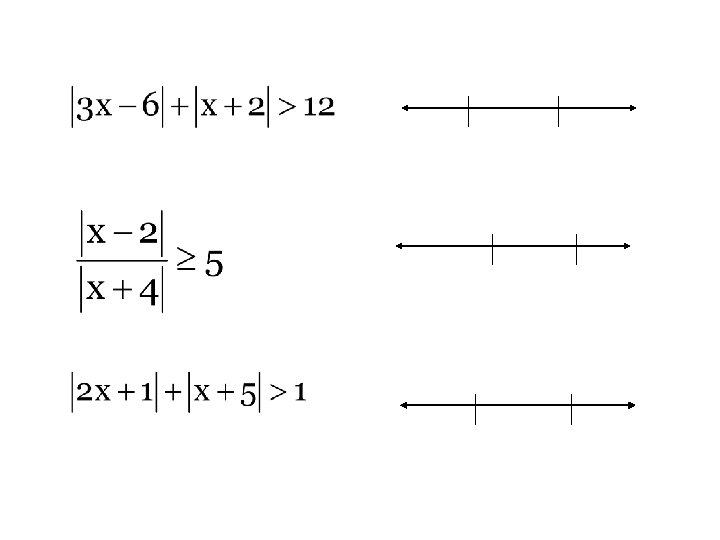
1 -5 Exponential Rules You know these already

Review of the Basics

Practice problems Simplify each expression

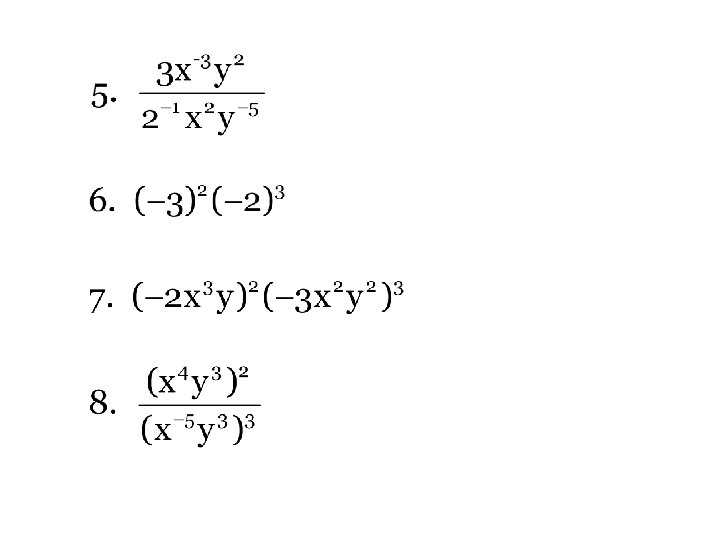
Do NOT use calculators on the homework, please!!

1 -6 Radicals (Day 1) and Rational Exponents (Day 2)

What is a Radical? In simplest term, it is a square root ( = ________ )

The Principle nth root of a: 1. • If a < 0 and n is odd then is a negative number __________ • If a < 0 and n is even, _______

Vocab

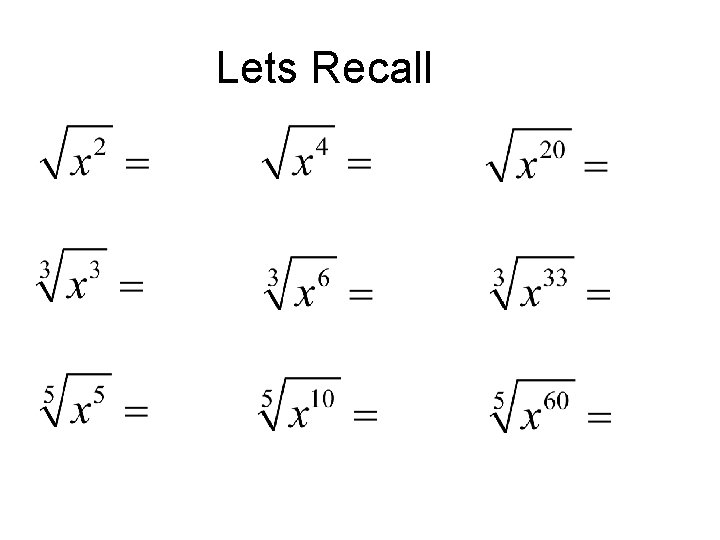
Lets Recall

Rules of Radicals

Practice problems Simplify each expression

1 -6 Radicals (Day 1) and Rational Exponents (Day 2)

What is a Rational Exponent? ____________________________________

$Don’t be overwhelmed by fractions! These problems are not hard, as long as you$

Don’t be overwhelmed by fractions! These problems are not hard, as long as you remember what each letter means. Notice I used “p” as the numerator and “r” as the denominator. p= _______________ r= ________________________________________

Practice problems Simplify each expression

The last part of this topic What is wrong with this number? ___________________________________

Rationalizing If you see a single radical in the denominator ________________________________________

Rationalizing If you see 1 or more radicals in a binomial, what can we do?

What is a Conjugate? The conjugate of a + b ______. Why? The conjugate ___________________________________

Rationalizing Multiply top and bottom by the conjugate! Its MAGIC!!

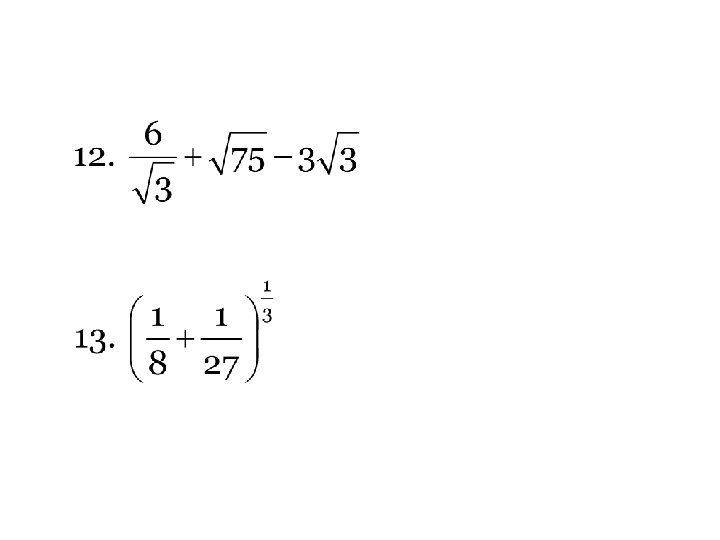
1. 7 Fundamental Operations

Terms • Monomial _______________ • Binomial ________________ • Trinomial _______________

Standard form: ____________________ Collecting Like terms

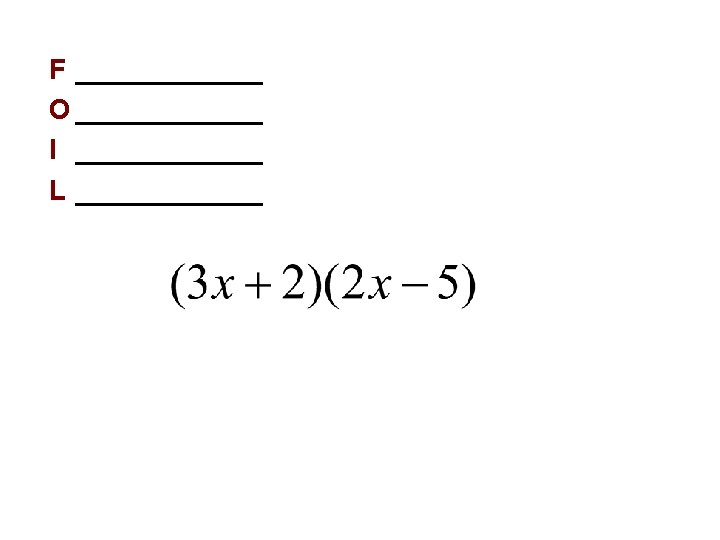
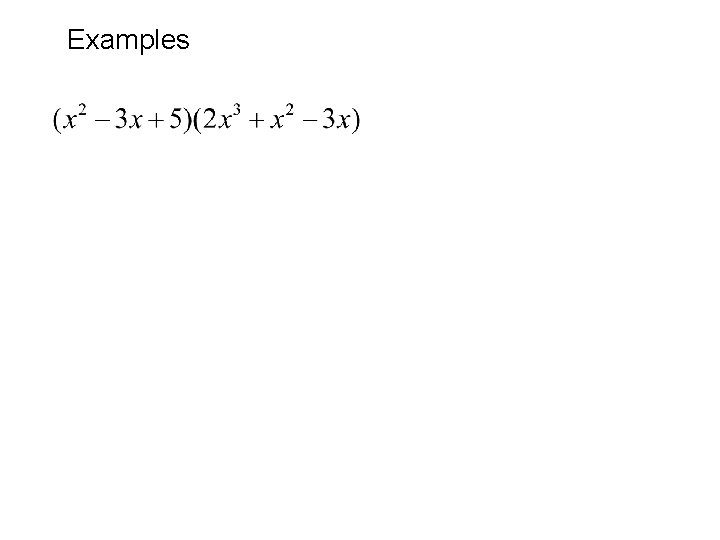
Examples

1 -8 Factoring Patterns

Perfect Square Trinomial Factors as

Difference of squares

Sum/Difference of cubes

3 terms but not a pattern? This is where you use combinations of the first term with combinations of the third term that collect to be the middle term.

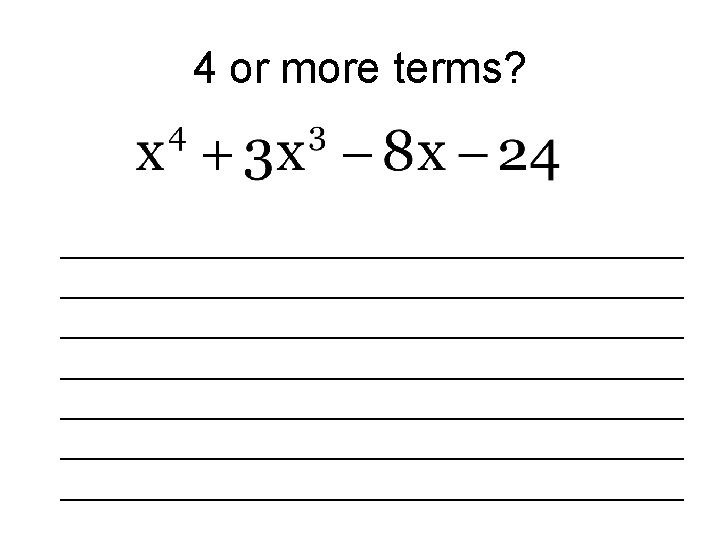
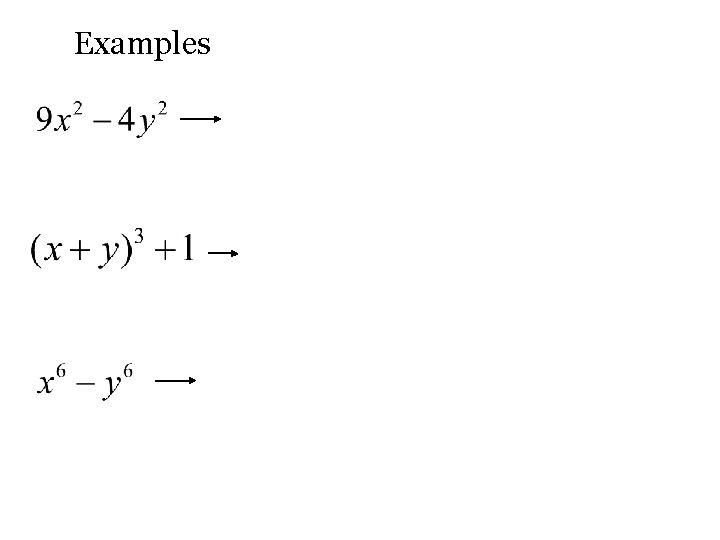
Examples

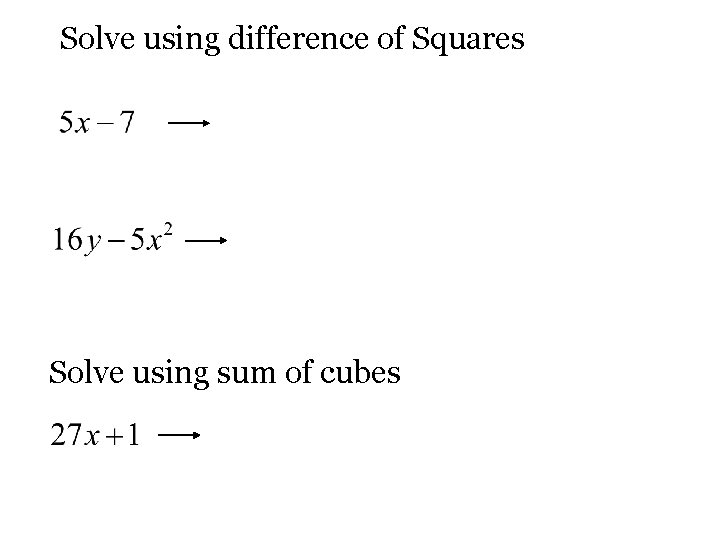
Solve using difference of Squares Solve using sum of cubes

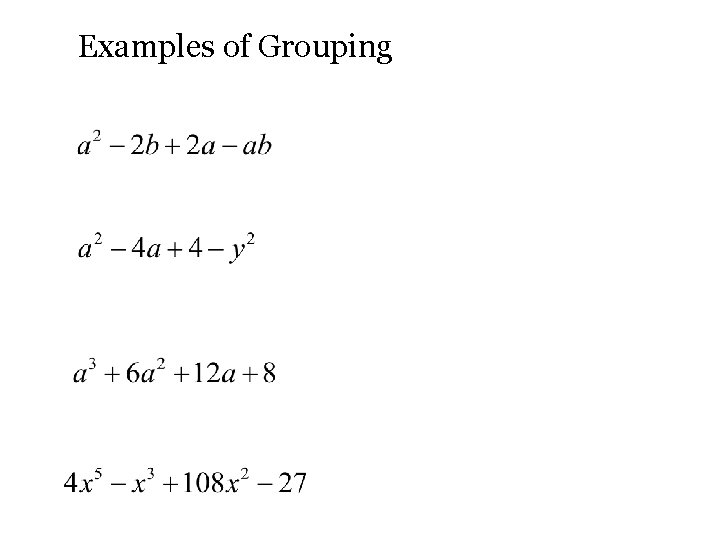
Examples of Grouping

1. 9 Fundamental Operations What are the Fundamental Operations?

Addition, Subtraction, Multiplication and Division We will be applying these fundamental operations to rational expressions. This will all be review. We are working on the little things here.

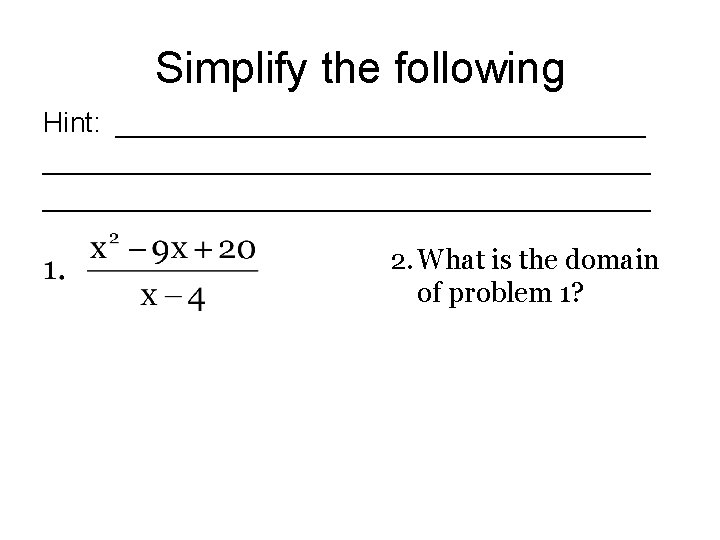
Simplify the following Hint: _______________________________________ 2. What is the domain of problem 1?

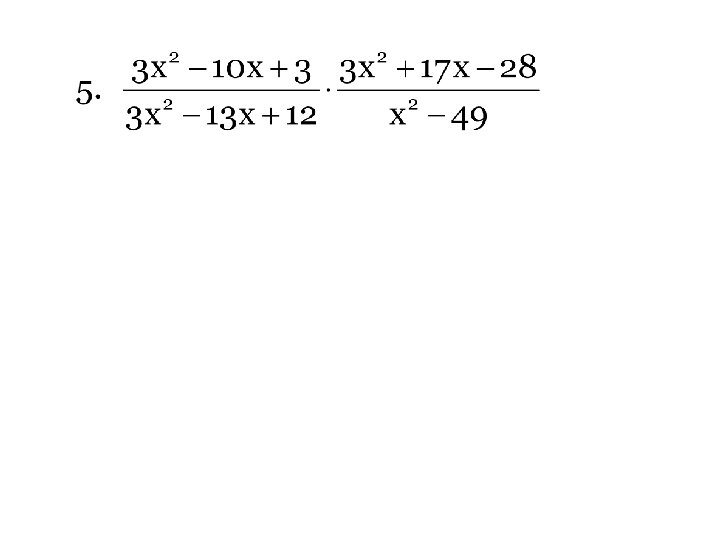
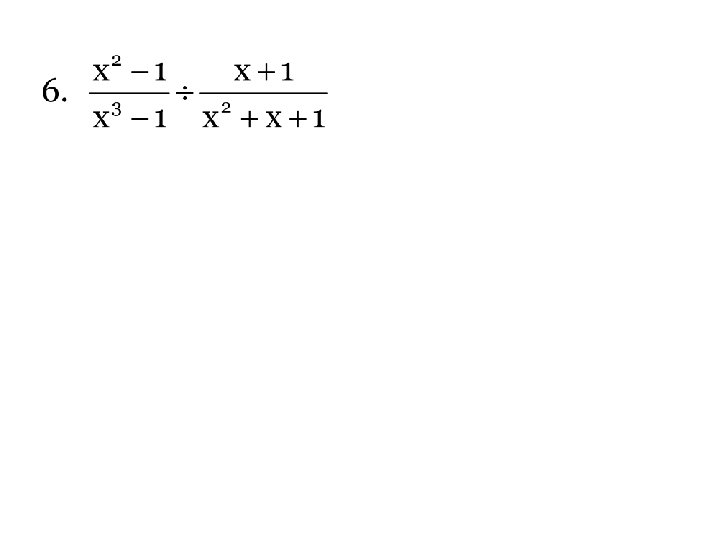
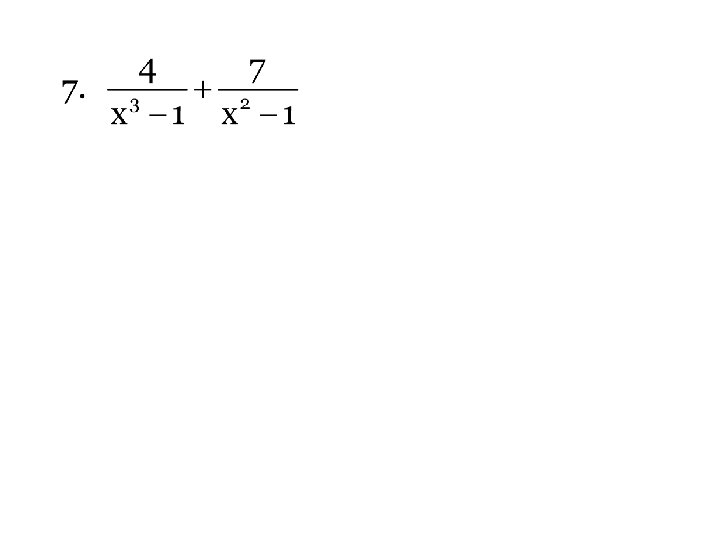
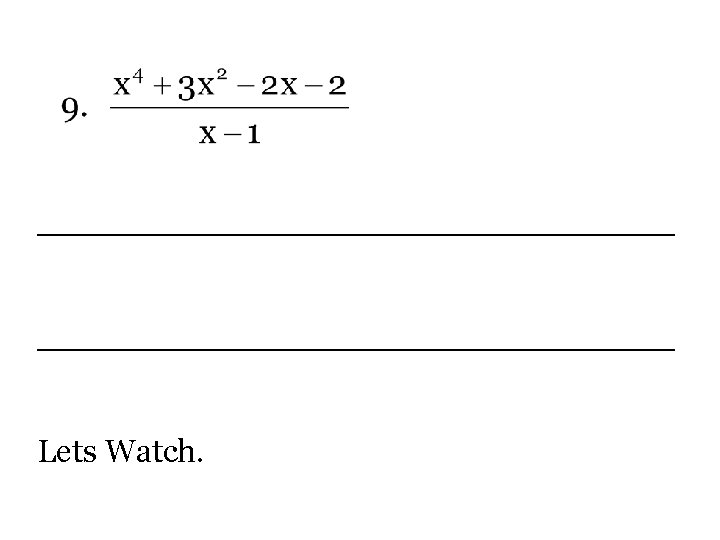
Polynomial Long Division

Classwork

1 -10 Introduction to Complex Numbers What is a complex number?

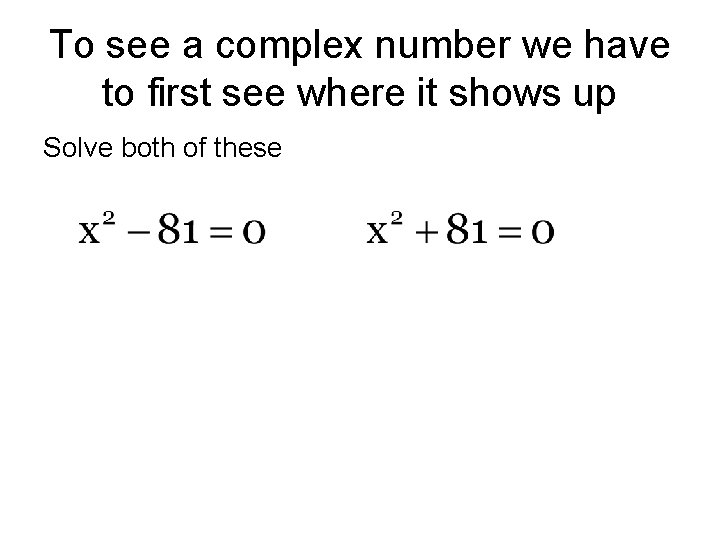
To see a complex number we have to first see where it shows up Solve both of these

Um, no solution? ? does not have a real answer. It has an “imaginary” answer. To define a complex number ________________________ This new variable is “ i “

Definition: Note: _________ So, following this definition: ______________________________

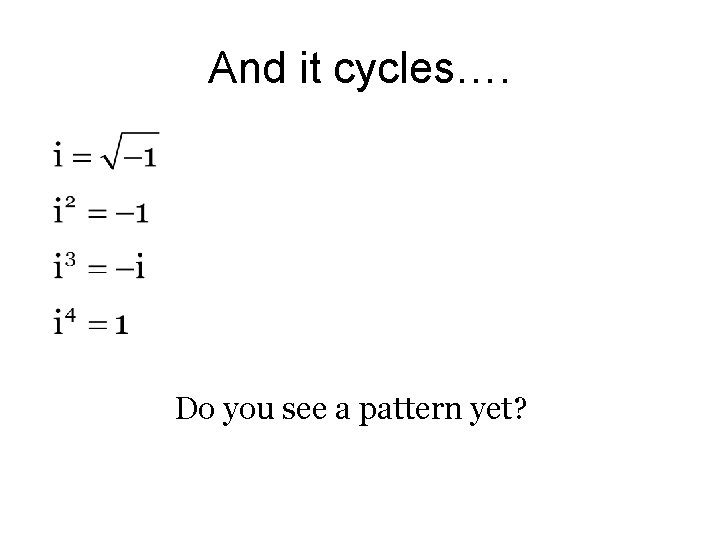
And it cycles…. Do you see a pattern yet?

What is that pattern? We are looking at the remainder when the power is divided by 4. Why? ___________________________________ Try it with

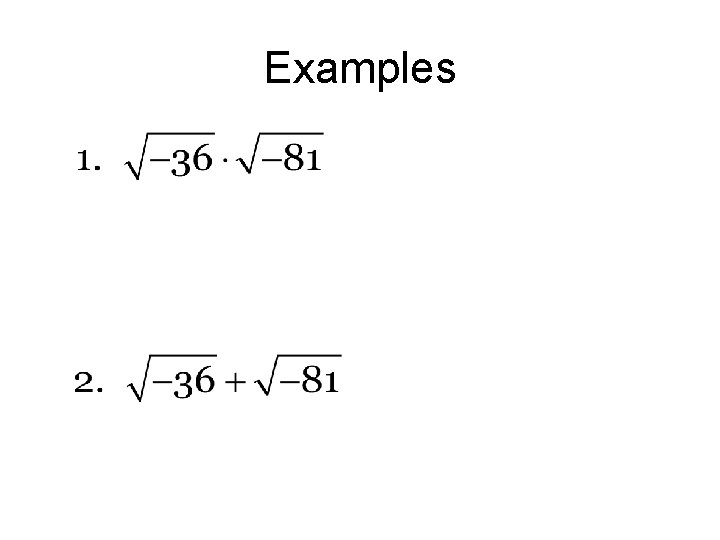
Examples

OK, so what is a complex number? ______________________________ A complex number comes in the form a + bi

Lets try these 4 problems.

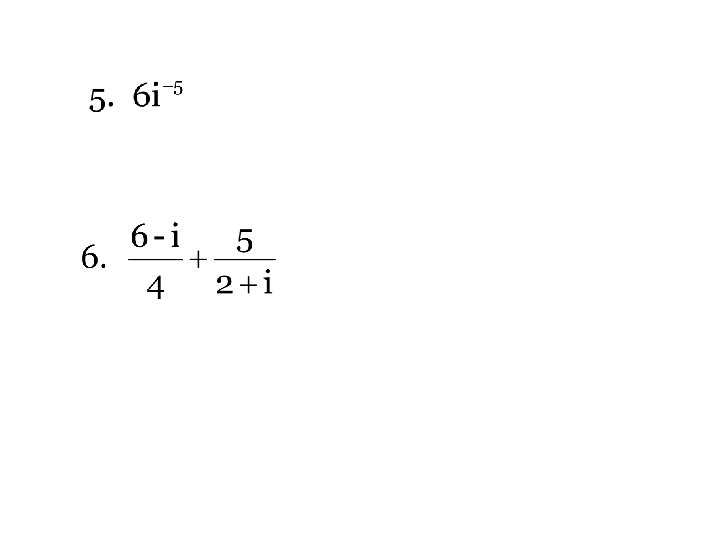
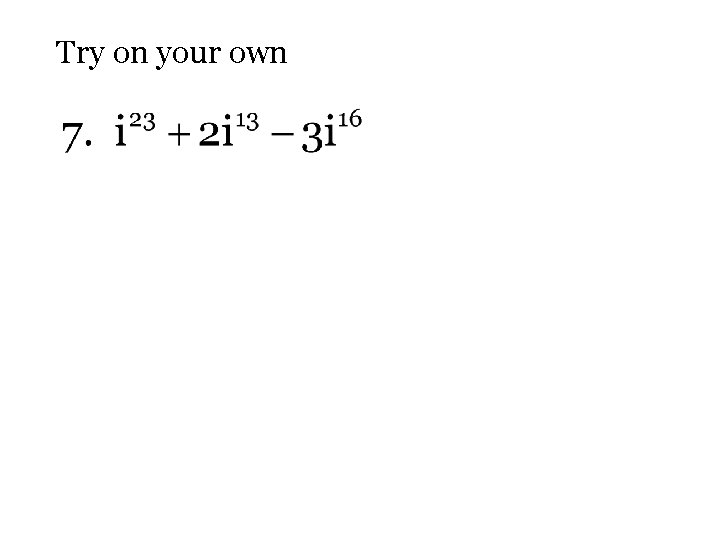
Try on your own