1 3 Vectors and resolution of forces Scalar

1. 3 Vectors and resolution of forces • Scalar and vector quantities • Manipulation of vectors • Forces in equilibrium © Manhattan Press (H. K. ) Ltd. 1

1. 3 Vectors and resolution of forces (SB p. 47) Scalar and vector quantities 1. Scalar quantities A scalar quantity is one which can be described fully by just stating its magnitude. e. g. mass, time, length, temperature, density, speed, energy, volume © Manhattan Press (H. K. ) Ltd. 2

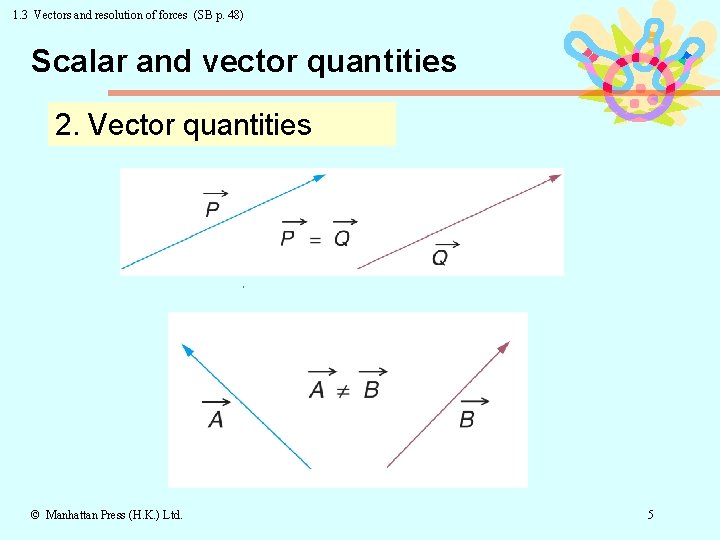
1. 3 Vectors and resolution of forces (SB p. 48) Scalar and vector quantities 2. Vector quantities A vector quantity is one which can only be fully described if its magnitude and direction are stated. e. g. displacement, velocity, acceleration, force, momentum, magnetic flux, electric intensity © Manhattan Press (H. K. ) Ltd. 3

1. 3 Vectors and resolution of forces (SB p. 48) Scalar and vector quantities 2. Vector quantities Represented by: © Manhattan Press (H. K. ) Ltd. 4

1. 3 Vectors and resolution of forces (SB p. 48) Scalar and vector quantities 2. Vector quantities © Manhattan Press (H. K. ) Ltd. 5

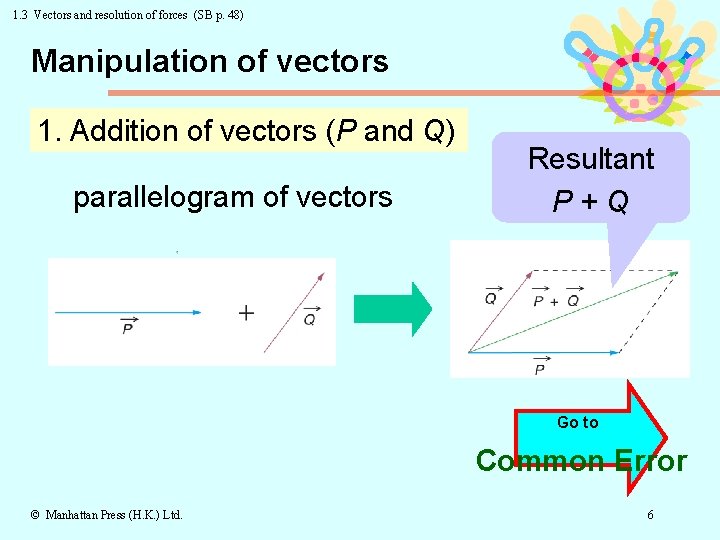
1. 3 Vectors and resolution of forces (SB p. 48) Manipulation of vectors 1. Addition of vectors (P and Q) parallelogram of vectors Resultant P+Q Go to Common Error © Manhattan Press (H. K. ) Ltd. 6

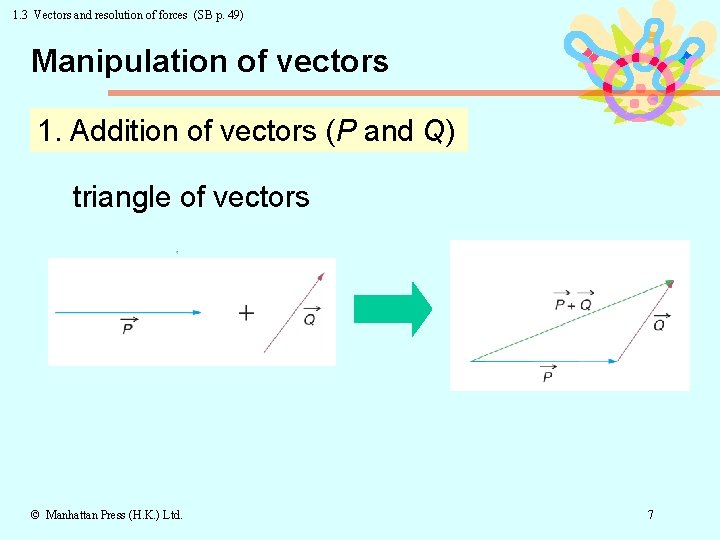
1. 3 Vectors and resolution of forces (SB p. 49) Manipulation of vectors 1. Addition of vectors (P and Q) triangle of vectors © Manhattan Press (H. K. ) Ltd. 7

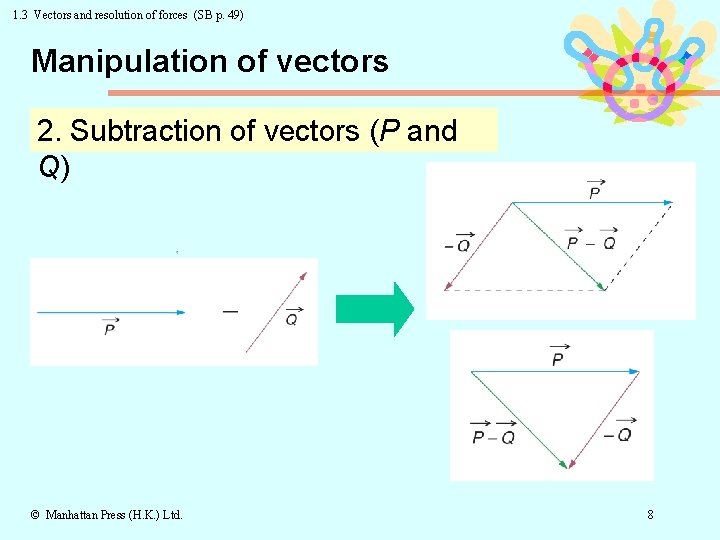
1. 3 Vectors and resolution of forces (SB p. 49) Manipulation of vectors 2. Subtraction of vectors (P and Q) © Manhattan Press (H. K. ) Ltd. 8

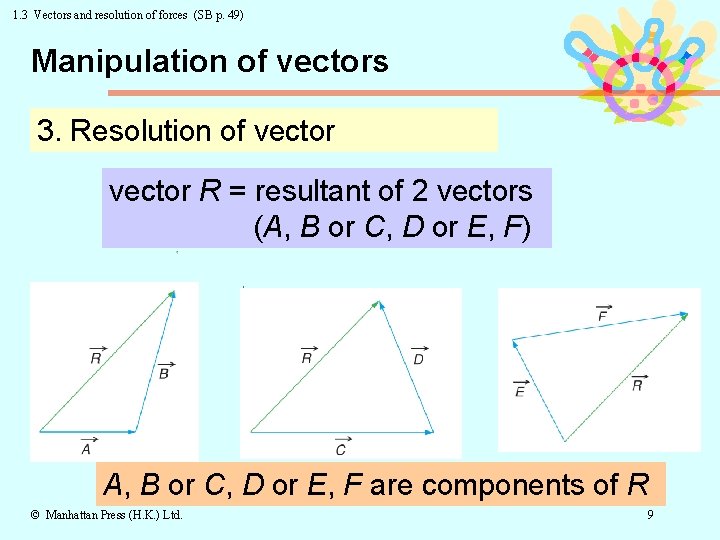
1. 3 Vectors and resolution of forces (SB p. 49) Manipulation of vectors 3. Resolution of vector R = resultant of 2 vectors (A, B or C, D or E, F) A, B or C, D or E, F are components of R © Manhattan Press (H. K. ) Ltd. 9

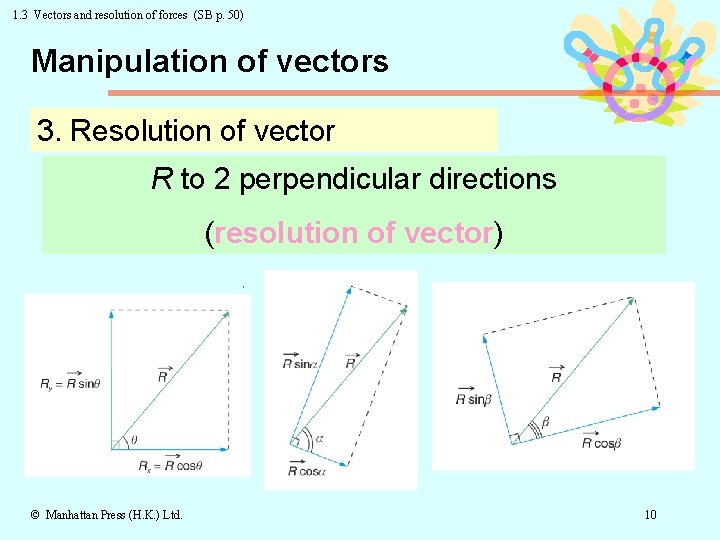
1. 3 Vectors and resolution of forces (SB p. 50) Manipulation of vectors 3. Resolution of vector R to 2 perpendicular directions (resolution of vector) © Manhattan Press (H. K. ) Ltd. 10

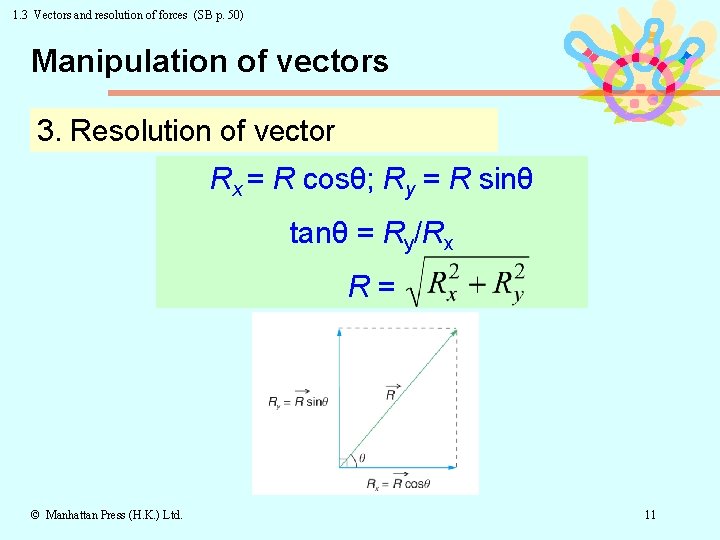
1. 3 Vectors and resolution of forces (SB p. 50) Manipulation of vectors 3. Resolution of vector Rx = R cosθ; Ry = R sinθ tanθ = Ry/Rx R= © Manhattan Press (H. K. ) Ltd. 11

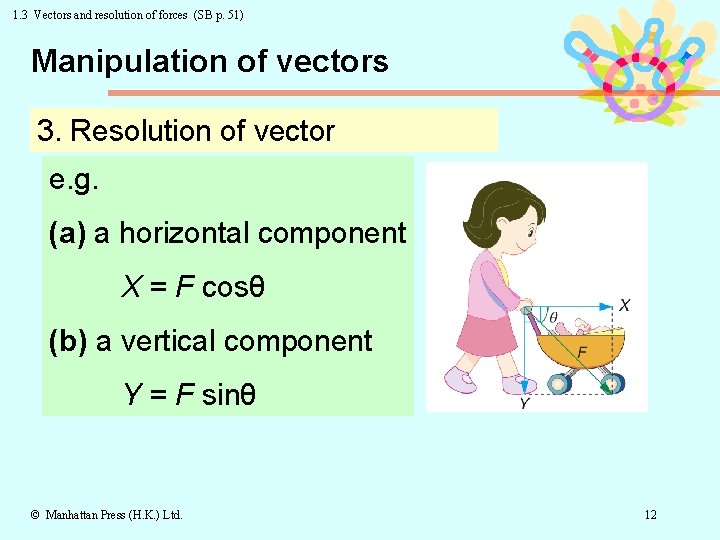
1. 3 Vectors and resolution of forces (SB p. 51) Manipulation of vectors 3. Resolution of vector e. g. (a) a horizontal component X = F cosθ (b) a vertical component Y = F sinθ © Manhattan Press (H. K. ) Ltd. 12

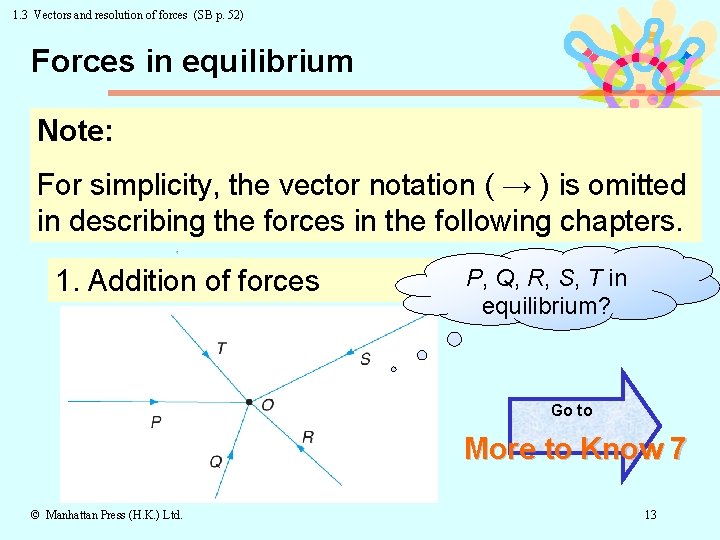
1. 3 Vectors and resolution of forces (SB p. 52) Forces in equilibrium Note: For simplicity, the vector notation ( → ) is omitted in describing the forces in the following chapters. 1. Addition of forces P, Q, R, S, T in equilibrium? Go to More to Know 7 © Manhattan Press (H. K. ) Ltd. 13

1. 3 Vectors and resolution of forces (SB p. 53) Forces in equilibrium 1. Addition of forces The polygon of forces states that if the forces acting on a point can be represented in magnitude and direction by the sides of a polygon, then the forces are in equilibrium. In equilibrium (can form polygon) © Manhattan Press (H. K. ) Ltd. 14

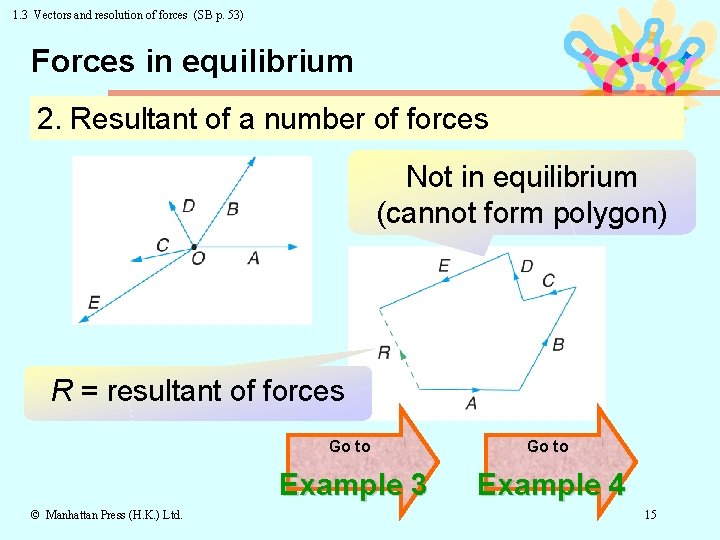
1. 3 Vectors and resolution of forces (SB p. 53) Forces in equilibrium 2. Resultant of a number of forces Not in equilibrium (cannot form polygon) R = resultant of forces © Manhattan Press (H. K. ) Ltd. Go to Example 3 Example 4 15

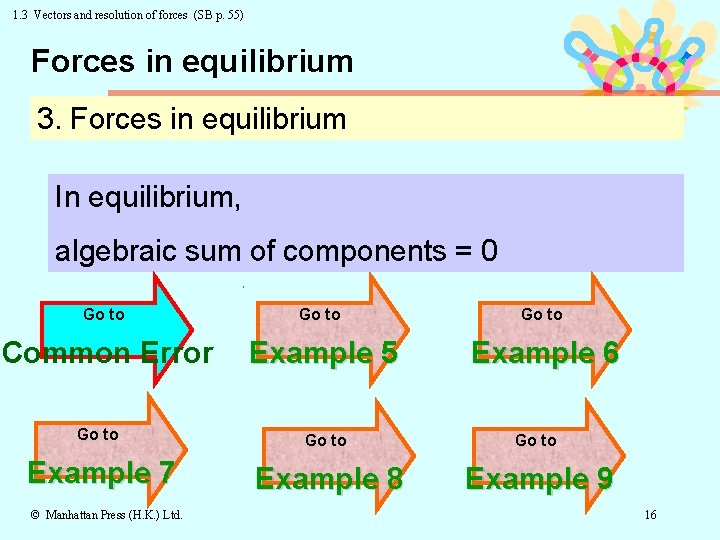
1. 3 Vectors and resolution of forces (SB p. 55) Forces in equilibrium 3. Forces in equilibrium In equilibrium, algebraic sum of components = 0 Go to Common Error Example 5 Example 6 Go to Example 7 Example 8 Example 9 © Manhattan Press (H. K. ) Ltd. 16

End © Manhattan Press (H. K. ) Ltd. 17

1. 3 Vectors and resolution of forces (SB p. 48) The magnitude of the resultant force is not necessarily greater than those of its components of forces. Return to © Manhattan Press (H. K. ) Ltd. Text 18

1. 3 Vectors and resolution of forces (SB p. 52) Concurrent & coplanar forces The forces shown in Fig. 1. 22(a) are concurrent and coplanar forces. When the force vectors all intersect at one point, the forces are known as concurrent. When the problem involves forces in two dimensions only, the forces are said to be coplanar as they all lie on the same plane. Return to © Manhattan Press (H. K. ) Ltd. Text 19

1. 3 Vectors and resolution of forces (SB p. 54) Q: The forces acting on a point O are shown in the figure below. Find the magnitude and direction of the resultant. Solution © Manhattan Press (H. K. ) Ltd. 20

1. 3 Vectors and resolution of forces (SB p. 54) Solution: Algebraic sum of components of forces along Ox, X = A cos 15° + B cos 30° + C cos 120° + D cos 225° = 4 cos 15° + 3 cos 30° + 3 cos 120° + 2 cos 225° = 3. 55 N Algebraic sum of components of forces along Oy, Y = 4 sin 15° + 3 sin 30° + 3 sin 120° + 2 sin 225° = 3. 72 N The magnitude of the resultant R= = 5. 14 N tanθ= ∴ θ= 46. 3° The resultant is 5. 14 N at an angle 46. 3° to the direction Ox. © Manhattan Press (H. K. ) Ltd. Return to Text 21

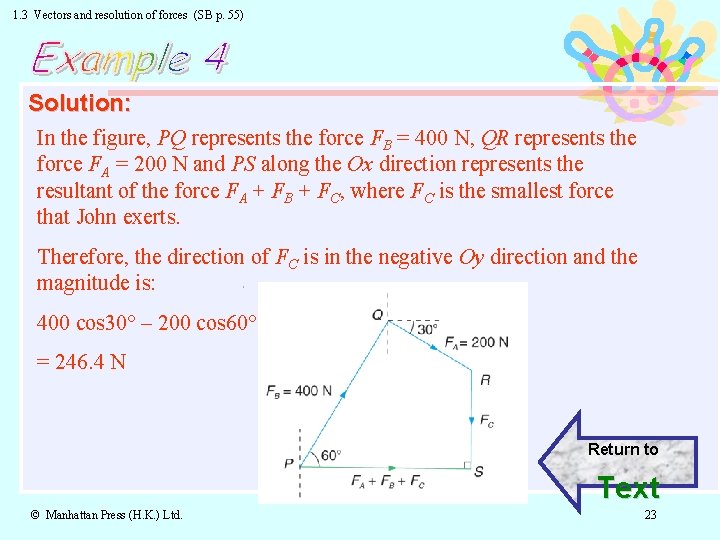
1. 3 Vectors and resolution of forces (SB p. 54) Q: Sam, Brian and John attempt to push an object in the direction Ox. Sam exerts a force of 200 N at a direction 30° to Ox, and Brian exerts a force of 400 N at 60° to Ox as shown in the figure. What are the magnitude and direction of the smallest force that John should exert such that the resultant of all three forces acts along Ox? Solution © Manhattan Press (H. K. ) Ltd. 22

1. 3 Vectors and resolution of forces (SB p. 55) Solution: In the figure, PQ represents the force FB = 400 N, QR represents the force FA = 200 N and PS along the Ox direction represents the resultant of the force FA + FB + FC, where FC is the smallest force that John exerts. Therefore, the direction of FC is in the negative Oy direction and the magnitude is: 400 cos 30° – 200 cos 60° = 246. 4 N Return to Text © Manhattan Press (H. K. ) Ltd. 23

1. 3 Vectors and resolution of forces (SB p. 55) Although the forces are in equilibrium, the object is not necessary to be in “static equilibrium”. We will learn the conditions for static equilibrium in Section 1. 5. Return to Text © Manhattan Press (H. K. ) Ltd. 24

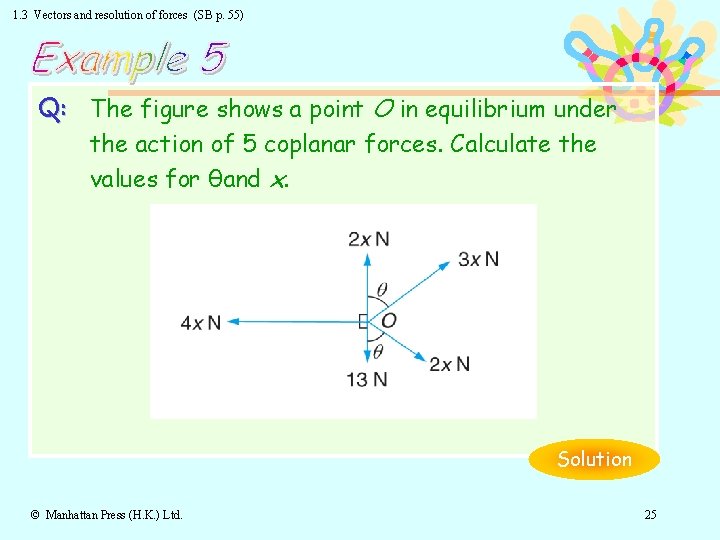
1. 3 Vectors and resolution of forces (SB p. 55) Q: The figure shows a point O in equilibrium under the action of 5 coplanar forces. Calculate the values for θand x. Solution © Manhattan Press (H. K. ) Ltd. 25

1. 3 Vectors and resolution of forces (SB p. 56) Solution: Since the forces are in equilibrium, the algebraic sum of the components of the forces in any direction is zero. Algebraic sum of components of forces along OX = 0 3 x sinθ + 2 x cos 90° + 4 x cos 180° + 13 cos 270° + 2 x sinθ = 0 5 x sinθ − 4 x = 0 sinθ = 4/5 θ = 53° 8’ Algebraic sum of components of forces along OY = 0 3 x cosθ + 2 x − 2 x cosθ − 13 = 0 2 x + x cosθ = 13 2 x + x (3/5) = 13 (13/5) x = 13 ∴x=5 Return to © Manhattan Press (H. K. ) Ltd. Text 26

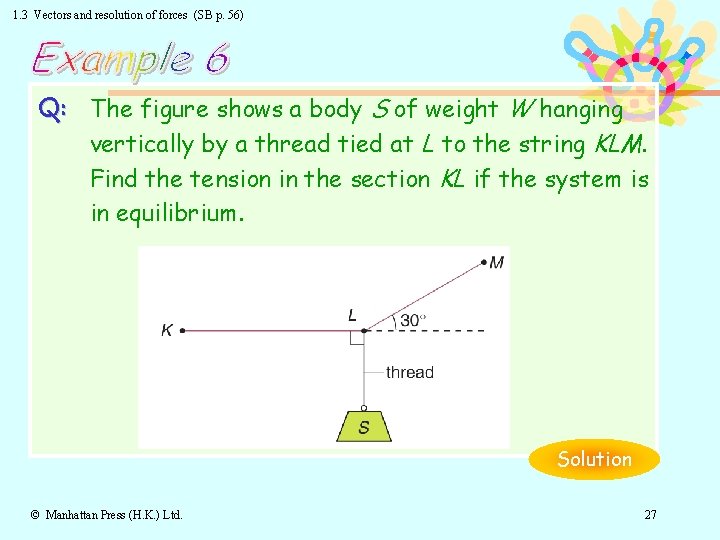
1. 3 Vectors and resolution of forces (SB p. 56) Q: The figure shows a body S of weight W hanging vertically by a thread tied at L to the string KLM. Find the tension in the section KL if the system is in equilibrium. Solution © Manhattan Press (H. K. ) Ltd. 27

1. 3 Vectors and resolution of forces (SB p. 56) Solution: Since the forces W, T and F are in equilibrium, the resultant of the three forces must be zero. Therefore, the algebraic sum of the components of the forces in any direction must be zero. Algebraic sum of components of forces along LX = 0. F cos 30° + (− T) = 0 F cos 30° − T = 0 T = F cos 30°. . . . (1) Algebraic sum of components of forces along LY = 0. F sin 30° + (− W) = 0 F sin 30° − W = 0 W = F sin 30°. . . . (2) (1)/(2) Return to Text © Manhattan Press (H. K. ) Ltd. 28

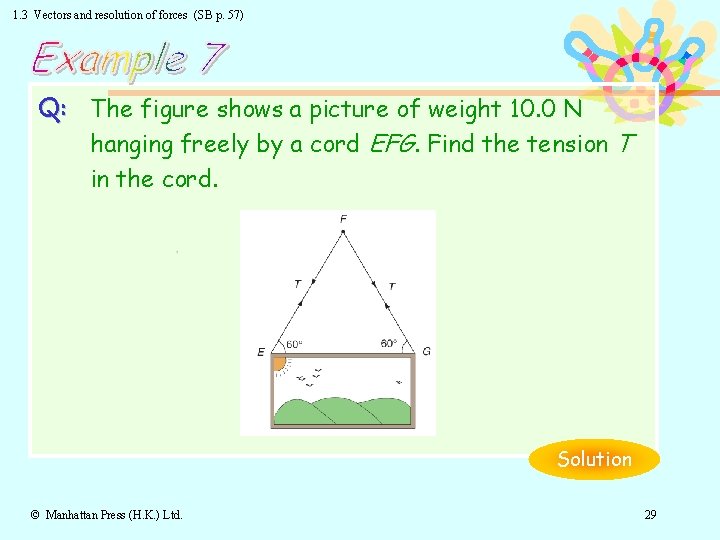
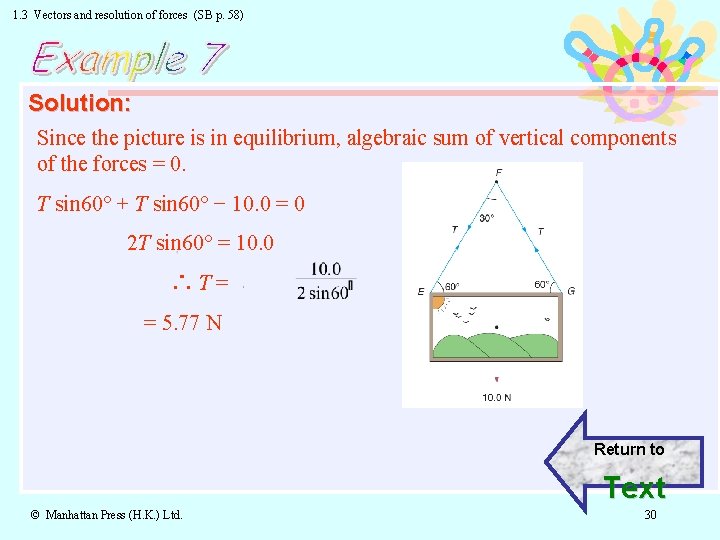
1. 3 Vectors and resolution of forces (SB p. 57) Q: The figure shows a picture of weight 10. 0 N hanging freely by a cord EFG. Find the tension T in the cord. Solution © Manhattan Press (H. K. ) Ltd. 29

1. 3 Vectors and resolution of forces (SB p. 58) Solution: Since the picture is in equilibrium, algebraic sum of vertical components of the forces = 0. T sin 60° + T sin 60° − 10. 0 = 0 2 T sin 60° = 10. 0 ∴T= = 5. 77 N Return to Text © Manhattan Press (H. K. ) Ltd. 30

1. 3 Vectors and resolution of forces (SB p. 58) Q: A mass of 5 kg hangs from two light strings of lengths 3 m and 4 m from two points at the same level and 5 m apart. Find the tension in each of the strings. (Assume g = 9. 81 m s− 2. ) Solution © Manhattan Press (H. K. ) Ltd. 31

1. 3 Vectors and resolution of forces (SB p. 59) Solution: Since the forces are in equilibrium, algebraic sum of the forces along CX = 0. T 2 sinθ − T 1 cosθ = 0 T 2 = . . . (1) Also, algebraic sum of the forces along CY = 0. T 2 cosθ + T 1 sinθ − W = 0 Substituting T 2 from (1), Return to Text © Manhattan Press (H. K. ) Ltd. 32

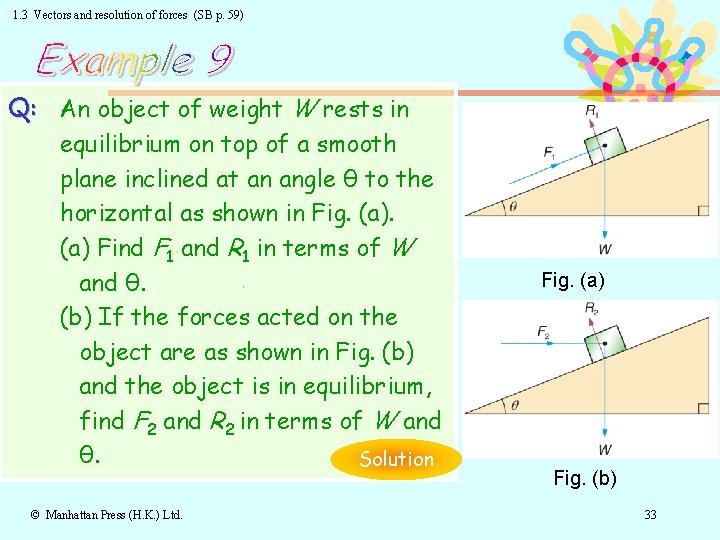
1. 3 Vectors and resolution of forces (SB p. 59) Q: An object of weight W rests in equilibrium on top of a smooth plane inclined at an angle θ to the horizontal as shown in Fig. (a) Find F 1 and R 1 in terms of W and θ. (b) If the forces acted on the object are as shown in Fig. (b) and the object is in equilibrium, find F 2 and R 2 in terms of W and θ. Solution © Manhattan Press (H. K. ) Ltd. Fig. (a) Fig. (b) 33

1. 3 Vectors and resolution of forces (SB p. 59) Solution: (a) Since the object is in equilibrium, algebraic sum of components of forces along the inclined plane = 0. F 1 + (− W sinθ) = 0 ∴ F 1 = W sinθ Algebraic sum of components of forces perpendicular to the inclined plane = 0. R 1 + (− W cosθ) = 0 ∴ R 1 = W cosθ Return to Text © Manhattan Press (H. K. ) Ltd. 34

1. 3 Vectors and resolution of forces (SB p. 60) Solution (cont’d): (b) Since the object is in equilibrium, algebraic sum of components of forces along the inclined plane = 0. F 2 cosθ + (−W sinθ) = 0 ∴ F 2 = = W tanθ Algebraic sum of components of forces perpendicular to the inclined plane = 0. R 2 + (−F 2 sinθ) + (−W cosθ) = 0 ∴ R 2 = F 2 sinθ + W cosθ Substituting F 2, © Manhattan Press (H. K. ) Ltd. = (W tanθ) sinθ + W cosθ Return to Text 35