1 3 Symbols and Sets of Numbers Definitions

1. 3 – Symbols and Sets of Numbers Definitions: Natural Numbers: {1, 2, 3, 4, …} Whole Numbers: All natural numbers plus zero, {0, 1, 2, 3, …} Equality Symbols

1. 4 – Symbols and Sets of Numbers Inequality Symbols

– Symbols and Sets of Numbers Equality and Inequality Symbols are used to create mathematical statements.

1. 4 – Symbols and Sets of Numbers Order Property for Real Numbers For any two real numbers, a and b, a is less than b if a is to the left of b on the number line. -92 -25 -11 0 1 12 43 67

1. 4 – Symbols and Sets of Numbers True or False

1. 4 – Symbols and Sets of Numbers Translating Sentences into Mathematical Statements Fourteen is greater than or equal to fourteen. Zero is less than five. Nine is not equal to ten. The opposite of five is less than or equal to negative two.

– Symbols and Sets of Numbers Identifying Common Sets of Numbers Definitions: Integers: All positive numbers, negative numbers and zero without fractions and decimals. {…, -3, -2, -1, 0, 1, 2, 3, 4, …}

– Symbols and Sets of Numbers Identifying Common Sets of Numbers Definitions: Rational Numbers: Any number that can be expressed as a quotient of two integers. Irrational Numbers: Any number that can not be expressed as a quotient of two integers.

9. 1 – Symbols and Sets of Numbers Real Numbers Irrational Rational Non-integer rational #s Integers Negative numbers Whole numbers Zero Natural numbers

– Symbols and Sets of Numbers Given the following set of numbers, identify which elements belong in each classification: Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers All elements

1. 4 – Properties of Real Numbers Commutative Properties Addition: Multiplication:

1. 4 – Properties of Real Numbers Associative Properties Addition: Multiplication:

1. 4 – Properties of Real Numbers Distributive Property of Multiplication

1. 4 – Properties of Real Numbers Identity Properties: Addition: 0 is the identity element for addition Multiplication: 1 is the identity element for multiplication

1. 4 – Properties of Real Numbers Additive Inverse Property: The numbers a and –a are additive inverses or opposites of each other if their sum is zero. Multiplicative Inverse Property: The numbers are reciprocals or multiplicative inverses of each other if their product is one.
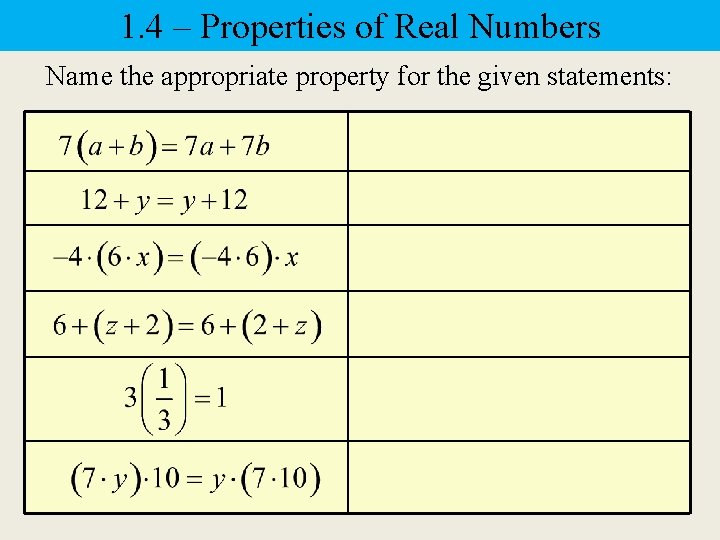
1. 4 – Properties of Real Numbers Name the appropriate property for the given statements:

- Slides: 17