1 3 Square Roots Warm Up Lesson Presentation

1 -3 Square Roots Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 2

1 -3 Square Roots Warm Up Round to the nearest tenth. 1. 3. 14 3. 1 2. 1. 97 2. 0 Find each square root. 3. 4 4. 25 Write each fraction in simplest form. 5. 6. Simplify. 7. Holt Mc. Dougal Algebra 2 8.

1 -3 Square Roots Objectives Estimate square roots. Simplify, add, subtract, multiply, and divide square roots. Holt Mc. Dougal Algebra 2

1 -3 Square Roots The side length of a square is the square root of its area. This relationship is shown by a radical symbol. The number or expression under the radical symbol is called the radicand. The radical symbol indicates only the positive square root of a number, called the principal root. To indicate both the positive and negative square roots of a number, use the plus or minus sign (±). or – 5 Holt Mc. Dougal Algebra 2

1 -3 Square Roots Numbers such as 25 that have integer square roots are called perfect squares. Square roots of integers that are not perfect squares are irrational numbers. You can estimate the value of these square roots by comparing them with perfect squares. For example, lies between and , so it lies between 2 and 3. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 1: Estimating Square Roots Estimate to the nearest tenth. < < 5< <6 Find the two perfect squares that 27 lies between. Find the two integers that lies between. Because 27 is closer to 25 than to 36, Try 5. 2: 5. 22 = 27. 04 5. 12 = 26. 01 Too high, try 5. 1. Too low Because 27 is closer to 27. 04 than 26. 01, than to 5. 1. Check On a calculator to the nearest tenth. Holt Mc. Dougal Algebra 2 is closer to 5 than to 6. is closer to 5. 2 ≈ 5. 1961524 ≈ 5. 1 rounded

1 -3 Square Roots Check It Out! Example 1 Estimate < – 7 < to the nearest tenth. < < – 8 Find the two perfect squares that – 55 lies between. Find the two integers that lies between –. Because – 55 is closer to – 49 than to – 64, is closer to – 7 than to – 8. Try 7. 2: 7. 22 = 51. 84 Too low, try 7. 42 = 54. 76 Too low but very close Because 55 is closer to 54. 76 than 51. 84, than to 7. 2. is closer to 7. 4 Check On a calculator ≈ – 7. 4161984 ≈ – 7. 4 rounded to the nearest tenth. Holt Mc. Dougal Algebra 2

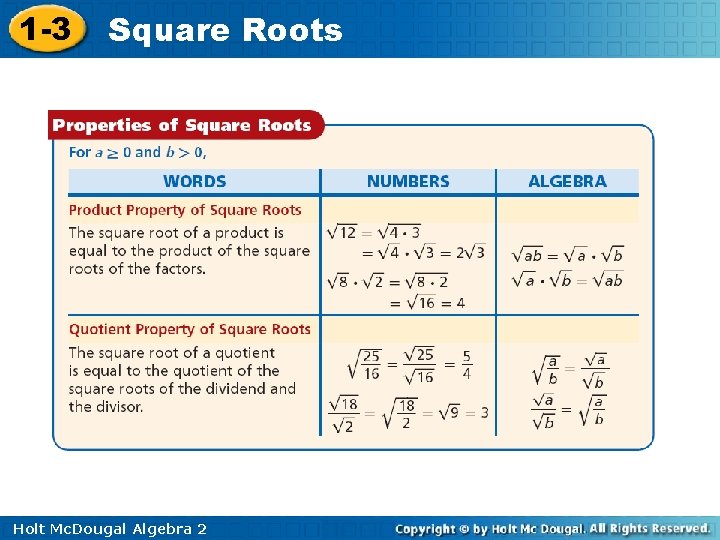
1 -3 Square Roots Square roots have special properties that help you simplify, multiply, and divide them. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Holt Mc. Dougal Algebra 2

1 -3 Square Roots Notice that these properties can be used to combine quantities under the radical symbol or separate them for the purpose of simplifying square-root expressions. A square-root expression is in simplest form when the radicand has no perfect-square factors (except 1) and there are no radicals in the denominator. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 2: Simplifying Square–Root Expressions Simplify each expression. A. Find a perfect square factor of 32. Product Property of Square Roots B. Quotient Property of Square Roots Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 2: Simplifying Square–Root Expressions Simplify each expression. C. Product Property of Square Roots D. Quotient Property of Square Roots Holt Mc. Dougal Algebra 2

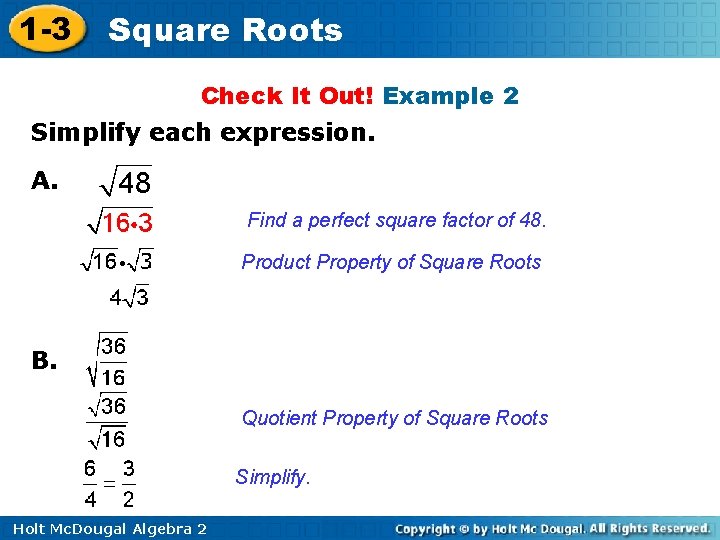
1 -3 Square Roots Check It Out! Example 2 Simplify each expression. A. Find a perfect square factor of 48. Product Property of Square Roots B. Quotient Property of Square Roots Simplify. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Check It Out! Example 2 Simplify each expression. C. Product Property of Square Roots D. Quotient Property of Square Roots Holt Mc. Dougal Algebra 2

1 -3 Square Roots If a fraction has a denominator that is a square root, you can simplify it by rationalizing the denominator. To do this, multiply both the numerator and denominator by a number that produces a perfect square under the radical sign in the denominator. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 3 A: Rationalizing the Denominator Simplify by rationalizing the denominator. Multiply by a form of 1. =2 Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 3 B: Rationalizing the Denominator Simplify the expression. Multiply by a form of 1. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Check It Out! Example 3 a Simplify by rationalizing the denominator. Multiply by a form of 1. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Check It Out! Example 3 b Simplify by rationalizing the denominator. Multiply by a form of 1. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Square roots that have the same radicand are called like radical terms. To add or subtract square roots, first simplify each radical term and then combine like radical terms by adding or subtracting their coefficients. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 4 A: Adding and Subtracting Square Roots Add. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Example 4 B: Adding and Subtracting Square Roots Subtract. Simplify radical terms. Combine like radical terms. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Check It Out! Example 4 a Add or subtract. Combine like radical terms. Holt Mc. Dougal Algebra 2

1 -3 Square Roots Check It Out! Example 4 b Add or subtract. Simplify radical terms. Combine like radical terms. Holt Mc. Dougal Algebra 2

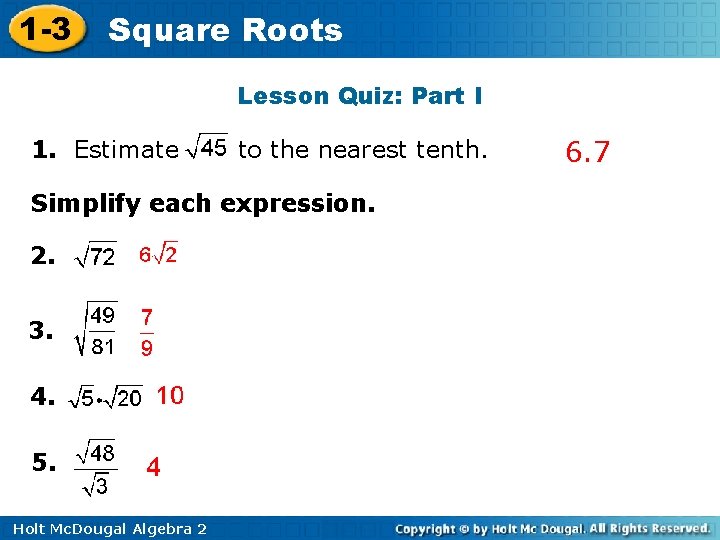
1 -3 Square Roots Lesson Quiz: Part I 1. Estimate to the nearest tenth. Simplify each expression. 2. 3. 4. 5. Holt Mc. Dougal Algebra 2 6. 7

1 -3 Square Roots Lesson Quiz: Part II Simplify by rationalizing each denominator. 6. 7. Add or subtract. 8. 9. Holt Mc. Dougal Algebra 2