1 3 Segments Rays and Distance A Terms

1 -3 Segments, Rays, and Distance • A) Terms: • 1) Line segment • - is part of a line that has end points. • - symbol: • AB or BA • Ex.

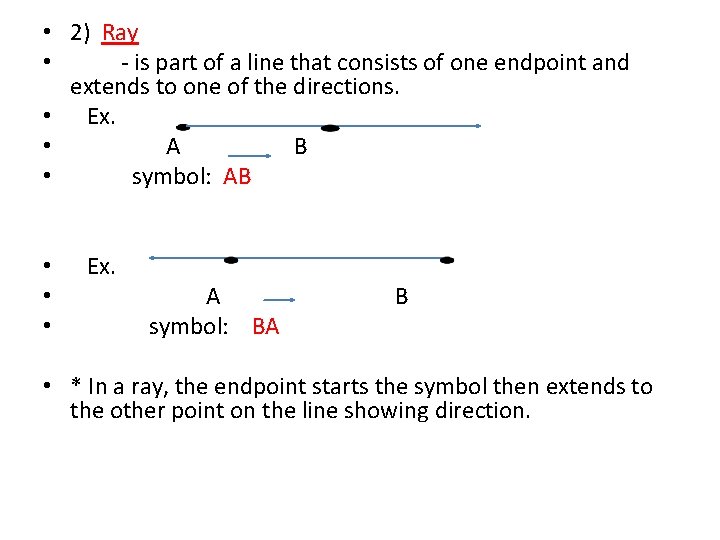
• 2) Ray • - is part of a line that consists of one endpoint and extends to one of the directions. • Ex. • A B • symbol: AB • • • Ex. A symbol: BA B • * In a ray, the endpoint starts the symbol then extends to the other point on the line showing direction.

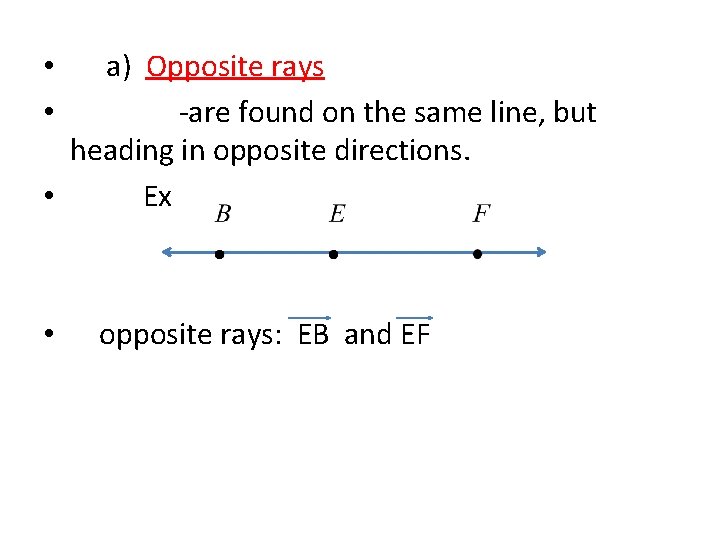
a) Opposite rays -are found on the same line, but heading in opposite directions. • Ex • • • opposite rays: EB and EF

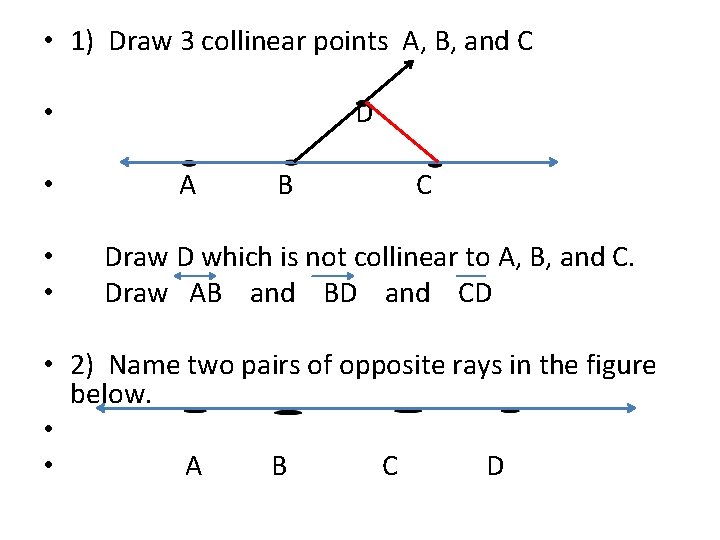
• 1) Draw 3 collinear points A, B, and C D • • A B C Draw D which is not collinear to A, B, and C. Draw AB and BD and CD • 2) Name two pairs of opposite rays in the figure below. • • A B C D

• 2) Draw four points J, K, L, and M, no three of which are collinear. Then sketch JK, KL, LM and MJ. [This is one diagram] • 3) Draw five points, P, Q, R, S, and T no three of which are collinear. Then sketch PQ, RS, QR, ST, and TP. [This is one diagram]

• 3) Postulates or Axioms • - statements that are accepted without proof. • 4) Congruent • - two objects that have the same size or shape. • symbol: • a) congruent segments – are segments that have equal lengths.

B) Postulate 1: Ruler Postulate • 1) each point on a line can be matched one to one with real numbers. • - the real numbers that correspond to a point are called coordinates. • 2) The distance between the points is the absolute value of the difference between the coordinates of the points. • 3) AB is also called the length of AB • Ex. A Points B • -3 Coordinates 1 • Distance of AB is | 1 - -3 | =

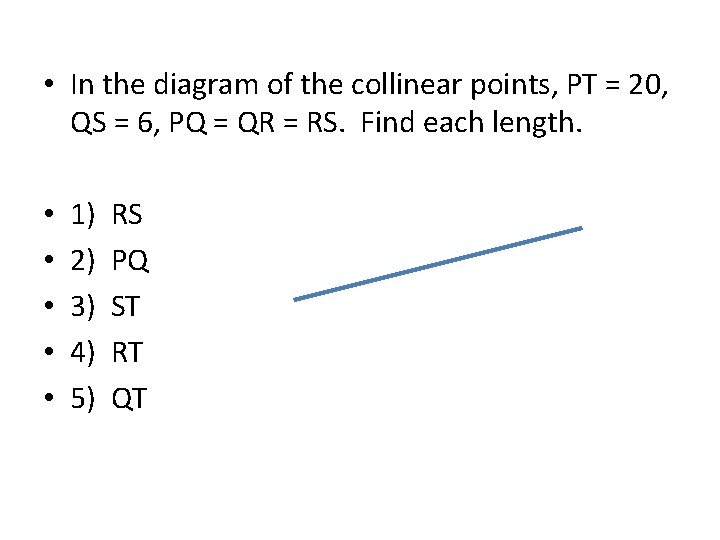
• In the diagram of the collinear points, PT = 20, QS = 6, PQ = QR = RS. Find each length. • • • 1) 2) 3) 4) 5) RS PQ ST RT QT

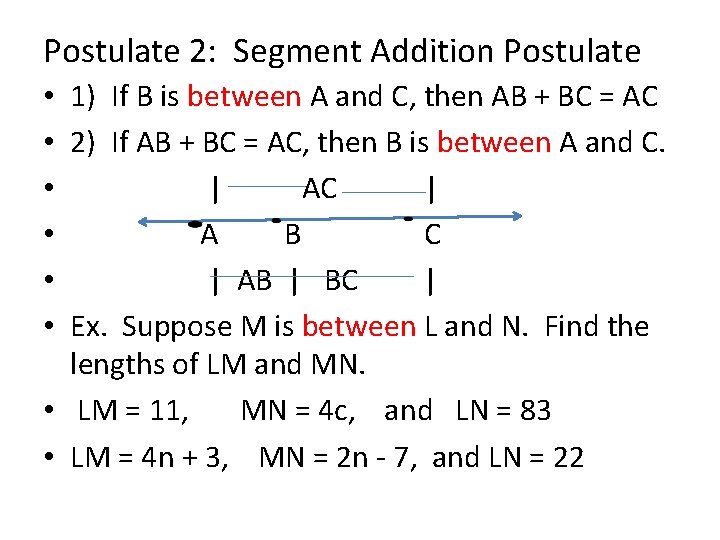
Postulate 2: Segment Addition Postulate • 1) If B is between A and C, then AB + BC = AC • 2) If AB + BC = AC, then B is between A and C. • | AC | • A B C • | AB | BC | • Ex. Suppose M is between L and N. Find the lengths of LM and MN. • LM = 11, MN = 4 c, and LN = 83 • LM = 4 n + 3, MN = 2 n - 7, and LN = 22

Student practice. • Suppose M is between L and N. Find the lengths LM and MN • 1) LM = 3 x + 8, MN = 2 x – 5, and LN = 23 • Suppose Y is between X and Z. Find the value of a. 2) XY = 3 a, YZ = 14, and XZ = 5 a - 4

• Suppose M is between L and N. Find LM and MN. • 3) LM = 7 y + 9 , MN = 3 y + 4, LN = 143 • Suppose Y is between X and Z. Find the value of d. • 4) XY = 11 d, YZ = 9 d – 2, and XZ = 5 d + 28

• 5) Midpoint of a segment • - is the point that divides the segment into 2 equal lengths. • ex. • • B is the midpoint of AC ex. 2 If B is the midpoint of AC and AB = x + 7 and BC = 3 x – 11. Find x

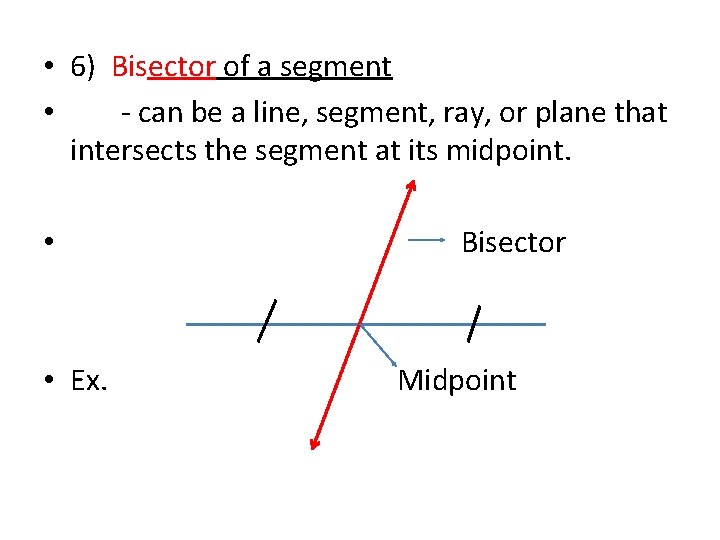
• 6) Bisector of a segment • - can be a line, segment, ray, or plane that intersects the segment at its midpoint. • • Ex. Bisector Midpoint

• Examples: • Q is the midpoint of PR, solve for y. • 1) PQ = 9 y – 2 QR = 14 + 5 y • 2) PQ = 3 x – 4 QR = 5 x – 26 • 3) PQ = 3 x – 4 QR = 5 x – 26 • 4) PQ = 7 x – 15 QR = 33