1 3 Relcik 1 Def rendezett pr Javtva

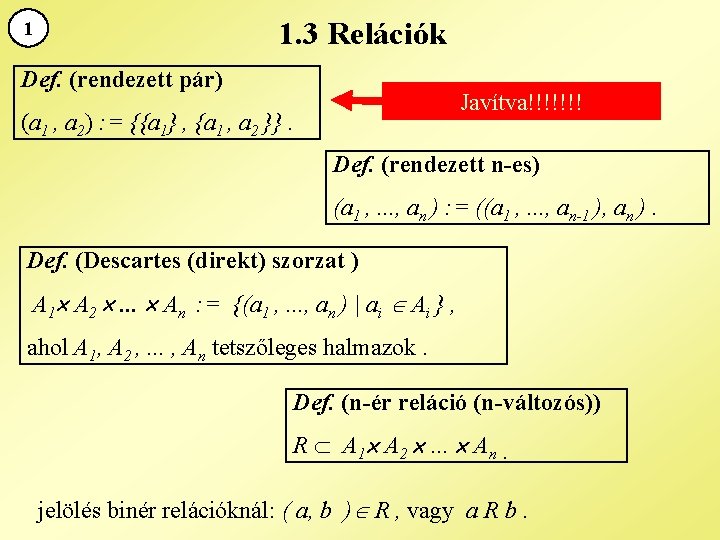
1. 3 Relációk 1 Def. (rendezett pár) Javítva!!!!!!! (a 1 , a 2) : = {{a 1} , {a 1 , a 2 }}. Def. (rendezett n-es) (a 1 , . . . , an ) : = ((a 1 , . . . , an-1 ), an ). Def. (Descartes (direkt) szorzat ) A 1 A 2 . . . An : = {(a 1 , . . . , an ) | ai Ai } , ahol A 1, A 2 , . . . , An tetszőleges halmazok. Def. (n-ér reláció (n-változós)) R A 1 A 2 . . . An . jelölés binér relációknál: ( a, b ) R , vagy a R b.

2 Def. (Homogén reláció) i, j { 1, 2, . . . , n } : Ai = Aj. Def. (R X Y reláció értelmezési tartománya ) dmn(R) : = { a X | b Y : (a, b) R }. Def. (R X Y reláció értékkészlete ) rng(R) : = { b Y | a X : (a, b) R }.

3 Def. Ha S R , akkor S az R leszűkítése, R az S kiterjesztése. Def. Az R reláció X halmazra való leszűkítése R|X : = { (a, b) R | a X }. Def. Az R X Y reláció inverze: R-1 = {(b, a) Y X | (a, b) R }. Észrevételek:

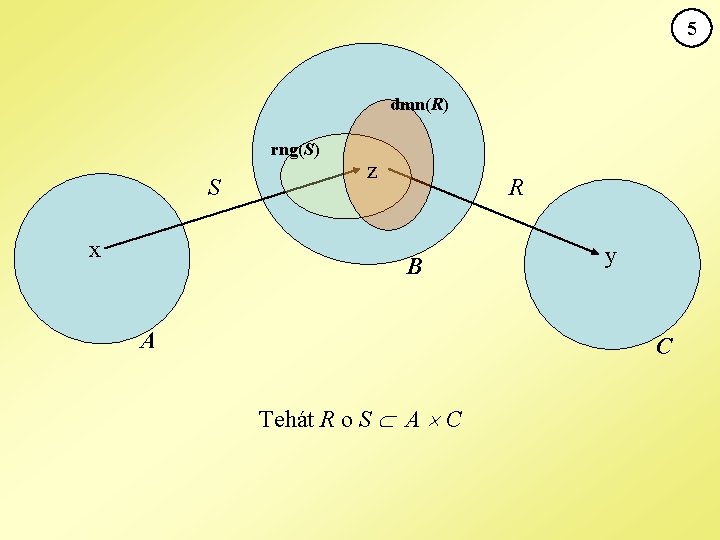
Def. Az A halmaz képe inverz (ős)képe Észrevétel: R(A) = A dmn(R) = . Def. Az S és R binér relációk kompozíciója Észrevétel: rng(S) dmn(R) = R o S = . 4

5 dmn(R) rng(S) S x z R B A y C Tehát R o S A C

Legyen A = { 1, 2 , 3, 4, 5}, B = { 6, 8 , 10, 12, 14}, 6 C = { 30, 36 , 42, 48, 54} , D = { 2, 3 }, S A B, ahol (a, b) S, ha b = 2 a , R B C, ahol (a, b) R, ha b = 3 a. Ekkor S(D) = { 6 }, S-1(S(D)) = { 3 }, S = { (3, 6) , (4, 8) , (5, 10) }, R = { (10, 30) , (12, 36) , (14, 42) }, dmn(S) = {3, 4, 5}, rng(S) = {6, 8, 10}, dmn(R) = {10, 12, 14}, rng(R) = {30, 36, 42}, R o S = { (5, 30) }.

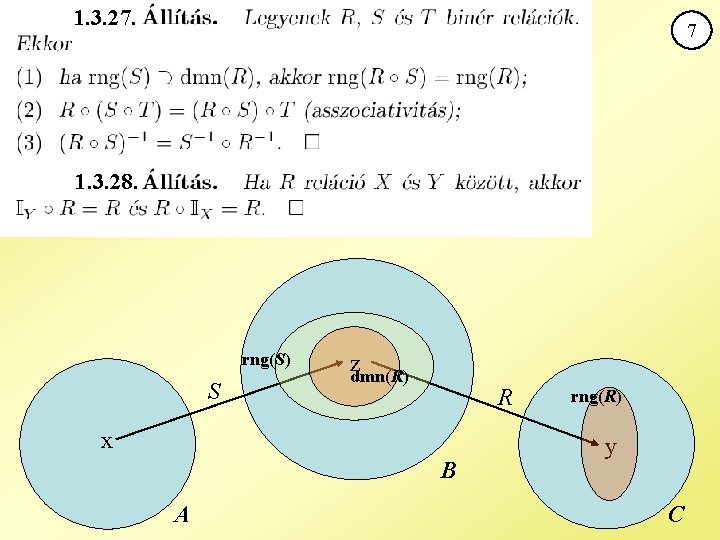
1. 3. 27. 7 1. 3. 28. rng(S) S zdmn(R) R x B A rng(R) y C

Homogén binér relációk tulajdonságai Legyen R A A alakú, ekkor R 1. reflexív : a A (a R a) 2. irreflexív : a A ¬(a R a) 3. szimmetrikus : a, b A (a R b b R a) 4. antiszimmetrikus : a, b A (a R b b R a b = a) 8

5. szigorúan antiszimmetrikus (asszimmetrikus): a, b A (a R b ¬(b R a)) 6. tranzitív : a, b, c A (a R b b R c a R c) 7. intranzitív : a, b, c A (a R b b R c ¬(a R c)) 8. trichotom : a, b A ( 1! áll fenn a R b, b R a, a=b közül ) 9. dichotom : a, b A (a R b b R a) 9

Def. ~ ekvivalenciareláció ha reflexív, tranzitív, szimmetrikus. Def. ( halmaz 10 osztályfelbontása ) A tetszőleges X halmazt osztályozzuk (osztályokra bontjuk), ha páronként diszjunkt, nemüres részhalmazainak úniójaként állítjuk elő. Az x X elem ekvivalencia osztálya:

1. 3. 38. . Biz. 1. , azaz tfh ~ ekvivalenciareláció X –n. reflexivitás x ~x osztályok nem üresek Mi újság két osztály metszetével ? tfh van nem üres: z ~x y~ tranz. +szimm. x ~ y , továbbá tranz. +szimm. Kaptuk: w x~ w y~ és ~ x y~ ~ x = y~ w y~ w x~. 11

Tehát a következő halmaz X –nek egy osztáyfelbontását adja: 2. , tfh X –nek osztályfelbontása: X 1 X 2 . . . Xn = X Legyen a relációnk: ρ : = { (a, b) X X | a, b Xi valamely 1 i n –re }. reflexív ? tranzitív ? szimmetrikus ? 12

Def. Az R X X reláció részbenrendezés ( ), ha 13 - reflexív, - tranzitív, - antiszimmetrikus, szigorú részbenrendezés ( < ), ha - irreflexív, - tranzitív. Def. Tetszőleges részbenrendezett halmaz esetén, ha bármely két elem relációban van, rendezésről (teljes rendezés) beszélünk. (X, ) részbenrendezett vagy rendezett struktúra, ha részbenrendezés vagy rendezés.

Tetszőleges X, a relációval részbenrendezett halmaz bármely Y részhalmaza részbenrendezett a Y Y relációval. Ha (Y, Y Y ) struktúra rendezés, akkor lánc. Tfh R X –beli reláció. Ha S X –beli reláció olyan, hogy x. Sy akkor áll fenn, ha x. Ry és x y, akkor S az R –nek megfelelő szigorú reláció. Tfh R X –beli reláció. Ha T X –beli reláció olyan, hogy x. Ty akkor áll fenn, ha x. Ry vagy x = y, akkor T az R –nek megfelelő gyenge reláció. < szigorú részbenrendzés irreflexív, tranzitív, szigorúan antiszimmetrikus. rendezés < trichotóm 14

Zárt intervallum: [x, y] = { z X | x z y }. Nyílt intervallum: (x, y) = { z X | x < z < y }. Jel: ] , x [ 15

Legyen (X, ) részbenrendezett struktúra, ekkor 16 m X az X minimális eleme, ha nem létezik olyan (m ) x X, amelyre m ≥ x , legkisebb eleme, ha minden x X – re m x. maximális és legnagyobb elem hasonlóan Észrevételek: legkisebb és legnagyobb elem legfeljebb egy van minimális és maximális elem több is lehet rendezett halmazban legkisebb és minimális egybeesik

Legyen B A (A részbenrendezett), ekkor a A a B alsó korlátja, ha minden x B – re a x , felső korlátja, ha minden x B – re x a. Észrevételek: lehet 0, vagy több korlát a korlát nem biztos, hogy B eleme ha egy korlát B –ben van, akkor 1! (legkisebb, vagy legnagyobb elem) 17

B infinuma (inf B), ha létezik, B legnagyobb alsó korlátja, pontos felső/alsó korlát, felső/alsó határ B supremuma (sup B), ha létezik, B legkisebbb felső korlátja. Tetszőleges részbenrendezett halmaz jólrendezett, ha bármely nemüres részhalmazának van legkisebb eleme. Észrevétel: jólrendezett 18

1. 4 Függvények Def. Az f reláció függvény, ha 19 (x, y) f (x, y’) f y = y’ Kapcsolódó jelölések, fogalmak: Az összes olyan függvény halmaza, amelynek értelmezési tartománya X – nek, értékkészlete pedig Y – nak része. rng(f) Y dmn(f) = X dmn(f) X parciális függvény

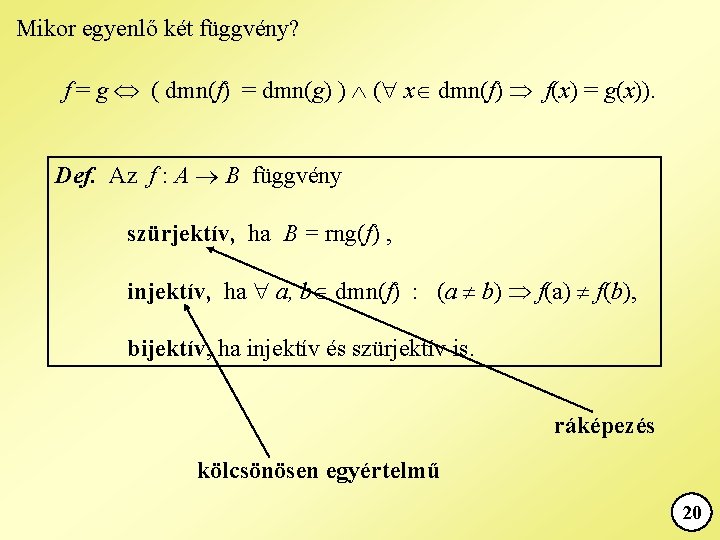
Mikor egyenlő két függvény? f = g ( dmn(f) = dmn(g) ) ( x dmn(f) f(x) = g(x)). Def. Az f : A B függvény szürjektív, ha B = rng(f) , injektív, ha a, b dmn(f) : (a b) f(a) f(b), bijektív, ha injektív és szürjektív is. ráképezés kölcsönösen egyértelmű 20

Észrevétel: injektív függvény inverze is függvény. 21 1. 4. 11. Ha adott egy X halmazon értelmezett ekvivalenciareláció, akkor az X elemeihez saját ekvivalenciaosztályukat rendelő leképezést (függvényt) kanonikus leképezésnek (függvénynek) nevezzük. Fordítva: ha f : X Y függvény, akkor ~ X X ekvivalenciareláció, ahol (x, y) ~ , ha f(x) = f(y)

Legyen (A, 1 ) , (B, 2 ) részbenrendezett struktúra. 22 Ekkor az f : A B függvény monoton növő, ha x, y dmn(f) : x 1 y f(x) 2 f(y) , szigorúan monoton növő, ha x, y dmn(f) : x <1 y f(x) <2 f(y). Csökkenő hasonlóan! Észrevételek: ha A és B rendezettek, akkor f szigorúan monoton f injektív monoton szigorúan monoton és f inverze is monoton.

Családok Legyen x függvény, dmn(x) = I és x(i) = y helyett írjunk x(i) = xi –t. Ekkor I indexhalmaz, rng(x) indexelt halmaz, x indexelt család. Ha rng(x) elemei halmazok, akkor halmazcsaládról beszélünk és egy Xi , i I halmazcsalád unióját így definiáljuk: I esetén halmazcsalád metszetét így definiáljuk: 23

1. 4. 22. 1. 4. 24. 24

25 Descartes – szorzat Def. Az Xi , i I halmazcsaládhoz tartozó kiválasztási függvénynek nevezzük azokat az alakú függvényeket, ahol i I -re xi Xi. Def. Az Xi , i I halmazcsalád Descartes – szorzata a hozzá tartozó összes kiválasztási függvény halmaza. Jel: vagy Észrevételek: ha i I : Xi = I= Def.

Példa (relációs adatbázis) 26 I = {személyi_szám, név, lakcím, végzettség} attribútumok (mezőnevek) Xszemélyi_szám ={11 jegyű decimális számok} olyan függvény, ahol i I -re xi Xi. xi a rekord i nevű mezője. Xi indexelt családhoz tartozó rekord Adattábla : Xi indexelt családhoz tartozó rekordok egy halmaza. Általánosítva: rekord: egy Xi indexelt családhoz tartozó kiválasztási függvény. Xi indexelt családhoz tartozó reláció: kiválasztási függvények egy halmaza.

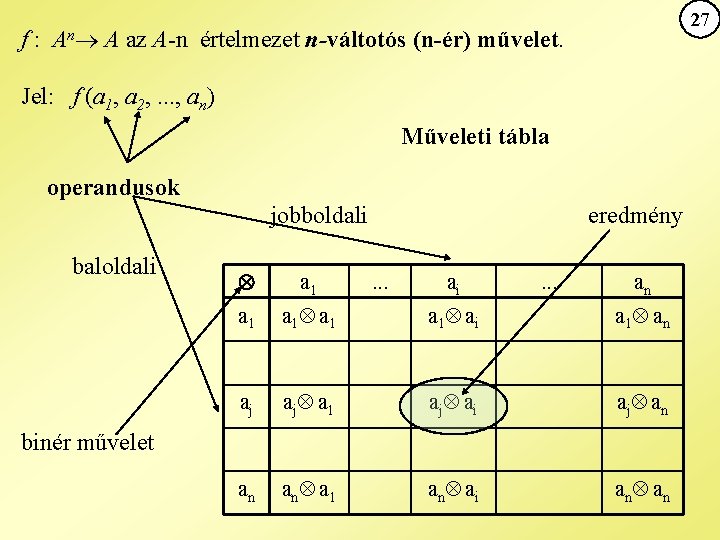
27 f : An A az A-n értelmezet n-váltotós (n-ér) művelet. Jel: f (a 1, a 2, . . . , an) Műveleti tábla operandusok jobboldali baloldali eredmény a 1 a 1 a 1 ai a 1 an aj a 1 a j a i a j a n an an a 1 an ai an an . . . ai . . . an binér művelet

Függvénytér (műveletek függvényekkel) 28 Ha X, Y tetszőleges halmaz és binér művelet Y-on, akkor legyen tehát binér művelet az X-et az Y-ba képező függvények halmazán, azaz : (X Y) Hasonlóan definiálható nullér és unér művelet is! Művelettató leképezés (homomorfizmus) Legyen · az A, a B halmazon értelmezett binér művelet. A : A B függvényt homomorfizmusnak nevezzük, ha művelettartó, vagyis minden a 1, a 2 A esetén (a 1 a 2) = (a 1) (a 2). injektív és művelettartó

Def. Legyen egy X halmazon értelmezett binér művelet és ~ egy ekvivalencia-reláció X-en. A művelet kompatibilis a ~ relációval illetve a megfelelő osztályozással, ha tetszőleges x, x’, y, y’ X-re x ~ x’ y ~ y’ x y ~ x’ y’. művelet ekvivalencia osztályokon művelettartó! kanonikus leképezés 29

Észrevétel ~ tulajdonságai miatt elég megkövetelni a kompatibilitáshoz, hogy: x y ~ x´ y és x y ~ x y´ legyen, mivel ekkor x´ y´ ~ x y´ és x´ y´ ~ x´ y tranzitivitás+szimmetria x y ~ x´ y´ reláció kompatibilitása osztályozással, hasonlóan 30