1 3 Measuring Angles Obj Measure angles with

1. 3: Measuring Angles Obj: Measure angles with a protractor. Identify and use the Angle Addition Postulate.

Using a Protractor to Measure Angles • Line arrow of protractor with vertex of angle • Place edge of protractor on one ray of angle • Determine which #’s to use (ray is on 0) • Find degree measure where other ray intersects the protractor

Ex: Measure the angles

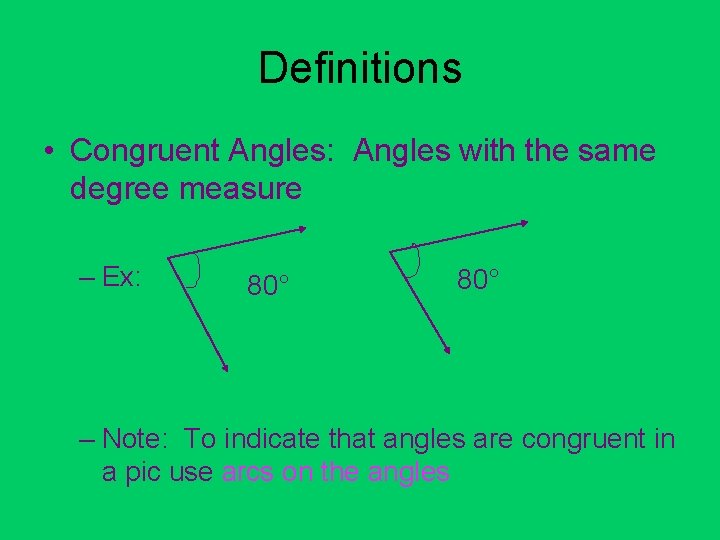
Definitions • Congruent Angles: Angles with the same degree measure – Ex: 80° – Note: To indicate that angles are congruent in a pic use arcs on the angles

Angle Congruence Postulate • If two angles have the same measure, then they are congruent. If two angles are congruent, then they have the same measure. – Ex: If <ABC = < DEF then m<ABC = m<DEF

Angle Addition Postulate • If point S is in the interior of < PQR, then m < PQS + m < SQR = m < PQR R Q S P

Special Angle Pairs • Complementary Angles: 2 angles whose measures have a sum of 90°. * Note: Each angle is called the Complement of the other 4 1 2 3

• Supplementary angles: 2 angles whose measures have a sum of 180˚ * Note: Each angle is called the Supplement of each other 5 6 7 8

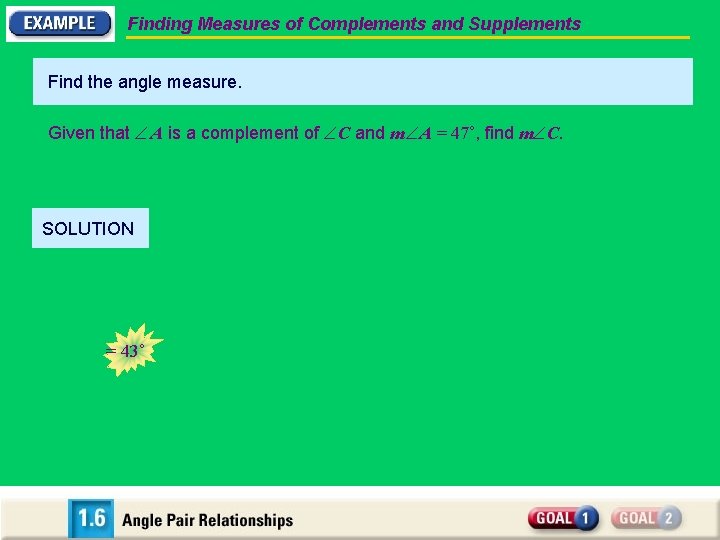
Finding Measures of Complements and Supplements Find the angle measure. Given that A is a complement of C and m A = 47˚, find m C. SOLUTION = 43˚

Finding Measures of Complements and Supplements Find the angle measure. Given that A is a complement of C and m A = 47˚, find m C. Given that P is a supplement of R and m R = 36˚, find m P. SOLUTION = 144˚

Finding the Measure of a Complement W and Z are complementary. The measure of Z is 5 times the measure of W. Find m W SOLUTION you know that m W = 15˚.

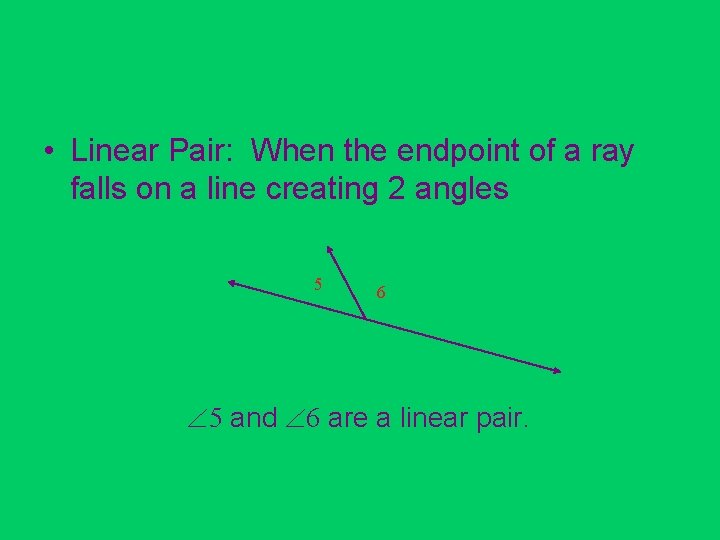
• Linear Pair: When the endpoint of a ray falls on a line creating 2 angles 5 6 5 and 6 are a linear pair.

• Linear Pair Property: If 2 angles form a linear pair then they are supplementary.

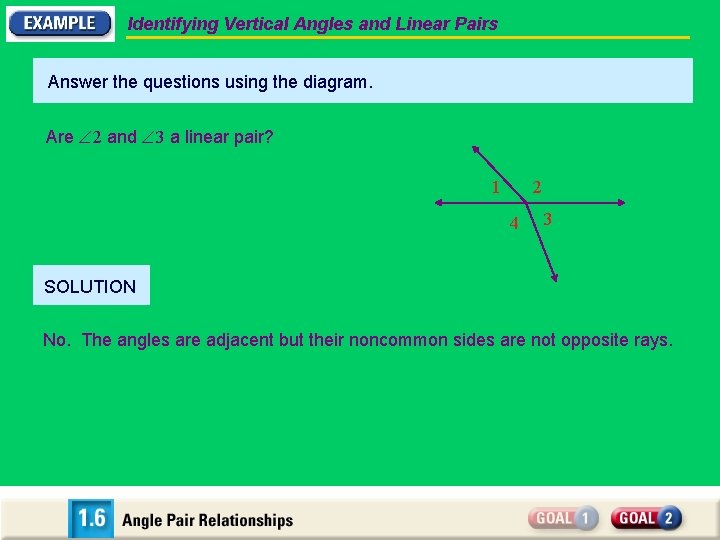
Identifying Vertical Angles and Linear Pairs Answer the questions using the diagram. Are 2 and 3 a linear pair? 1 2 4 3 SOLUTION No. The angles are adjacent but their noncommon sides are not opposite rays.

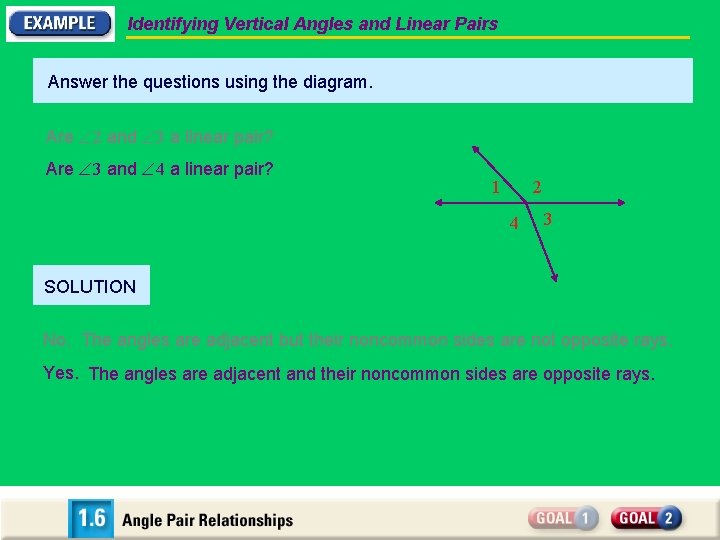
Identifying Vertical Angles and Linear Pairs Answer the questions using the diagram. Are 2 and 3 a linear pair? Are 3 and 4 a linear pair? 1 2 4 3 SOLUTION No. The angles are adjacent but their noncommon sides are not opposite rays. Yes. The angles are adjacent and their noncommon sides are opposite rays.

Types of Angles • Acute: 0 -90 degrees • Right: 90 degrees • Obtuse: 90 -180 degrees • Straight: 180 degrees

Practice: In the picture name the following: • • • 1) Congruent angles 2) Comp. angles 3) Supp angles 4) Linear pair 5) Obtuse angle 6) acute angle