1 3 Describing Quantitative Data with Numbers Section

1. 3 Describing Quantitative Data with Numbers

Section 1. 3 After this section, you should be able to: • Measure center with mean and median • Measure spread with standard deviation and interquartile range • Identify outliers • Construct a boxplot using the five number summary • Calculate numerical summaries with technology

How long do people spend travelling to work? The answer depends on where they live. Below are the travel times in minutes for 15 workers in North Carolina chosen by random by the Census Bureau: 30 20 10 40 25 20 10 60 15 40 5 30 12 10 10 What is the mean? 0 5 1 000025 2 005 Mean = 22. 5 3 00 4 00 What is the median? Median = 20 5 6 0

Measuring Center: The Mean •

Measuring Center: The Median • The median M is the midpoint of the distribution To find the median of the distribution: 1. Arrange all observations from smallest to largest 2. If the number of observations is n odd, the median M is the center observation in the ordered list. 3. If the number of observations is n even, the median M is the average of the two center observations in the ordered list.

Comparing the Mean and the Median The mean and median measure center in different ways, and both are useful Mean: “average” value Median: “typical” value Relationship between mean and median • The mean and median of a roughly symmetric distribution are close together • If the distribution is exactly symmetric, the mean and median are exactly the same. • In a skewed distribution, the mean is usually farther out in the long tail than is the median.

Example: 10 15 Mean = 31. 25 Use the data below to calculate the mean and median of commuting time (in minutes) of 20 randomly selected New York workers. 0 5 30 20 5 85 25 15 40 65 20 15 10 60 15 60 30 40 20 45 1 00555 5 2 0005 3 00 Median = 22. 5 4 005 5 6 005 7 8 5

Measuring Spread: Range and Interquartile Range (IQR) Range • Measures variability • Single number that represents distance between maximum and the minimum values • Max – Min = range • “The data values range from 5 mins to 85 mins. ” – NO, do no write this! • Instead, “The data values vary from 5 mins to 85 mins and the range is 80 mins. ”
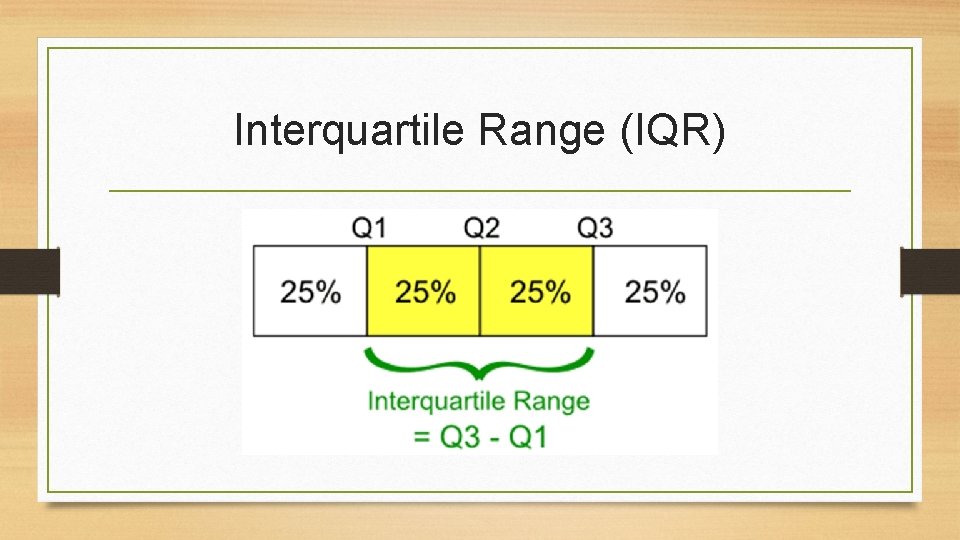
Interquartile Range (IQR)

Interquartile Range (IQR) •

Identifying Outliers Interquartile range is a rule of thumb for identifying outliers. 1. 5 x IQR Rule for Outliers Call an observation an outlier if it falls more than 1. 5 x IQR above third quartile or below the first quartile.
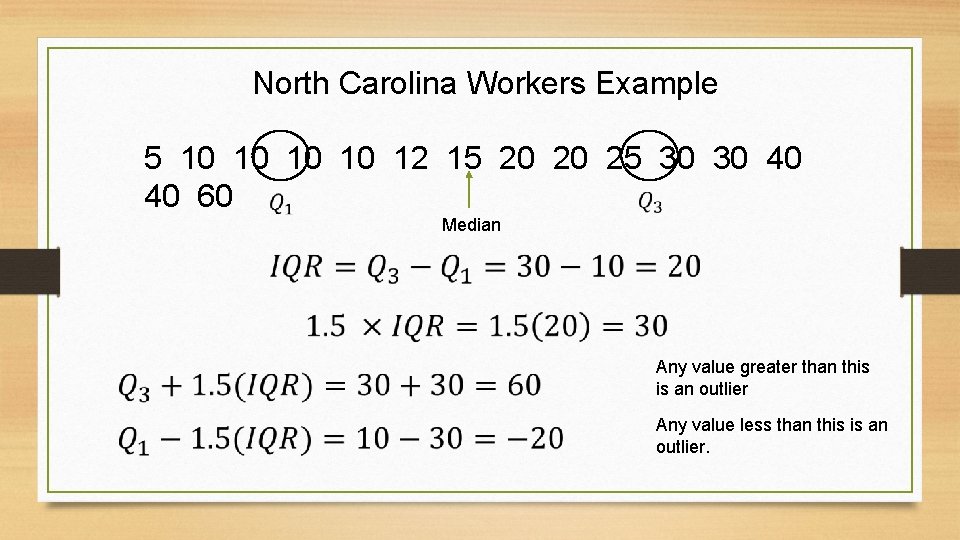
North Carolina Workers Example 5 10 10 12 15 20 20 25 30 30 40 40 60 Median Any value greater than this is an outlier Any value less than this is an outlier.
- Slides: 12