1 2 Points Lines and Planes Goal to






- Slides: 20

1. 2 Points, Lines, and Planes Goal, to use undefined terms and definitions.

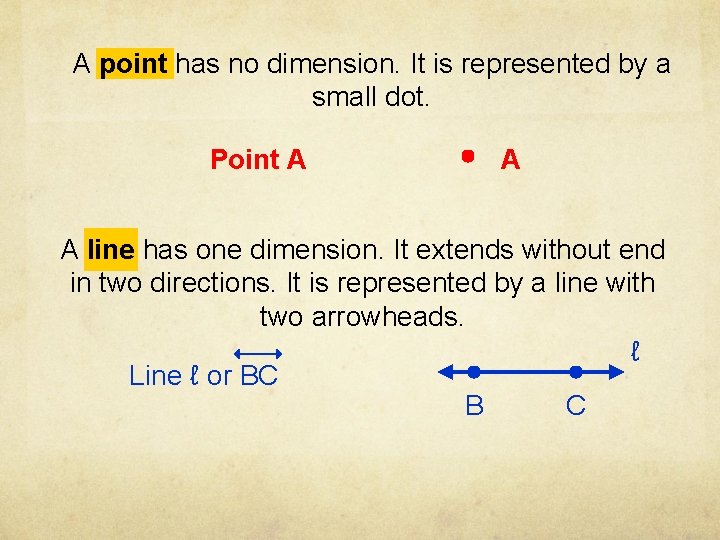
A point has no dimension. It is represented by a small dot. Point A A A line has one dimension. It extends without end in two directions. It is represented by a line with two arrowheads. ℓ Line ℓ or BC B C

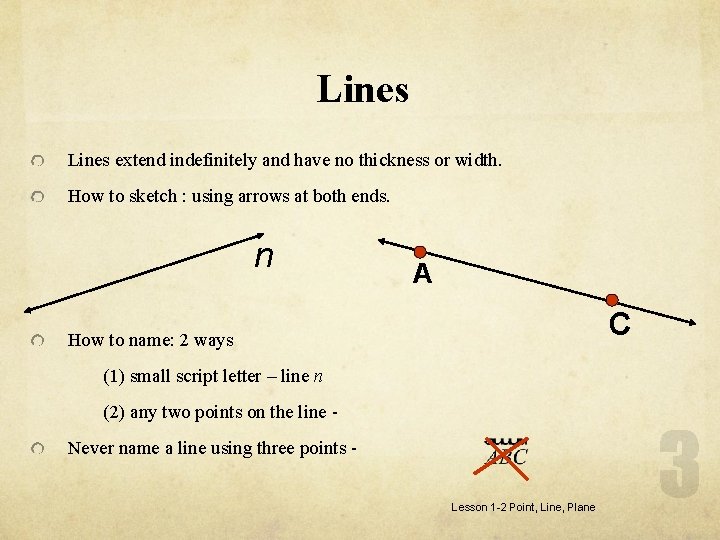
Lines extend indefinitely and have no thickness or width. How to sketch : using arrows at both ends. n A C How to name: 2 ways (1) small script letter – line n (2) any two points on the line Never name a line using three points Lesson 1 -2 Point, Line, Plane

Points do not have actual size. How to Sketch: A Using dots How to label: B Use capital letters Never name two points with the same letter (in the same sketch). Lesson 1 -2 Point, Line, Plane C A

Collinear Points Collinear points are points that lie on the same line. (The line does not have to be visible. ) A B Collinear Non collinear A B C Lesson 1 -2 Point, Line, Plane C

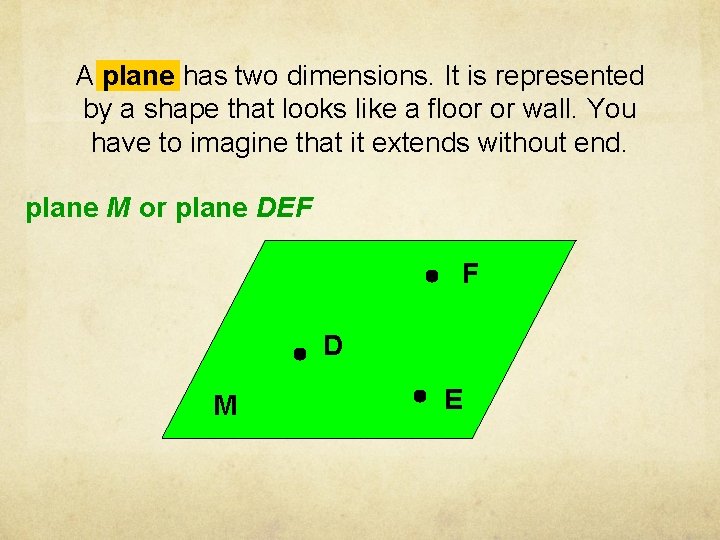
A plane has two dimensions. It is represented by a shape that looks like a floor or wall. You have to imagine that it extends without end. plane M or plane DEF F D M E

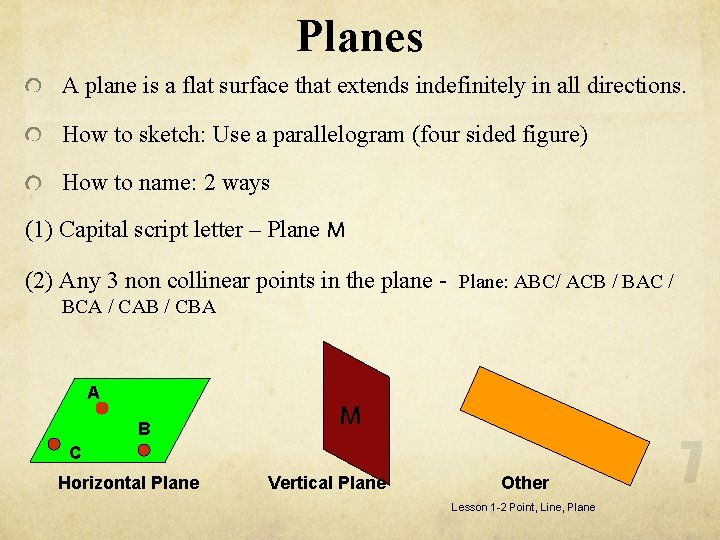
Planes A plane is a flat surface that extends indefinitely in all directions. How to sketch: Use a parallelogram (four sided figure) How to name: 2 ways (1) Capital script letter – Plane M (2) Any 3 non collinear points in the plane - Plane: ABC/ ACB / BAC / BCA / CAB / CBA A B M C Horizontal Plane Vertical Plane Other Lesson 1 -2 Point, Line, Plane

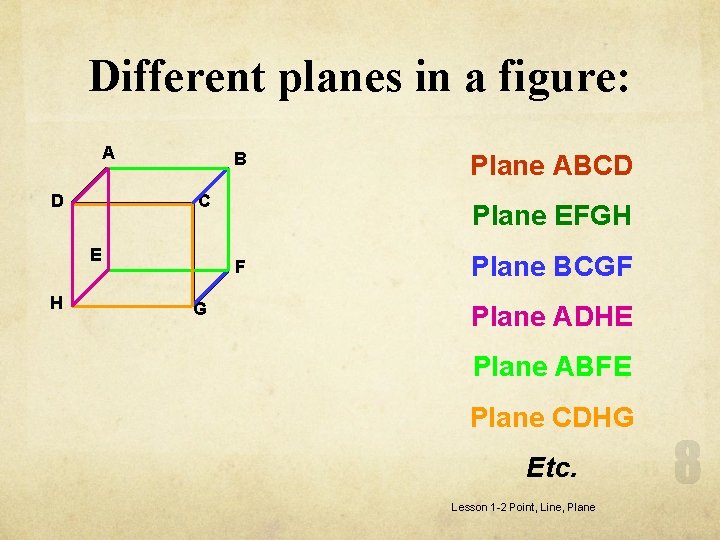
Different planes in a figure: A D B C E H Plane EFGH F G Plane ABCD Plane BCGF Plane ADHE Plane ABFE Plane CDHG Etc. Lesson 1 -2 Point, Line, Plane

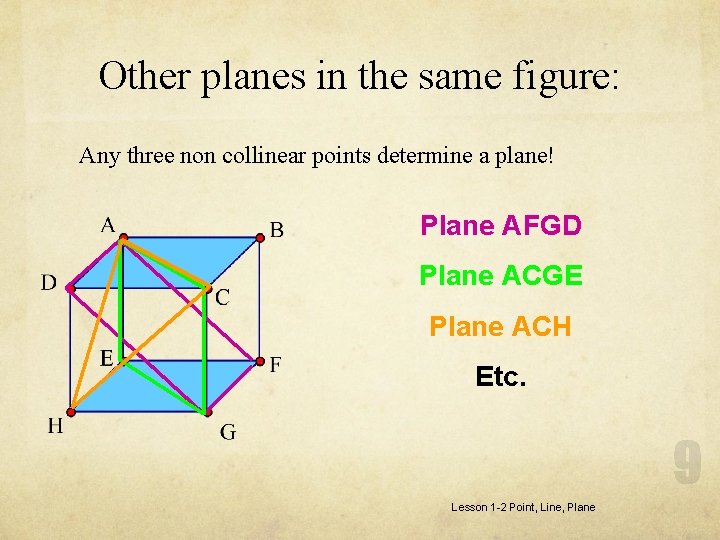
Other planes in the same figure: Any three non collinear points determine a plane! Plane AFGD Plane ACGE Plane ACH Etc. Lesson 1 -2 Point, Line, Plane

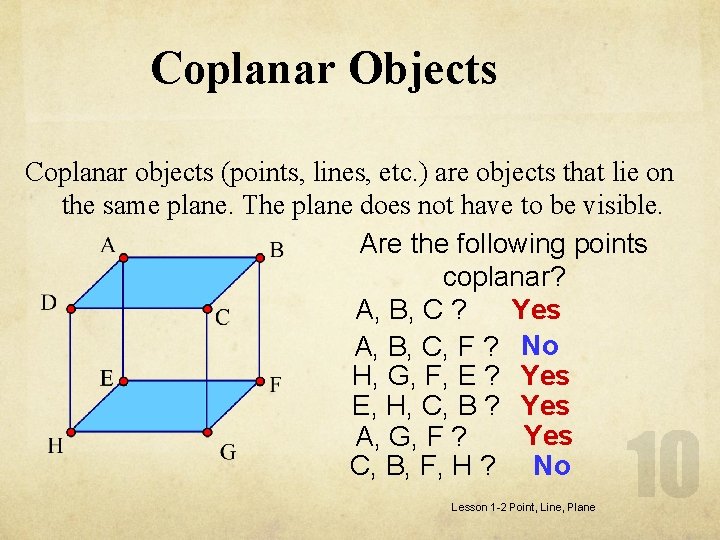
Coplanar Objects Coplanar objects (points, lines, etc. ) are objects that lie on the same plane. The plane does not have to be visible. Are the following points coplanar? A, B, C ? Yes A, B, C, F ? No H, G, F, E ? Yes E, H, C, B ? Yes A, G, F ? C, B, F, H ? No Lesson 1 -2 Point, Line, Plane

Postulates are statements that are accepted without further justification or proof. Postulates (write this down) Postulate, Two points determine a line. Through any two points there is exactly one line. Postulate, Three points determine a plane. Through any three points not on a line there is exactly one plane.

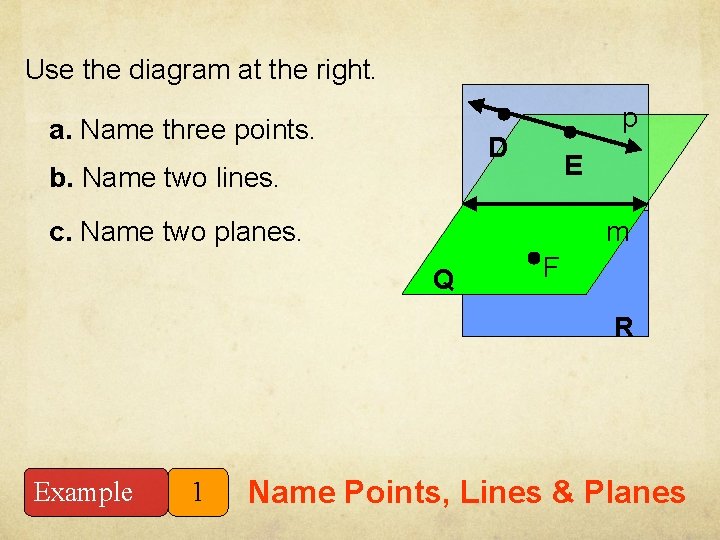
Use the diagram at the right. a. Name three points. p D b. Name two lines. E c. Name two planes. m Q F R Example 1 Name Points, Lines & Planes

Collinear points are points that lie on the same line Coplanar points are points that lie on the same plane. Coplanar lines are lines that lie on the same plane.

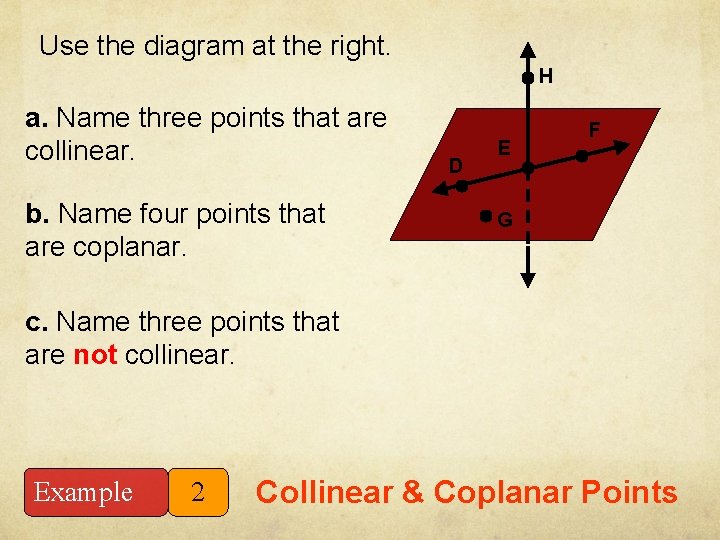
Use the diagram at the right. H a. Name three points that are collinear. b. Name four points that are coplanar. D E F G c. Name three points that are not collinear. Example 2 Collinear & Coplanar Points

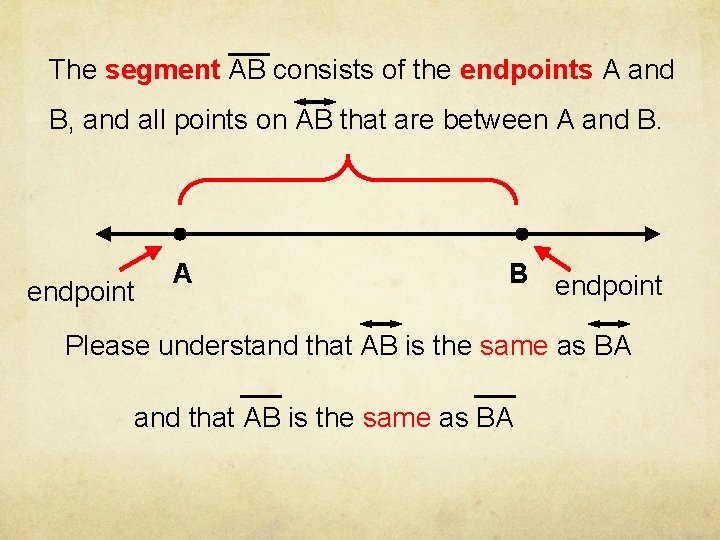
The segment AB consists of the endpoints A and B, and all points on AB that are between A and B. endpoint A B endpoint Please understand that AB is the same as BA

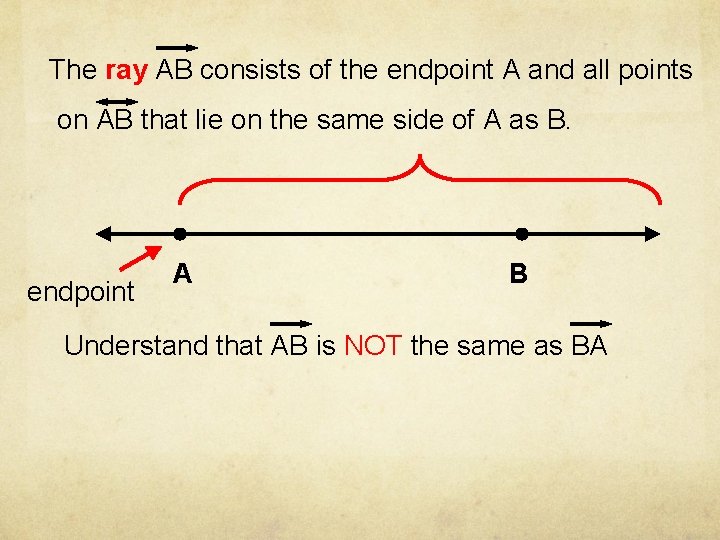
The ray AB consists of the endpoint A and all points on AB that lie on the same side of A as B. endpoint A B Understand that AB is NOT the same as BA

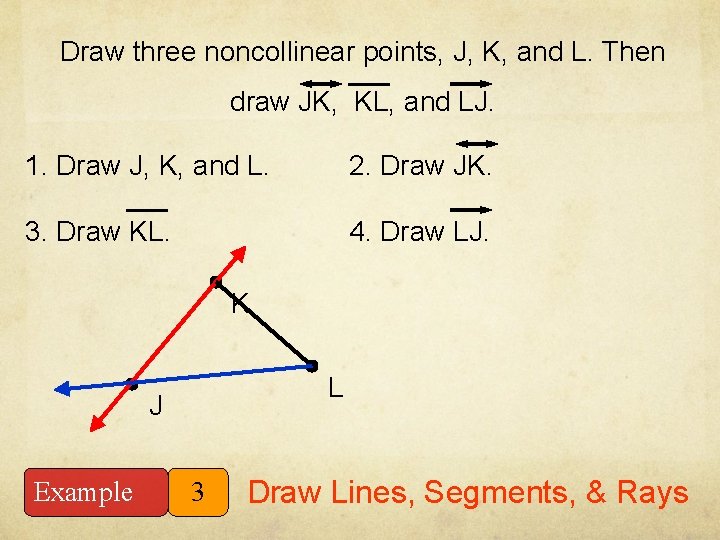
Draw three noncollinear points, J, K, and L. Then draw JK, KL, and LJ. 1. Draw J, K, and L. 2. Draw JK. 3. Draw KL. 4. Draw LJ. K L J Example 3 Draw Lines, Segments, & Rays

Intersection of Figures The intersection of two figures is the set of points that are common in both figures. The intersection of two lines is a point. m Line m and line n intersect at P point P. n Continued……. Lesson 1 -1 Point, Line, Plane

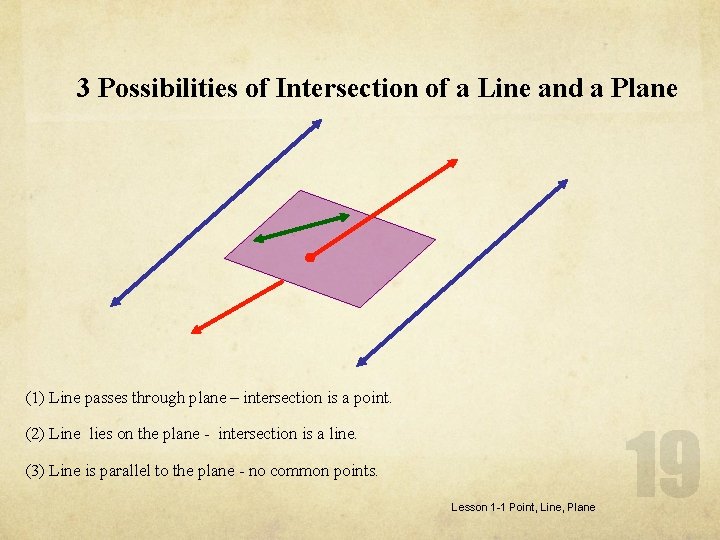
3 Possibilities of Intersection of a Line and a Plane (1) Line passes through plane – intersection is a point. (2) Line lies on the plane - intersection is a line. (3) Line is parallel to the plane - no common points. Lesson 1 -1 Point, Line, Plane

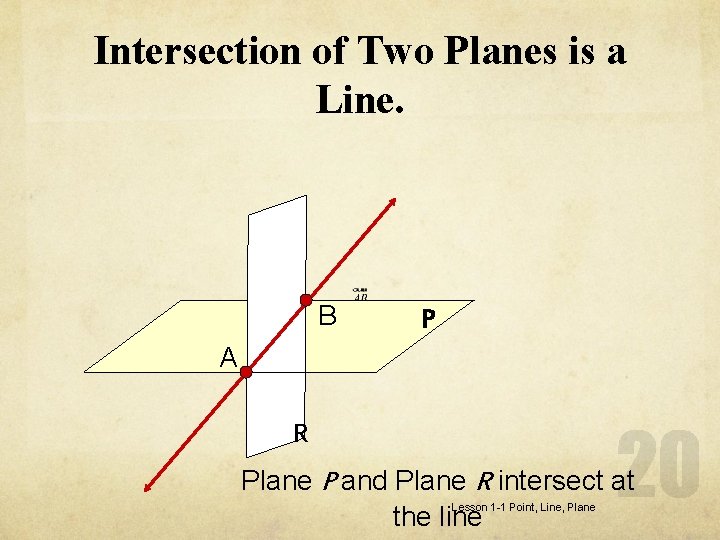
Intersection of Two Planes is a Line. B P A R Plane P and Plane R intersect at the line Lesson 1 -1 Point, Line, Plane