1 2 Measuring Segments Objectives Use length and

1 -2 Measuring Segments Objectives Use length and midpoint of a segment. Apply distance and midpoint formula.

Vocabulary coordinate midpoint distance bisect length segment bisector congruent segments

A point corresponds to one and only one number (or coordinate) on a number line.

Distance (length): the absolute value of the difference of the coordinates. A B a b AB = |a – b| or |b - a|
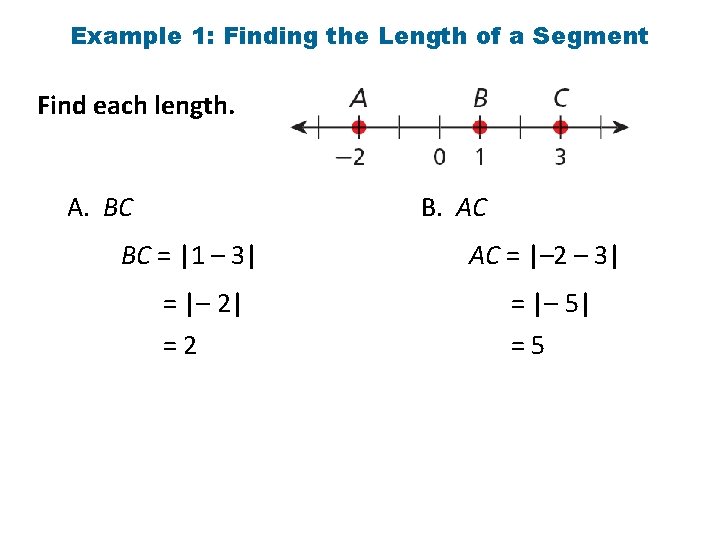
Example 1: Finding the Length of a Segment Find each length. A. BC B. AC BC = |1 – 3| AC = |– 2 – 3| = |– 2| = |– 5| =2 =5

Point B is between two points A and C if and only if all three points are collinear and AB + BC = AC. A


bisect: cut in half; divide into 2 congruent parts. midpoint: the point that bisects, or divides, the segment into two congruent segments

4 x + 6 = 7 x - 9 +9 +9 4 x + 15 = 7 x -4 x 15 = 3 x 3 3 5=x

It’s Mr. Jam-is-on Time!

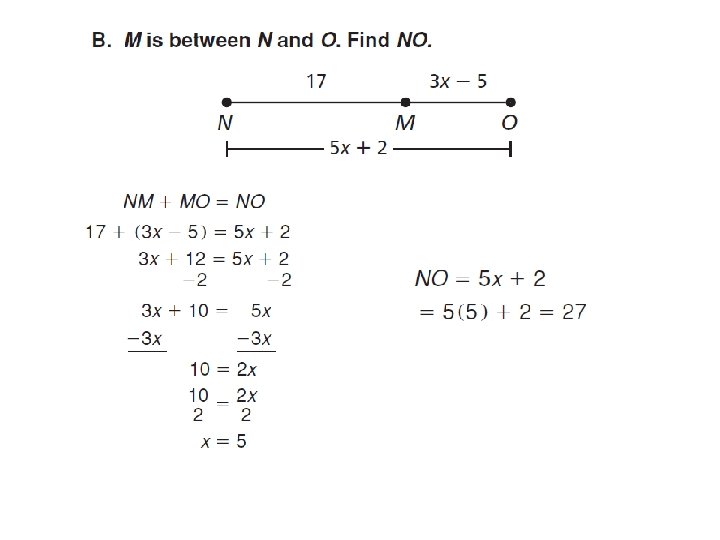
Recap! 1. M is between N and O. MO = 15, and MN = 7. 6. Find NO. 2. S is the midpoint of TV, TS = 4 x – 7, and SV = 5 x – 15. Find TS, SV, and TV. 3. LH bisects GK at M. GM = 2 x + 6, and GK = 24. Find x.

1. M is between N and O. MO = 15, and MN = 7. 6. Find NO.

2. S is the midpoint of TV, TS = 4 x – 7, and SV = 5 x – 15. Find TS, SV, and TV.
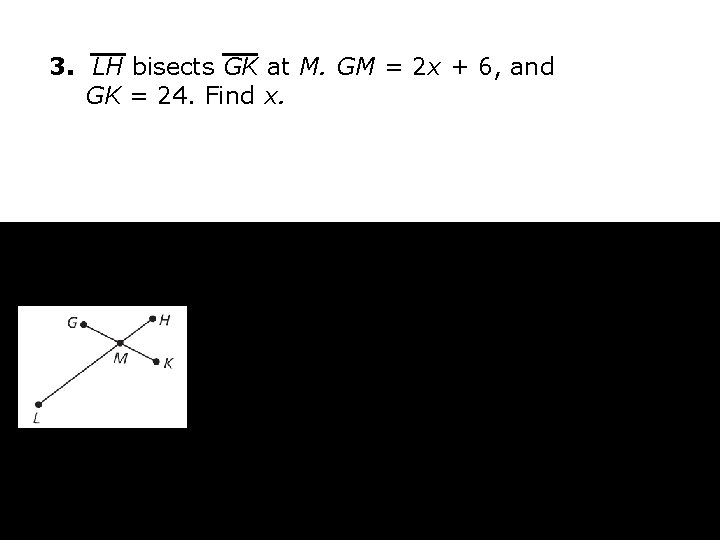
3. LH bisects GK at M. GM = 2 x + 6, and GK = 24. Find x.

1 -6 Midpoint and Distance in the Coordinate Plane

Vocabulary • Coordinate plane: a plane that is divided into four regions by a horizontal line called the x-axis and a vertical line called the y-axis II I x-axis III IV The location, or coordinates, of a point is given by an ordered pair (x, y).

Midpoint Formula The midpoint M of a AB with endpoints A(x 1, y 1) and B(x 2, y 2) is found by

Example Find the midpoint of GH with endpoints G(1, 2) and H(7, 6).

Example M(3, -1) is the midpoint of CD and C has coordinates (1, 4). Find the coordinates of D.

Distance Formula The distance d between points A(x 1, y 1) and B(x 2, y 2) is

Example Use the Distance Formula to find the distance between A(1, 2) and B(7, 6).
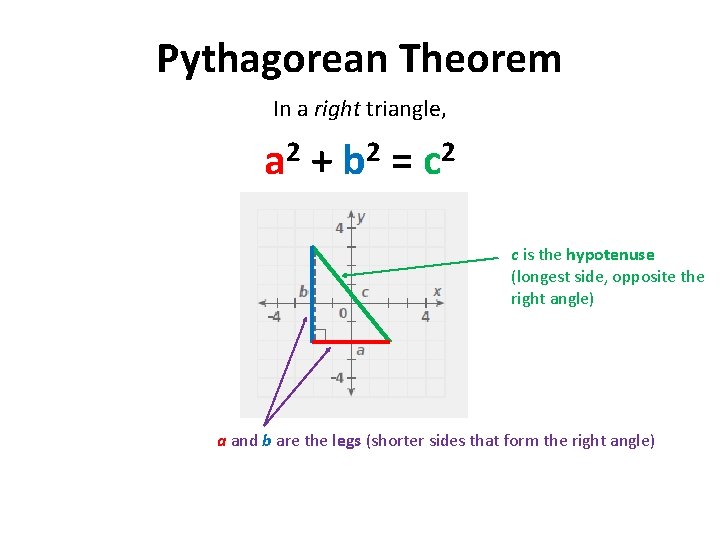
Pythagorean Theorem In a right triangle, a 2 + b 2 = c 2 c is the hypotenuse (longest side, opposite the right angle) a and b are the legs (shorter sides that form the right angle)
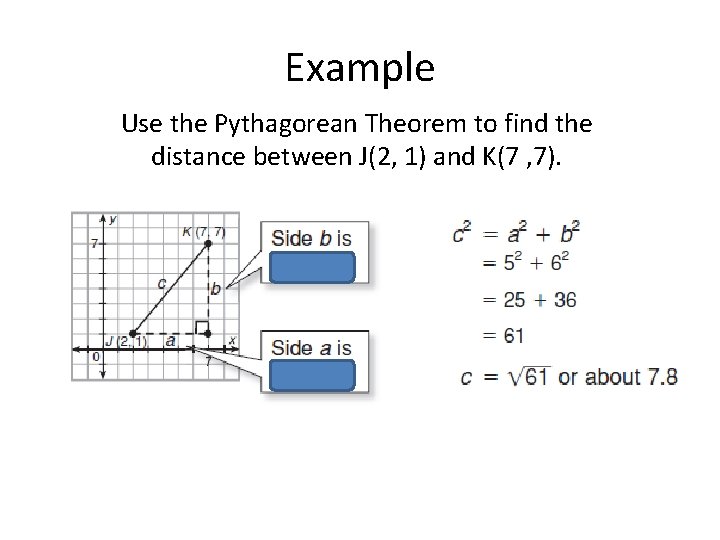
Example Use the Pythagorean Theorem to find the distance between J(2, 1) and K(7 , 7).
- Slides: 24