1 2 Measuring Length Objectives Define length congruence

1. 2 Measuring Length Objectives: • Define length & congruence • Identify and use the segment addition postulate Warm-Up: Place 10 dishes along the 4 edges of a table so that each edge had the same amount of dishes.

Vocabulary: Number Line: A line whose points correspond with the set of real numbers. -5 -4 -3 -2 -1 0 1 2 3 4 5

Vocabulary: Coordinate of a Point: The real number represented by a point on the number line. A -5 -4 -3 -2 -1 0 1 2 3 4 5 Note: 2 is the coordinate of point A

Vocabulary: Length of AB: The measure of AB is |a-b| or |b-a|. A -5 -4 -3 -2 B -1 0 1 2 3 4 5 AB = | a – b | = | -3 – 2| = | -5 | = 5 or AB = | b – a | = | 2 – -3| = | 2 + 3 | = | 5 | = 5

Vocabulary: Congruence: The relationship between figures have the same shape and same size. (congruent segments are segments that match exactly) ~ =

Vocabulary: Segment Congruence Postulate: If two segments have the same length then they are congruent. Also, if two segments are congruent they have the same length.
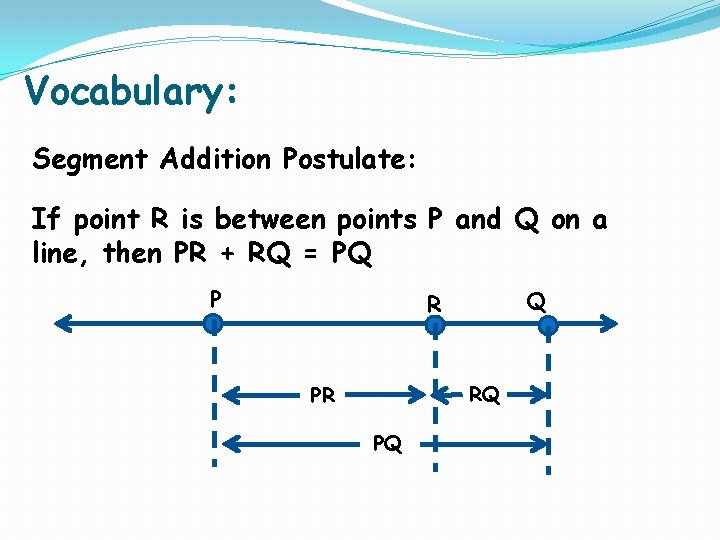
Vocabulary: Segment Addition Postulate: If point R is between points P and Q on a line, then PR + RQ = PQ P Q R RQ PR PQ
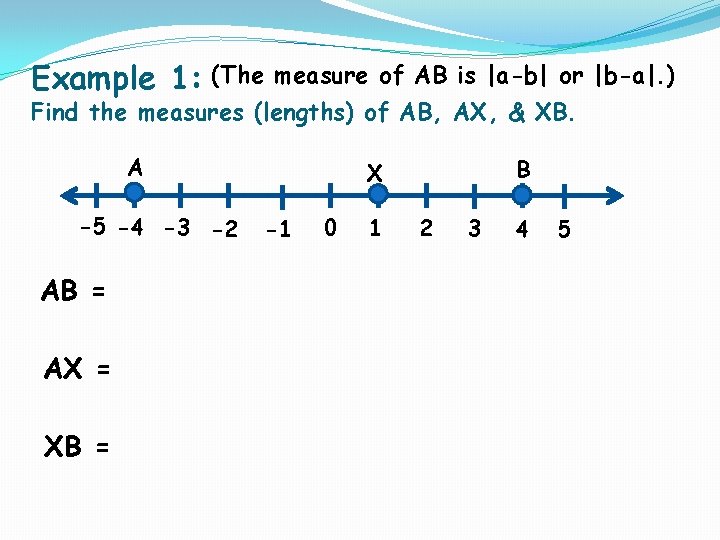
Example 1: (The measure of AB is |a-b| or |b-a|. ) Find the measures (lengths) of AB, AX, & XB. A -5 -4 -3 -2 AB = AX = XB = B X -1 0 1 2 3 4 5

Collins Writing Type 1: The length of a segment must be a positive number. Explain why the order of the coordinates does not matter when calculating length. _________________________________________ 3 lines ~ 2 minutes
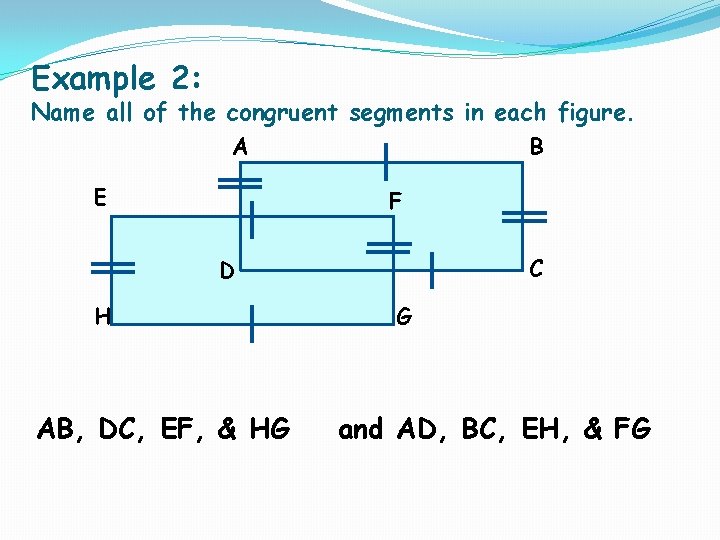
Example 2: Name all of the congruent segments in each figure. A E B F C D H AB, DC, EF, & HG G and AD, BC, EH, & FG
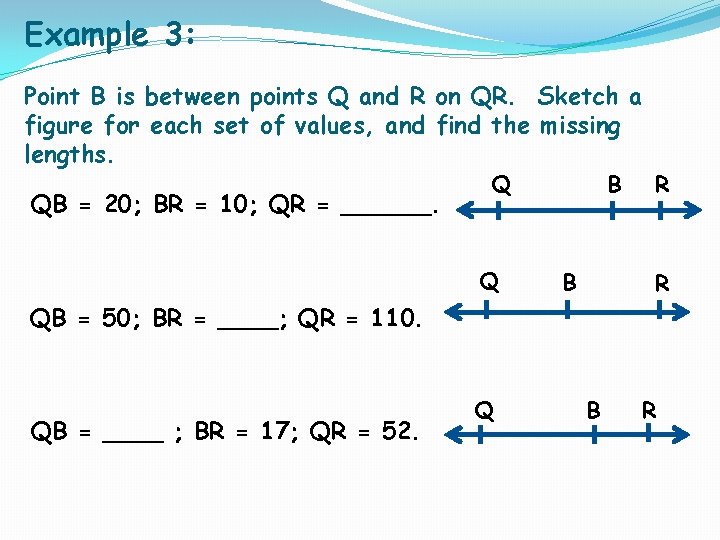
Example 3: Point B is between points Q and R on QR. Sketch a figure for each set of values, and find the missing lengths. QB = 20; BR = 10; QR = ______. Q Q B B R R QB = 50; BR = ____; QR = 110. QB = ____ ; BR = 17; QR = 52. Q B R
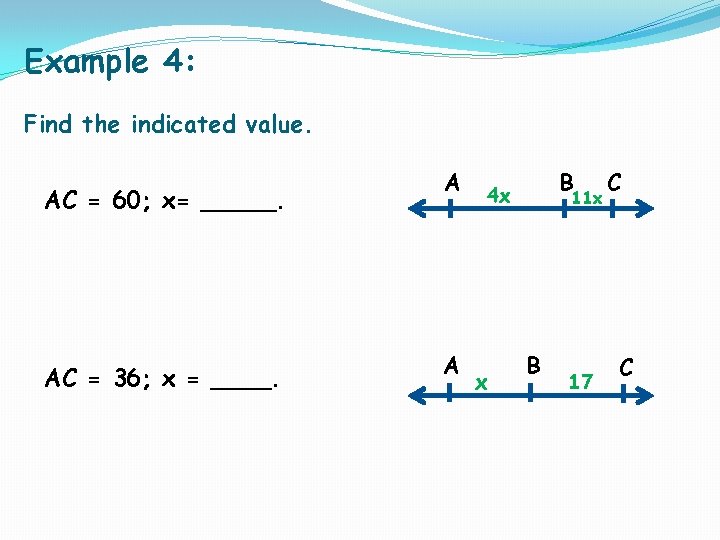
Example 4: Find the indicated value. AC = 60; x= _____. AC = 36; x = ____. A A B 4 x x 11 x B 17 C C
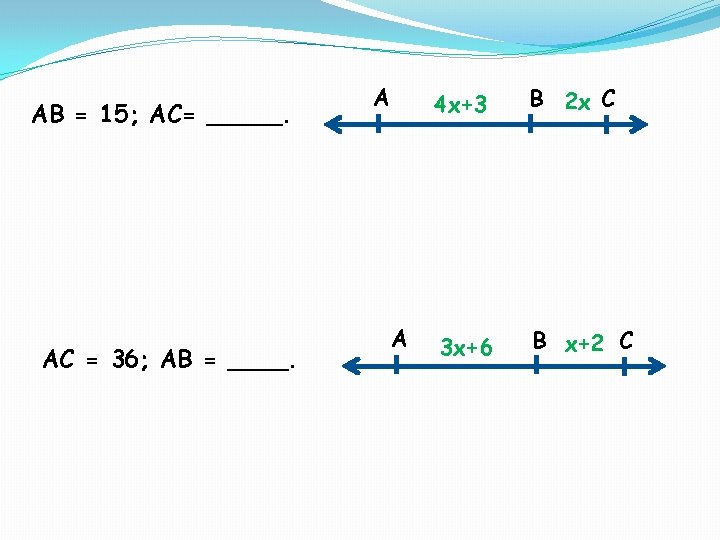
AB = 15; AC= _____. AC = 36; AB = ____. A A 4 x+3 B 2 x C 3 x+6 B x+2 C

Homework: Page 22 Numbers 11 -25
- Slides: 14