1 2 Line Segments and Distance LESSON 1

























- Slides: 33

1– 2 Line Segments and Distance LESSON 1– 2 Line Segments and Distance

1– 2 Line Segments and Distance Five-Minute Check (over Lesson 1– 1) TEKS Then/Now New Vocabulary Key Concept: Betweenness of Points Example 1: Finding Measurements by Adding or Subtracting Example 2: Write and Solve Equations to Find Measurements Key Concept: Congruent Segments Key Concept: Distance Formula (on Number Line) Example 3: Find Distance on a Number Line Key Concept: Distance Formula (in Coordinate Plane) Example 4: Find Distance on a Coordinate Plane Example 5: Find Distance

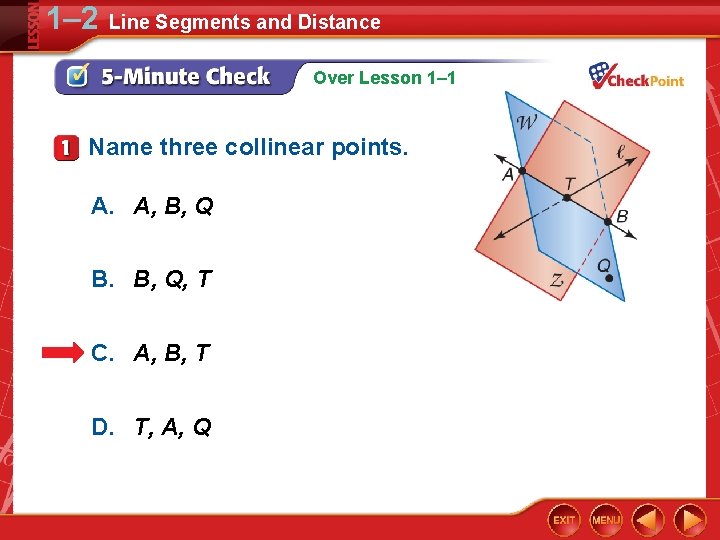
1– 2 Line Segments and Distance Over Lesson 1– 1 Name three collinear points. A. A, B, Q B. B, Q, T C. A, B, T D. T, A, Q

1– 2 Line Segments and Distance Over Lesson 1– 1 What is another name for AB? A. AA B. AT C. BQ D. QB

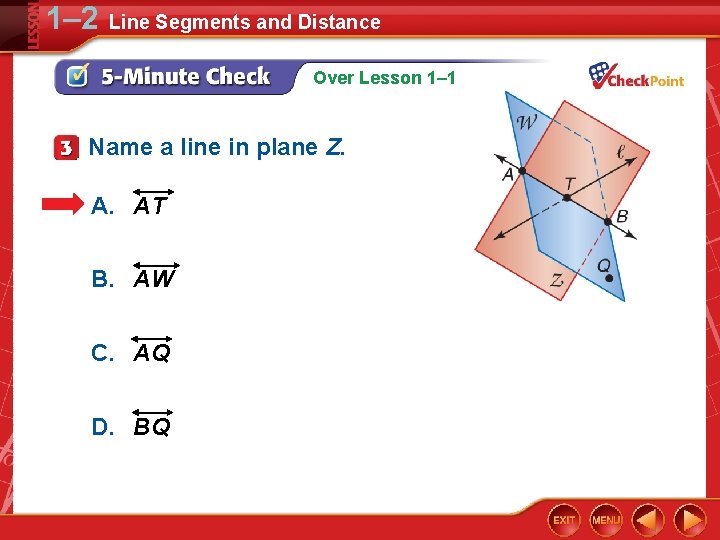
1– 2 Line Segments and Distance Over Lesson 1– 1 Name a line in plane Z. A. AT B. AW C. AQ D. BQ

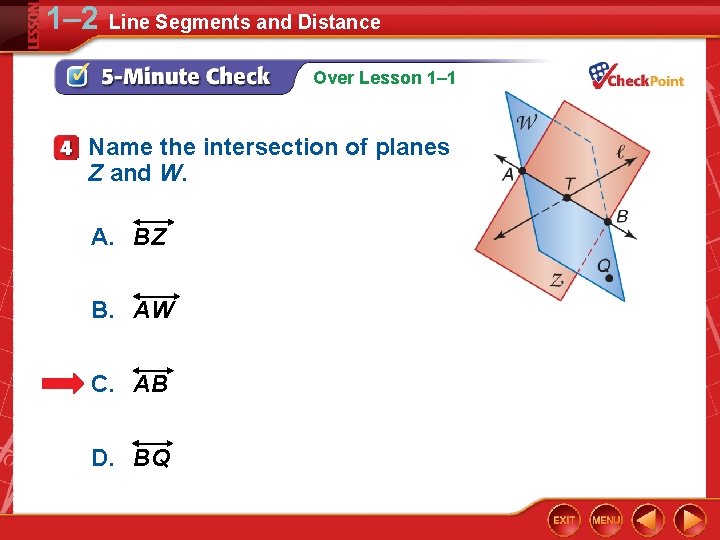
1– 2 Line Segments and Distance Over Lesson 1– 1 Name the intersection of planes Z and W. A. BZ B. AW C. AB D. BQ

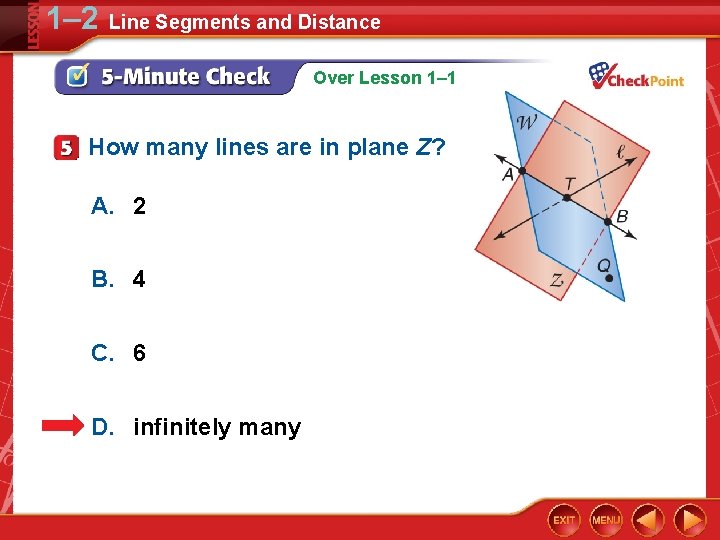
1– 2 Line Segments and Distance Over Lesson 1– 1 How many lines are in plane Z? A. 2 B. 4 C. 6 D. infinitely many

1– 2 Line Segments and Distance Over Lesson 1– 1 Which of the following statements is always false? A. The intersection of a line and a plane is a point. B. There is only one plane perpendicular to a given plane. C. Collinear points are also coplanar. D. A plane contains an infinite number of points.

1– 2 Line Segments and Distance Targeted TEKS G. 2(B) Derive and use the distance, slope, and midpoint formulas to verify geometric relationships, including congruence of segments and parallelism or perpendicularity of pairs of lines. G. 5(B) Construct congruent segments, congruent angles, a segment bisector, an angle bisector, perpendicular lines, the perpendicular bisector of a line segment, and a line parallel to a given line through a point not on a line using a compass and straightedge. Also addresses G. 5(C). Mathematical Processes G. 1(E), Also addresses G. 1(B)

1– 2 Line Segments and Distance You identified points, lines, and planes. • Calculate with measures. • Find the distance between two points.

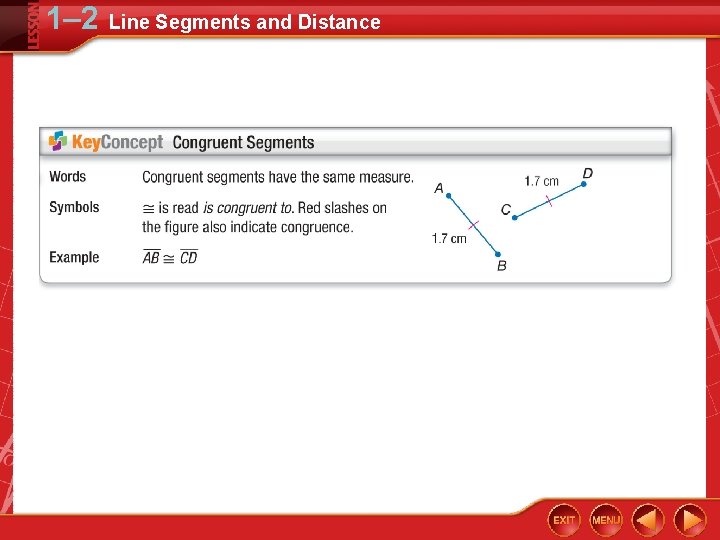
1– 2 Line Segments and Distance • line segment • distance • betweenness of points • irrational number • between • congruent • rigid transformation • congruent segments • construction

1– 2 Line Segments and Distance

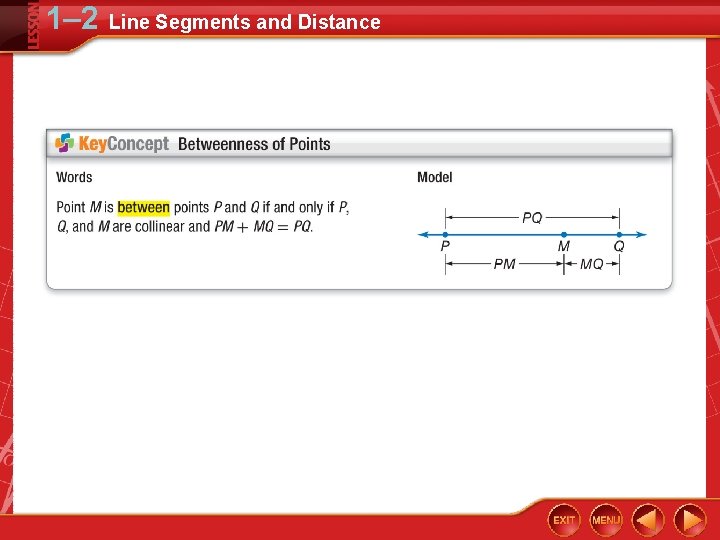
1– 2 Line Segments and Distance Find Measurements by Adding or Subtracting Find XZ. Assume that the figure is not drawn to scale. ___ XZ is the measure of XZ. Point Y is between X and Z. XZ can be found by adding XY and YZ.

1– 2 Line Segments and Distance Find Measurements by Adding or Subtracting Add.

1– 2 Line Segments and Distance Find BD. Assume that the figure is not drawn to scale. 50. 4 mm A. 16. 8 mm B. 57. 4 mm 16. 8 mm B C. 67. 2 mm D. 84 mm C D

1– 2 Line Segments and Distance Write and Solve Equations to Find Measurements ALGEBRA Find the value of x and ST if T is between S and U, ST = 7 x, SU = 45, and TU = 5 x – 3. Draw a figure to represent this situation. ST + TU = SU 7 x + 5 x – 3 = 45 7 x + 5 x – 3 + 3 = 45 + 3 12 x = 48 Betweenness of points Substitute known values. Add 3 to each side. Simplify.

1– 2 Line Segments and Distance Write and Solve Equations to Find Measurements x =4 Simplify. Now find ST. ST = 7 x Given = 7(4) x=4 = 28 Multiply. Answer: x = 4, ST = 28

1– 2 Line Segments and Distance ALGEBRA Find the value of n and WX if W is between X and Y, WX = 6 n – 10, XY = 17, and WY = 3 n. A. n = 3; WX = 8 B. n = 3; WX = 9 C. n = 9; WX = 27 D. n = 9; WX = 44

1– 2 Line Segments and Distance

1– 2 Line Segments and Distance

1– 2 Line Segments and Distance Find Distance on a Number Line Use the number line to find QR. The coordinates of Q and R are – 6 and – 3. QR = | – 6 – (– 3) | = | – 3 | or 3 Answer: 3 Distance Formula Simplify.

1– 2 Line Segments and Distance Use the number line to find AX. A. 2 B. 8 C. – 2 D. – 8

1– 2 Line Segments and Distance

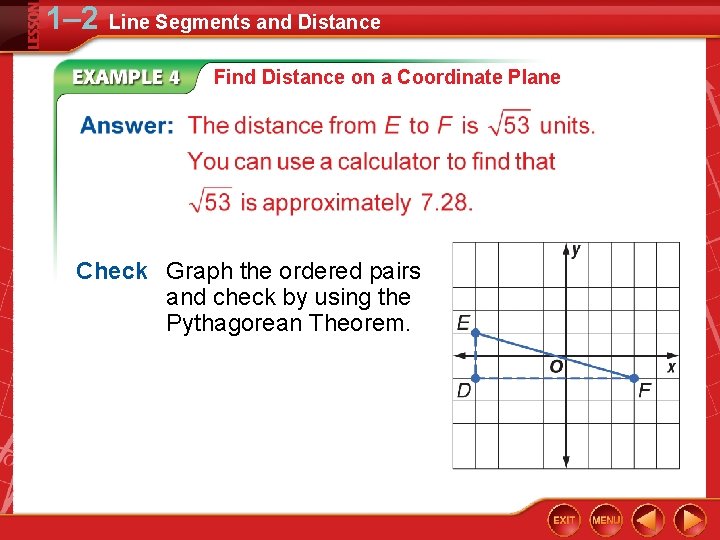
1– 2 Line Segments and Distance Find Distance on a Coordinate Plane Find the distance between E(– 4, 1) and F(3, – 1). (x 1, y 1) = (– 4, 1) and (x 2, y 2) = (3, – 1)

1– 2 Line Segments and Distance Find Distance on a Coordinate Plane Check Graph the ordered pairs and check by using the Pythagorean Theorem.

1– 2 Line Segments and Distance Find Distance on a Coordinate Plane .

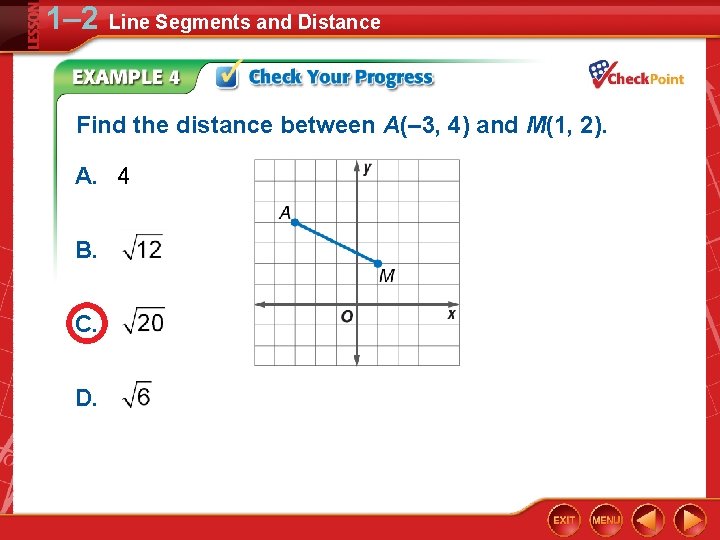
1– 2 Line Segments and Distance Find the distance between A(– 3, 4) and M(1, 2). A. 4 B. C. D.

1– 2 Line Segments and Distance Find Distance Josh is standing at the 30 -yard line, 15 yards from the sideline, when he throws the football. Johnny catches it on the other team’s 20 -yard line, 5 yards from the same sideline. How far did Josh throw the ball? Analyze. First draw a diagram to represent the situation.

1– 2 Line Segments and Distance Find Distance Formulate. Use the Distance Formula where (x 1, y 1) = (30, 15) and (x 2, y 2) = (80, 5). Determine

1– 2 Line Segments and Distance Find Distance Josh threw the football approximately 51 yards. Justify Josh is 50 yards from the other team’s 20 yard line where Johnny is located, and he is 10 yards farther from the sideline than Johnny. Use the Pythagorean Theorem to justify the answer. c 2 c 2 c = a 2 + b 2 = 502 + 102 = 2600 ≈ 51

1– 2 Line Segments and Distance Find Distance Evaluate. You are able to determine Josh’s and Johnny’s locations in terms of points on a coordinate plane and can use the Distance Formula to calculate the distance between them. The calculated distance seems reasonable.

1– 2 Line Segments and Distance FOOTBALL Ben is standing at the 40 -yard line, 20 yards from the sideline, when he throws the football. Eric catches it on the other team’s 30 -yard line 10 yards from the same sideline. How far did Ben throw the ball? A. 45. 9 yards B. 50. 7 yards C. 41. 2 yards D. 31. 6 yards

1– 2 Line Segments and Distance LESSON 1– 2 Line Segments and Distance