1 2 Introduction to Relations and Functions Two







- Slides: 11

1. 2 Introduction to Relations and Functions Two Types of Notation: 1. Set Builder Notation {x | x > – 2} is read “The set of all x such that x is greater than – 2” 2. Interval Notation (– 2, ) represents the set of all numbers greater than – 2 • Note that a left parenthesis “(“ indicates that – 2 is not included. A parenthesis is always next to the infinity symbol . Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -1

1. 2 Type of Interval Copyright © 2011 Pearson Education, Inc. Interval Notation Example of Set-Builder Notation Corresponding Interval Notation Corresponding Graph Slide 1. 2 -2

1. 2 Relation, Domain, and Range A relation is a set of ordered pairs. If we denote the ordered pairs of a relation by (x, y), - the set of all x-values is called the domain, and the set of all y-values is called the range. Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -3

1. 2 Example of a Relation Let F be a relation where F = {(1, 2), (– 2, 5), (3, – 1 )}. The Domain = {1, – 2, 3} and the Range = {2, 5, – 1}. The graph of F looks like the following: Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -4

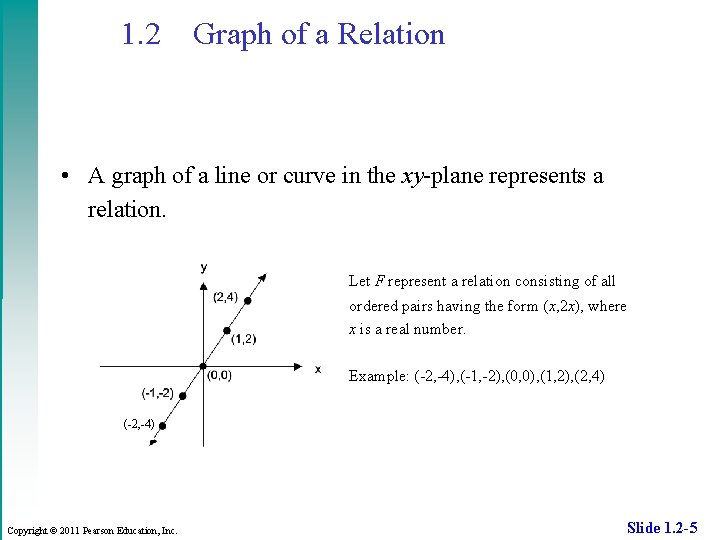
1. 2 Graph of a Relation • A graph of a line or curve in the xy-plane represents a relation. Let F represent a relation consisting of all ordered pairs having the form (x, 2 x), where x is a real number. Example: (-2, -4), (-1, -2), (0, 0), (1, 2), (2, 4) (-2, -4) Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -5

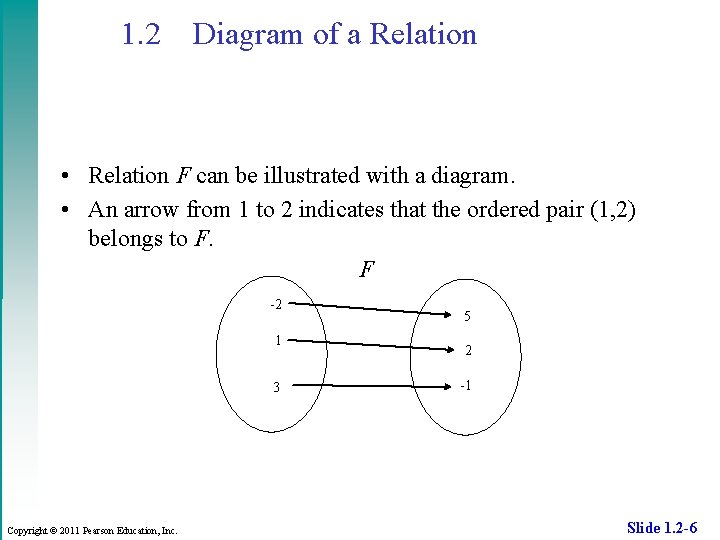
1. 2 Diagram of a Relation • Relation F can be illustrated with a diagram. • An arrow from 1 to 2 indicates that the ordered pair (1, 2) belongs to F. F -2 1 3 Copyright © 2011 Pearson Education, Inc. 5 2 -1 Slide 1. 2 -6

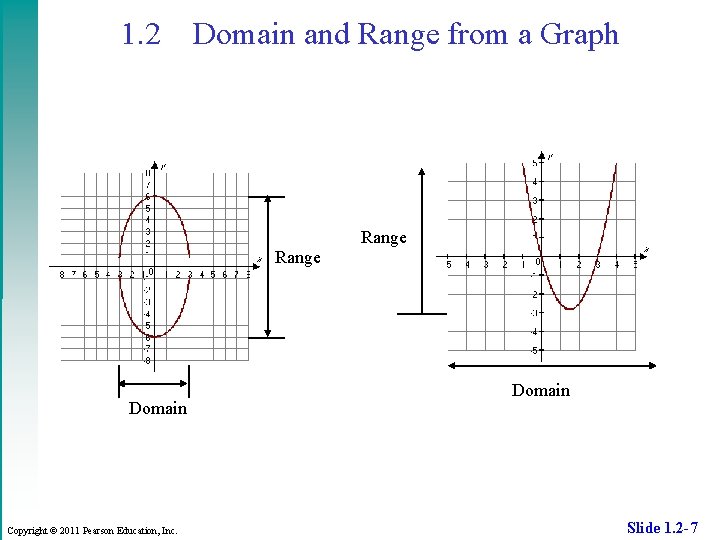
1. 2 Domain and Range from a Graph Range Domain Copyright © 2011 Pearson Education, Inc. Range Domain Slide 1. 2 -7

1. 2 Definition of a Function A function is a relation in which each element in the domain corresponds to exactly one element in the range. If x represents any element in the domain, then x is called the independent variable. If y represents any element in the range, then y is called the dependent variable. Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -8

1. 2 Definition of a Function Examples Indicate whether the following relations are functions. 1. 2. Copyright © 2011 Pearson Education, Inc. {(1, 1), (1, 2), (1, 3), (2, 4)} x -4 -3 -2 -1 0 1 y 2 2 2 Yes, since each element in the domain corresponds to exactly one element in the range. Slide 1. 2 -9

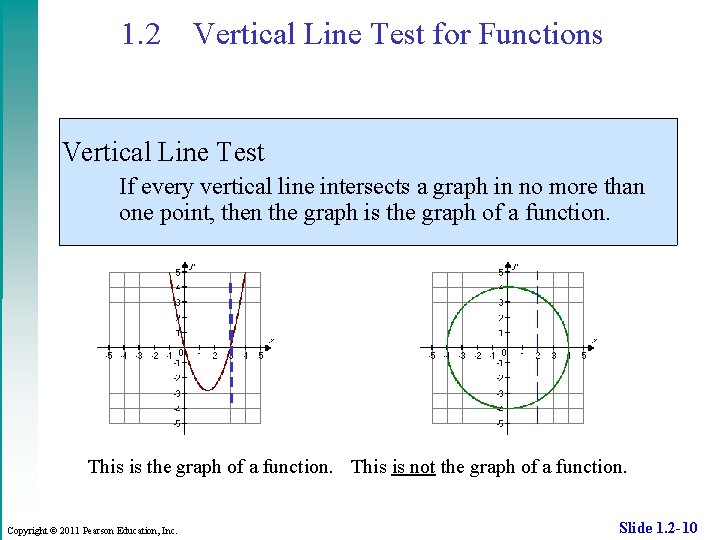
1. 2 Vertical Line Test for Functions Vertical Line Test If every vertical line intersects a graph in no more than one point, then the graph is the graph of a function. This is the graph of a function. This is not the graph of a function. Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -10

1. 2 Definition of a Function (Alternative Definition) A function is a correspondence in which each element x from a set called the domain is paired with one and only one element y from a set called the range. Copyright © 2011 Pearson Education, Inc. Slide 1. 2 -11