1 2 George Dantzig Autor do mtodo SIMPLEX

































- Slides: 69

1

2

George Dantzig Autor do método SIMPLEX, é considerado o “Pai” da Programação Linear. O método SIMPLEX é considerado como um dos mais significativos avanços da matemática no século XX. 3

SITUAÇÃO (ver lição PL 2) Uma empresa necessita produzir os produtos P 1 e P 2 que vende com margem de lucro unitário médio, de 10€ e 6€ respectivamente. Para o produto P 1 estão agendadas 35 horas de trabalho sabendo-se que, tecnicamente, a produção de uma unidade de P 1 requer em média 5 horas. As encomendas em carteira, para o produto P 2, aconselham a não produzir mais do que 7 unidades. No que respeita à matéria prima a utilizar o estoque existente é de 40 kg sendo o consumo de 5 kg por unidade produzida de P 1 ou P 2. A empresa pretende OTIMIZAR a produção de P 1 e P 2 visando a maximização do lucro. 4

Modelo de Programação Linear para otimizar a produção de P 1 e P 2 (apresentado na lição PL_2) Max f(X)=10 x 1 + 6 x 2 (lucro a maximizar) sujeito a: 5 x 1 < 35 x 2 < 7 (35 h para a produção de P 1; 5 h por unidade produzida) (produção de P 2 não deve exceder 7 unidades) 5 x 1 + 5 x 2 < 40 x 1 , x 2 > 0 (40 kg de MP para a produção; consumos de 5 kg por unidade produzida de P 1 ou P 2) (nível da produção de P 1 e P 2 respectivamente) Nota: Modelo apresentado na PL_2. Copie o modelo para consulta posterior. 5

Modelo na forma padrão do Simplex (apresentada na lição PL_3) Max f(X)=10 x 1 + 6 x 2 + 0 F 1 + 0 F 2 + 0 F 3 sujeito a: 5 x 1 + F 1 = 35 (restrição do tipo < equilibra com variável de FOLGA) x 2 + F 2 = 7 (restrição do tipo 5 x 1 + 5 x 2 + F 3 = 40 < equilibra com variável de FOLGA) (restrição do tipo < equilibra com variável de FOLGA) x 1 , x 2 , F 1 , F 2 , F 3 > 0 (não negatividade) 6

Forma Padrão: Registar as variáveis da forma padrão Quadro Inicial do Simplex 7

Forma Padrão: Registar as variáveis da forma padrão x 1 x 2 F 1 F 2 F 3 8

Forma Padrão: Coluna para Valor do Segundo Membro x 1 x 2 F 1 F 2 F 3 9

Forma Padrão: x 1 x 2 F 1 F 2 F 3 VSM 10

Forma Padrão: Linhas para registro das equações x 1 x 2 F 1 F 2 F 3 VSM 11

Forma Padrão: Linhas para registro das equações x 1 x 2 F 1 F 2 F 3 VSM 5 0 1 5 1 0 0 0 1 35 7 40 12

Forma Padrão: Linha para registro de f(X) x 1 x 2 F 1 F 2 F 3 VSM 5 0 1 5 1 0 0 0 1 35 7 40 13

Forma Padrão: Notar a movimentação das variáveis para o 1º membro (coeficientes simétricos no quadro) x 1 x 2 F 1 F 2 F 3 VSM 5 0 0 1 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 14

Forma Padrão: Coluna para registrar as Variáveis Básicas da solução x 1 x 2 F 1 F 2 F 3 VSM 5 0 0 1 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 15

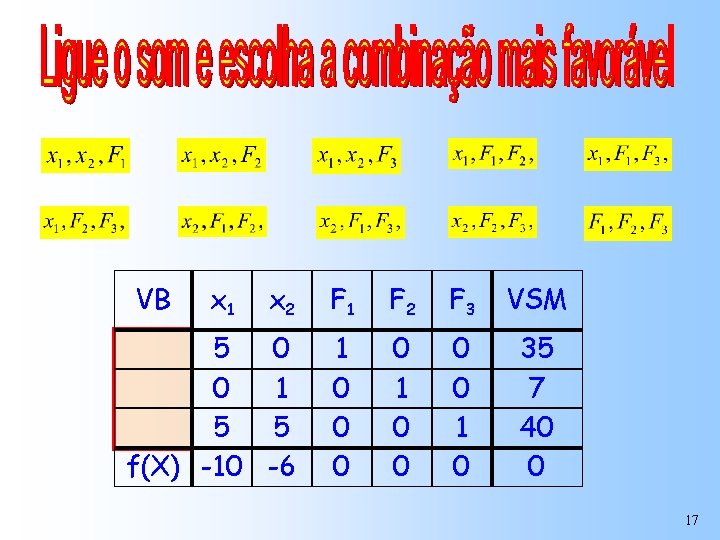
Forma Padrão: Campo para registrar as Variáveis Básicas da 1ª solução VB x 1 x 2 F 1 F 2 F 3 VSM 5 0 0 1 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 16

VB x 1 x 2 F 1 F 2 F 3 VSM 5 0 0 1 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 17

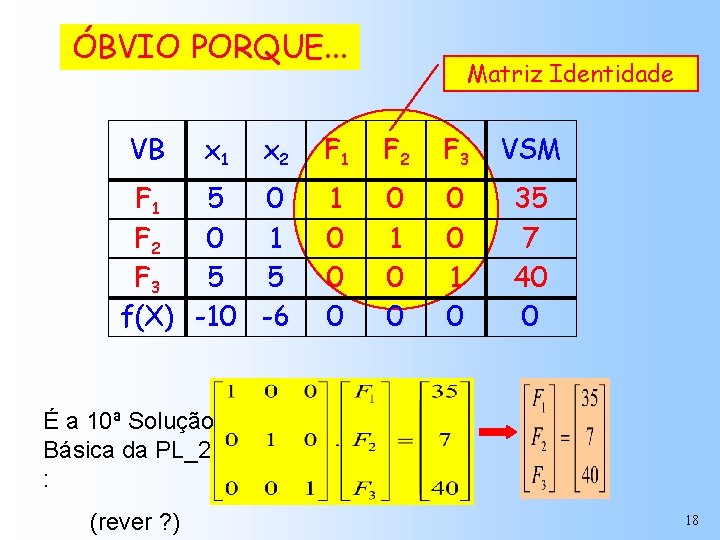
ÓBVIO PORQUE. . . VB x 1 Matriz Identidade x 2 F 1 F 2 F 3 VSM 5 0 F 1 0 1 F 2 F 3 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 É a 10ª Solução Básica da PL_2 : (rever ? ) 18

Conjunto dos Vetores das VB é Matriz Identidade VB x 1 x 2 F 1 F 2 F 3 VSM F 1 5 0 0 1 F 2 F 3 5 5 f(X) -10 -6 1 0 0 0 0 1 0 35 7 40 0 LEITURA DIRETA DA SOLUÇÃO F 1 35 7 40 f(X) 0 F 2 F 3 19

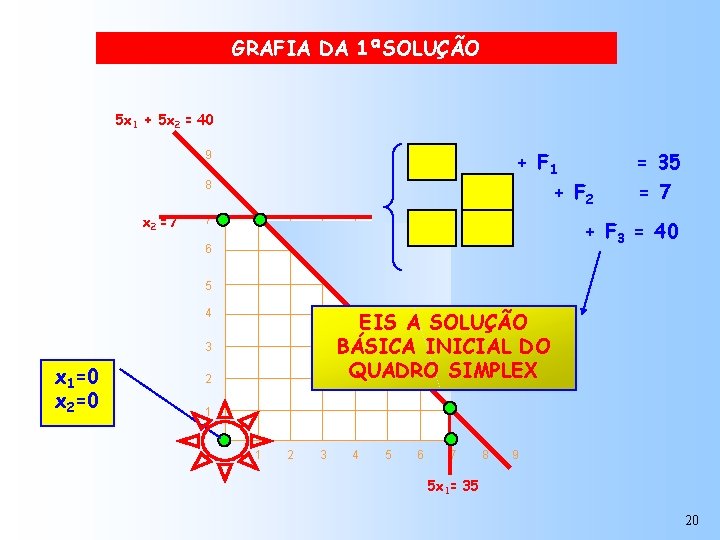
GRAFIA DA 1ªSOLUÇÃO 5 x 1 + 5 x 2 = 40 5 x 1 9 + F 1 x 2 + F 2 8 x 2 =7 7 5 x 1 + 5 x 2 6 = 35 = 7 + F 3 = 40 5 4 EIS A SOLUÇÃO BÁSICA INICIAL DO QUADRO SIMPLEX 3 x 1=0 x 2=0 2 1 1 2 3 4 5 6 7 8 9 5 x 1= 35 20

QUADRO SIMPLEX - 1ª SBA VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Os vetores das VB formam sempre uma matriz Identidade; As VB têm sempre coeficiente nulo na equação de f(X); O valor das VB, F 1, F 2 e F 3 , (solução do sistema de equações técnicas) é lido diretamente na coluna VSM; O valor das VNB (x 1 e x 2) é sempre nulo; O valor de f(X) é lido diretamente na coluna VSM. 21

QUADRO SIMPLEX Valor das variáveis Básicas VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Coeficientes das variáveis na equação da função Valor da função objetivo 22

QUADRO SIMPLEX - 1ª SBA VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Vamos analisar as VNB x 1 e x 2 23

QUADRO SIMPLEX - 1ª SBA VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Esta soma é NULA x 1 é VNB (valor zero) Se x 1 entrar para a base e aumentar o seu valor a função sobe à taxa 10 Se a função sobe então é porque não atingiu o Máximo ou seja a solução não é ótima. 24

QUADRO SIMPLEX - 1ª SBA VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Esta soma é NULA x 2 é VNB (valor zero) Se x 2 entrar para a base e aumentar o seu valor a função sobe à taxa 6 Se a função sobe então é porque não atingiu o Máximo ou seja a solução não é ótima. 25

QUADRO SIMPLEX - 1ª SBA VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 Se na equação de f(X) há variáveis com coeficiente negativo a solução não é ótima Deve entrar para a base a variável com o coeficiente mais negativo. Neste quadro a variável x 1 deve entrar para a base 26

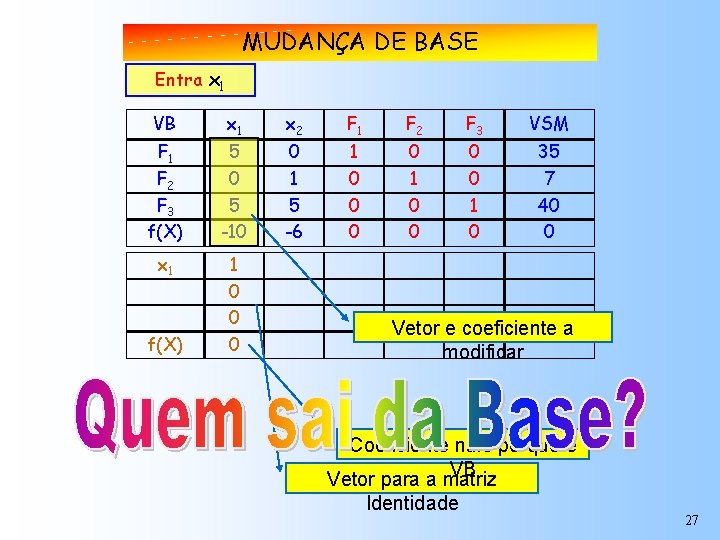
MUDANÇA DE BASE Entra x 1 VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 0 0 f(X) Vetor e coeficiente a modificar Coeficiente nulo porque é VB Vetor para a matriz Identidade 27

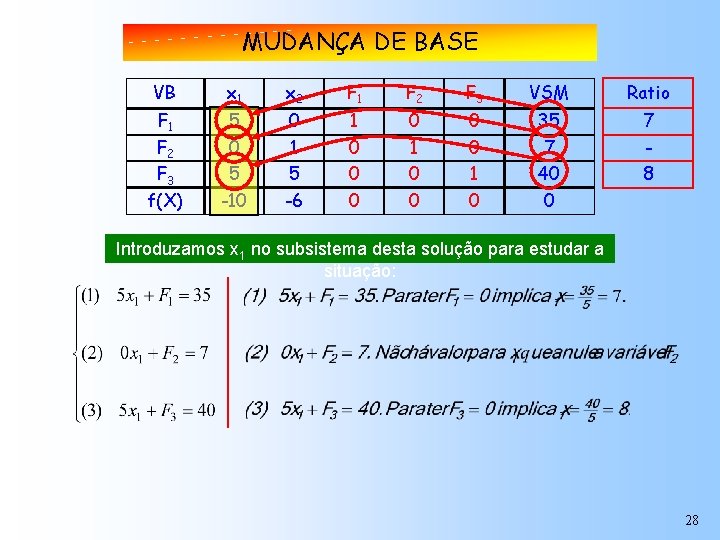
MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 VSM Ratio F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 7 8 Introduzamos x 1 no subsistema desta solução para estudar a situação: 28

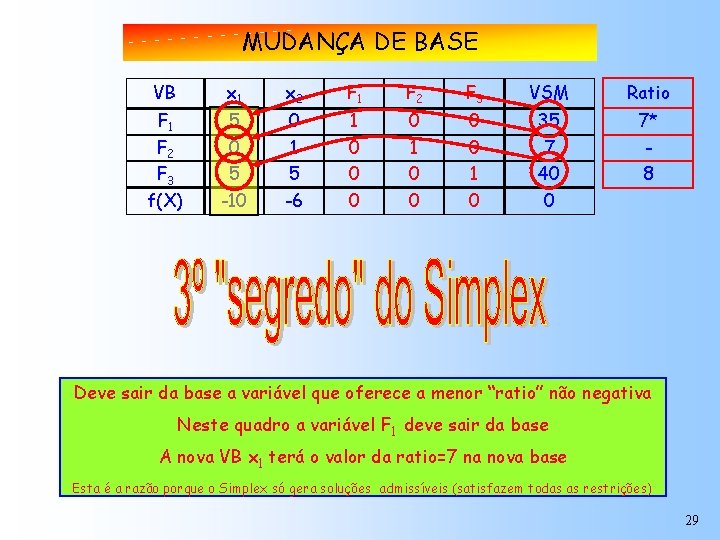
MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 VSM Ratio F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 7* 8 Deve sair da base a variável que oferece a menor “ratio” não negativa Neste quadro a variável F 1 deve sair da base A nova VB x 1 terá o valor da ratio=7 na nova base Esta é a razão porque o Simplex só gera soluções admissíveis (satisfazem todas as restrições) 29

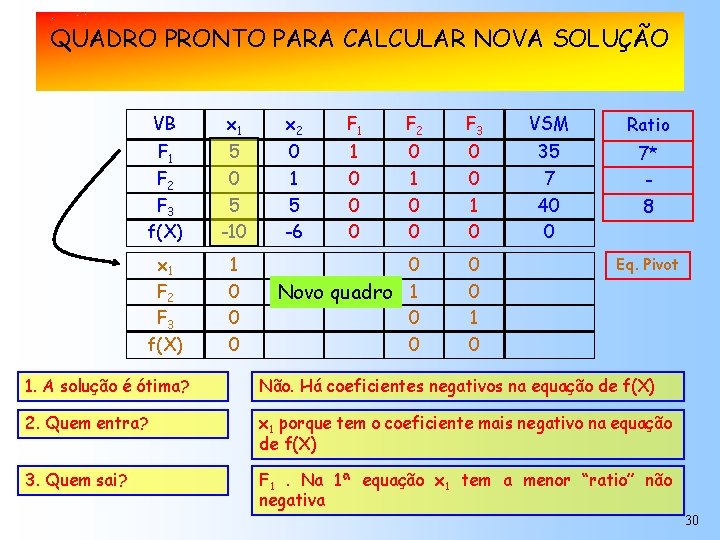
COMO ANALISAR UMACALCULAR SOLUÇÃONOVA DO SIMPLEX QUADRO PRONTO PARA SOLUÇÃO Maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM Ratio F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 7* 8 x 1 F 2 F 3 f(X) 1 0 0 Novo quadro 1 0 0 1 0 Eq. Pivot 1. A solução é ótima? Não. Há coeficientes negativos na equação de f(X) 2. Quem entra? x 1 porque tem o coeficiente mais negativo na equação de f(X) 3. Quem sai? F 1. Na 1ª equação x 1 tem a menor “ratio” não negativa 30

Se não sabe efetuar transformações lineares não continue. Estude bem a lição (PL_3) e depois regresse. 31

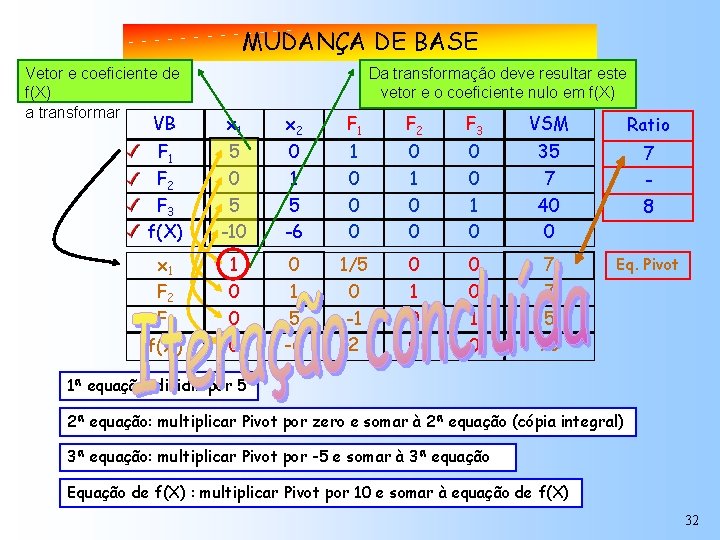
MUDANÇA DE BASE Vetor e coeficiente de f(X) a transformar Da transformação deve resultar este vetor e o coeficiente nulo em f(X) VB x 1 x 2 F 1 F 2 F 3 VSM Ratio F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 7 8 x 1 1 0/5 0 1 1/5 0 0 0 Eq. Pivot 1 0 35/5 7 7 5 10(0)-6 -6 -1 10(1/5)+0 2 0 1 0 0 F 2 F 3 f(X) 0 0 0 -5(0)+5 -5(1/5)+0 5 10(7)+0 70 -5(7)+40 1ª equação: dividir por 5 2ª equação: multiplicar Pivot por zero e somar à 2ª equação (cópia integral) 3ª equação: multiplicar Pivot por -5 e somar à 3ª equação Equação de f(X) : multiplicar Pivot por 10 e somar à equação de f(X) 32

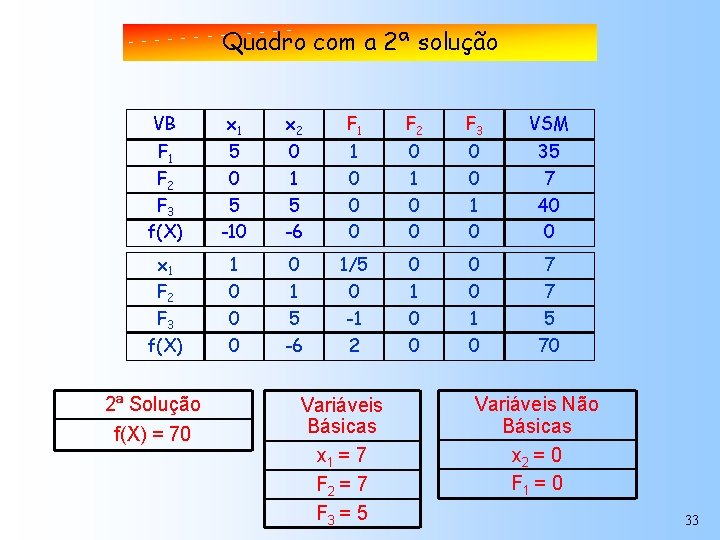
Quadro com a 2ª solução VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 F 3 2ª Solução f(X) = 70 Variáveis Básicas x 1 = 7 F 2 = 7 F 3 = 5 Variáveis Não Básicas x 2 = 0 F 1 = 0 33

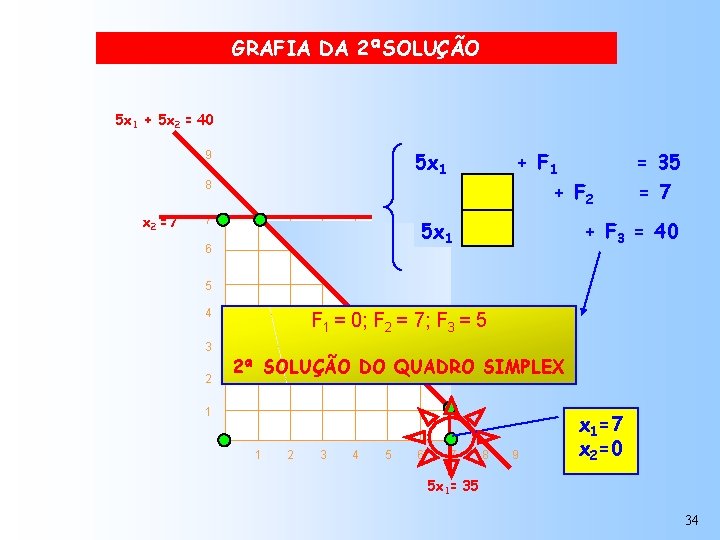
GRAFIA DA 2ªSOLUÇÃO 5 x 1 + 5 x 2 = 40 5 x 1 9 + F 1 x 2 + F 2 8 x 2 =7 7 5 x 1 + 5 x 2 6 = 35 = 7 + F 3 = 40 5 4 3 2 F 1 = 0; F 2 = 7; F 3 = 5 2ª SOLUÇÃO DO QUADRO SIMPLEX 1 1 2 3 4 5 6 7 8 9 x 1=7 x 2=0 5 x 1= 35 34

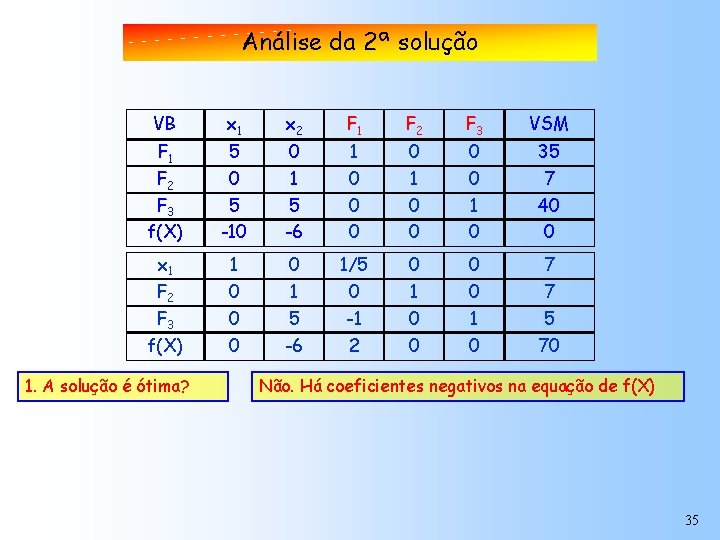
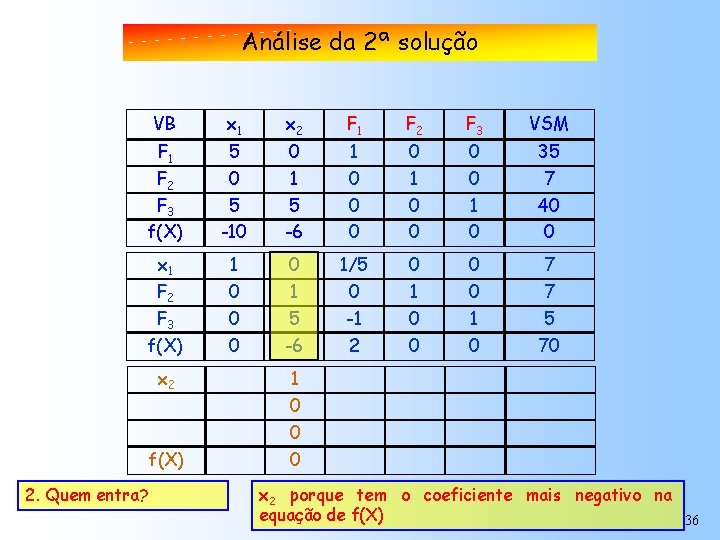
Análise da 2ª solução VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 F 3 1. A solução é ótima? Não. Há coeficientes negativos na equação de f(X) 35

Análise da 2ª solução VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 F 3 x 2 f(X) 2. Quem entra? 1 0 0 0 x 2 porque tem o coeficiente mais negativo na equação de f(X) 36

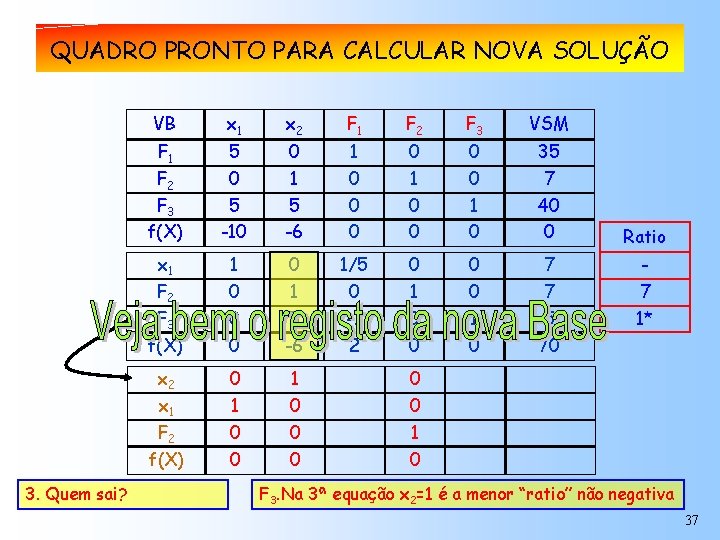
Análise 2ª solução. NOVA SOLUÇÃO QUADRO PRONTO PARAda CALCULAR VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 x 1 0 1 1 F 2 f(X) 3. Quem sai? 0 0 0 Ratio 7 1* 0 0 1 0 F 3. Na 3ª equação x 2=1 é a menor “ratio” não negativa 37

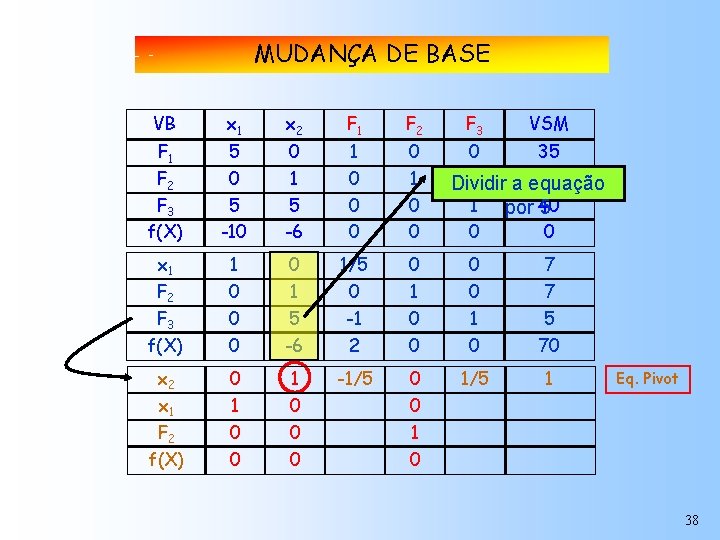
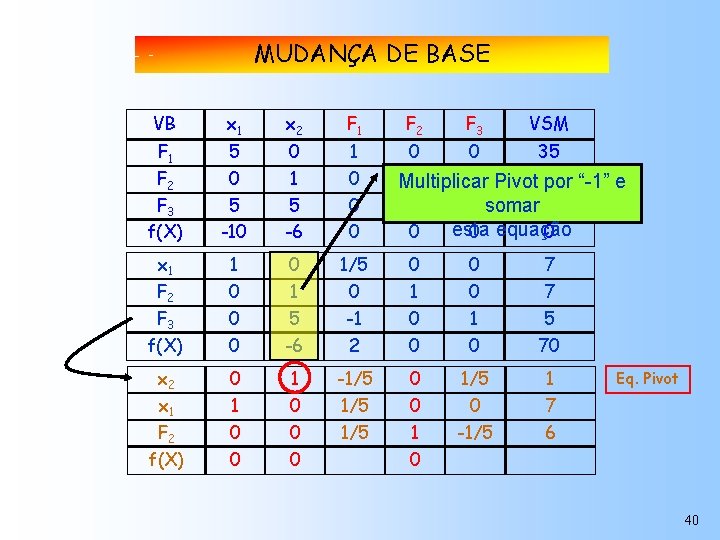
MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 -1/5 0 1/5 5/5 1 1 0 0 F 2 0 0 1 0 0 0 x 1 f(X) F 3 VSM 0 35 0 7 Dividir a equação 1 por 40 5 0 0 Eq. Pivot 38

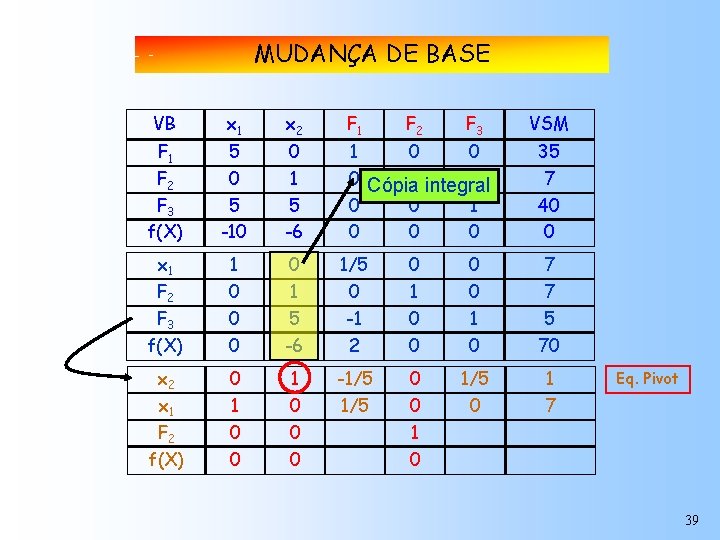
MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 Cópia 1 integral 0 0 0 1 0 0 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 0 -1/5 1/5 0 1 7 F 2 0 0 1 0 0 0 x 1 f(X) F 2 0 F 3 VSM 35 7 40 0 Eq. Pivot 39

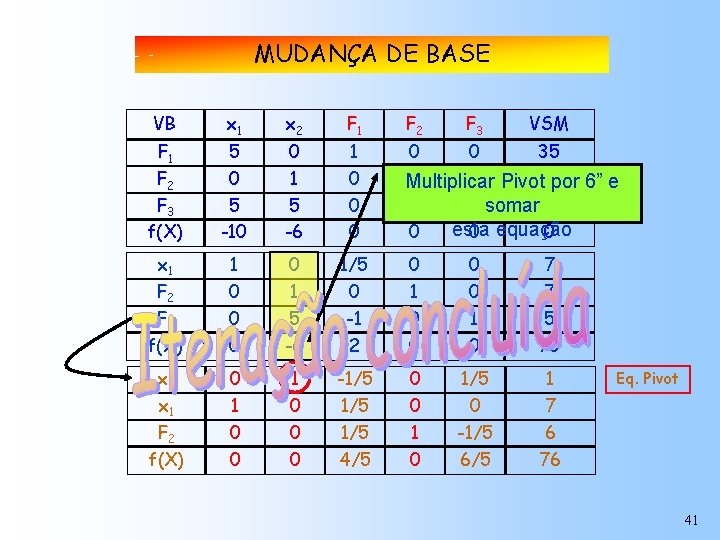
MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 -1/5 0 1/5 1 1 0 0 F 2 0 0 1/5 0 -1/5 7 6 0 0 x 1 f(X) F 2 F 3 VSM 0 0 35 1 0 Pivot 7 Multiplicar por “-1” e 0 1 somar 40 esta 0 0 equação 0 1 Eq. Pivot 0 40

MUDANÇA DE BASE VB x 1 x 2 F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 35 1 0 Pivot 7 por 6” e Multiplicar 0 1 somar 40 esta 0 0 equação 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 -1/5 0 1/5 1 1 0 1/5 0 0 7 F 2 0 0 1/5 4/5 -1/5 6 76 x 1 f(X) 0 F 3 VSM Eq. Pivot 41

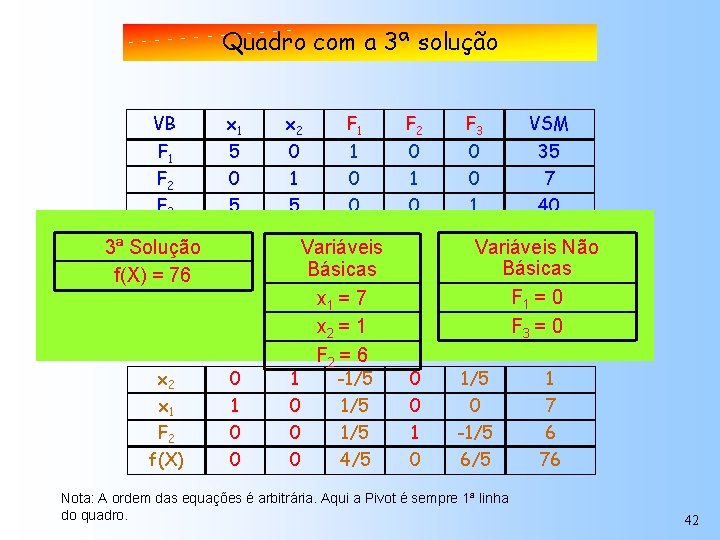
Quadro com a 3ª solução VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 0 70 3ª Solução x f(X) = 176 1 F 2 0 F 3 0 f(X) 0 x 2 0 F 2 x 1 f(X) Variáveis 0 Básicas 1/5 1 x =07 1 5 x =-11 2 -6 2 F 2 = 6 0 1 0 0 Variáveis Não 0 Básicas 7 0 F 1 =70 1 F 3 =50 1 -1/5 0 1/5 1 1 0 1/5 0 0 7 0 0 1/5 1 -1/5 6 0 0 4/5 0 6/5 76 Nota: A ordem das equações é arbitrária. Aqui a Pivot é sempre 1ª linha do quadro. 42

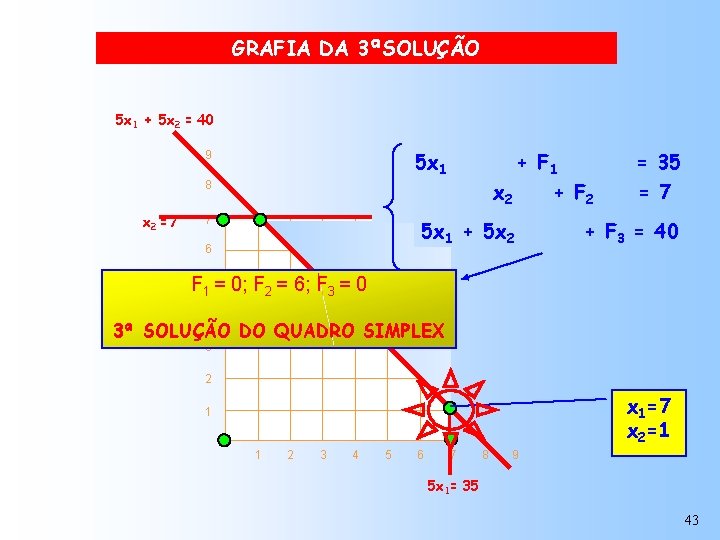
GRAFIA DA 3ªSOLUÇÃO 5 x 1 + 5 x 2 = 40 5 x 1 9 + F 1 x 2 + F 2 8 x 2 =7 7 5 x 1 + 5 x 2 6 = 35 = 7 + F 3 = 40 F 15 = 0; F 2 = 6; F 3 = 0 4 3ª SOLUÇÃO DO QUADRO SIMPLEX 3 2 x 1=7 x 2=1 1 1 2 3 4 5 6 7 8 9 5 x 1= 35 43

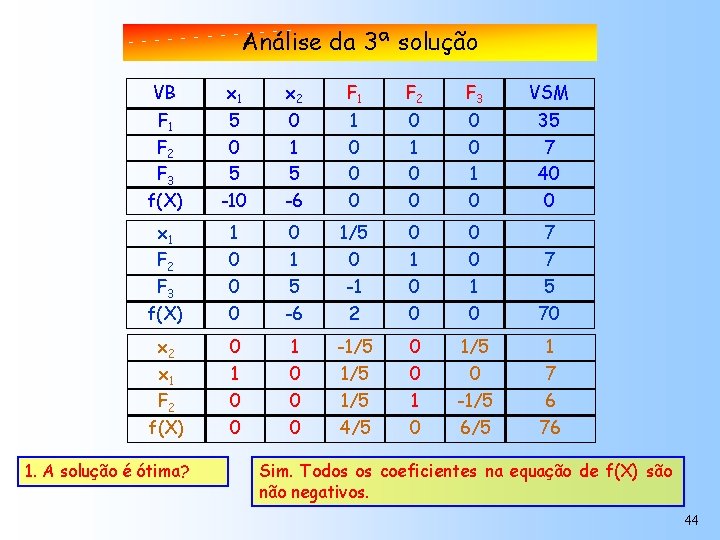
Análise da 3ª solução VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 -1/5 0 1/5 1 1 0 1/5 0 0 7 F 2 0 0 1/5 1 -1/5 6 0 0 4/5 0 6/5 76 x 1 f(X) 1. A solução é ótima? Sim. Todos os coeficientes na equação de f(X) são negativos. 44

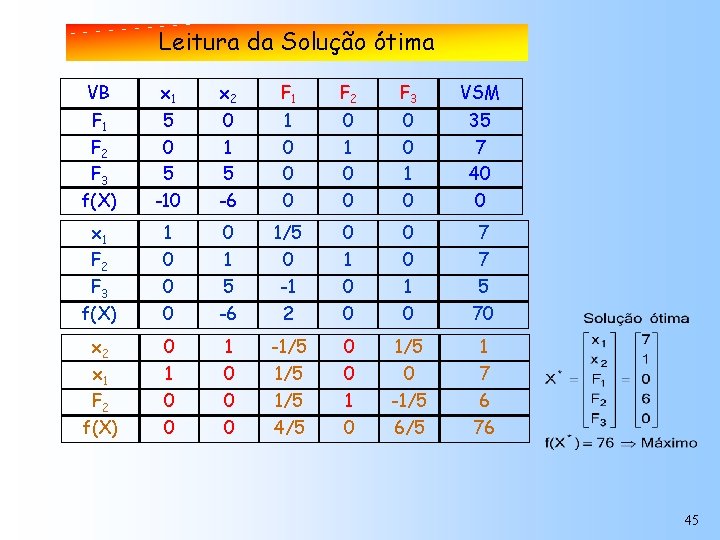
Leitura da Solução ótima VB x 1 x 2 F 1 F 2 F 3 VSM F 1 F 2 F 3 f(X) 5 0 5 -10 0 1 5 -6 1 0 0 0 0 1 0 35 7 40 0 x 1 1 0 1/5 0 0 7 F 2 0 1 0 7 F 3 0 5 -1 0 1 5 f(X) 0 -6 2 0 0 70 x 2 0 1 -1/5 0 1/5 1 1 0 1/5 0 0 7 F 2 0 0 1/5 1 -1/5 6 0 0 4/5 0 6/5 76 x 1 f(X) 45

Resumo do Método Simplex (Maximização) 1. Solução Inicial Escolher para VB as variáveis auxiliares cujos vetores constituem uma matriz Identidade; 2. Escolher a Nova VB Identificar as variáveis não básicas que na equação da função têm coeficiente negativo. Destas variáveis selecionar para entrada na base aquela cujo coeficiente tem maior valor absoluto. Se houver mais do que uma variável nas mesmas condições escolher arbitrariamente. 3. Escolher a Nova VNB Se todas as variáveis têm coeficiente não negativo então a solução corrente Nas equações técnicas calcular os quocientes entre os valores da solução é ótima. corrente (coluna VSM) e os coeficientes não negativos da nova VB (ignorar quocientes com denominador nulo ou negativo). A VB corrente em cuja linha se verifica o menor destes quocientes é aquela que deve sair da base. Se este mínimo se verificar em mais do que uma das VB correntes, escolher arbitrariamente uma delas para nova VNB. 4. Calcular o novo quadro do Simplex Efetuar transformações lineares para que o vetor dos coeficientes da nova VB juntamente com os das VB que permanecem na base constituam uma matriz Identidade. Todas as VB devem ter coeficiente nulo na equação da função. 5. Voltar ao Passo 2 46

SOFTWARE – APOIO ACADÉMICO Utilize o software do Método Simplex para apoio do estudo. Tem disponível no site da disciplina de Pesquisa Operacional I (Teleduc) 47

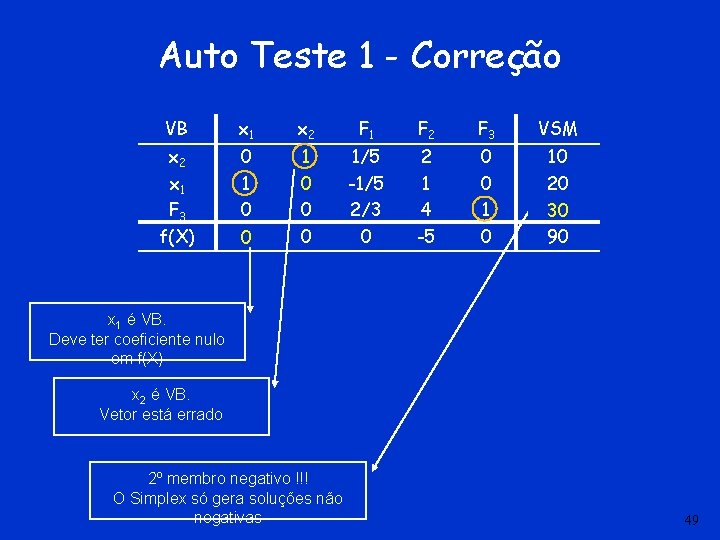
Auto Teste 1 (maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 1 0 -10 0 1/5 -1/5 2/3 0 2 1 4 -5 0 0 10 20 -30 90 Neste quadro Simplex há erros? SIM NÃO (LIGUE O SOM) 48

Auto Teste 1 - Correção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 1 0 -10 0 0 1 1 0 0 0 1/5 -1/5 2/3 0 2 1 4 -5 0 0 10 20 -30 30 90 x 1 é VB. Deve ter coeficiente nulo em f(X) x 2 é VB. Vetor está errado 2º membro negativo !!! O Simplex só gera soluções não negativas 49

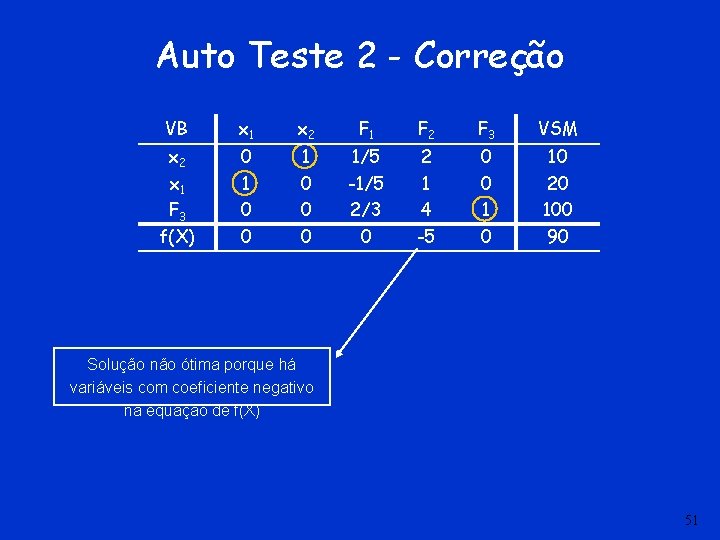
Auto Teste 2 (maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 1 0 0 0 1/5 -1/5 2/3 0 2 1 4 -5 0 0 10 20 100 90 Solução ótima em Maximização SIM NÃO (LIGUE O SOM) 50

Auto Teste 2 - Correção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 1 0 0 0 1/5 -1/5 2/3 0 2 1 4 -5 0 0 10 20 100 90 Solução não ótima porque há variáveis com coeficiente negativo na equação de f(X) 51

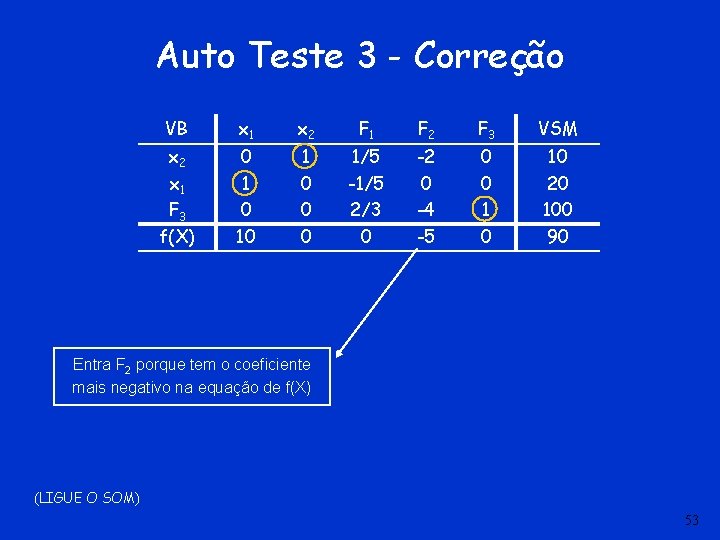
Auto Teste 3 VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 0 -2 0 -4 -5 0 0 10 20 100 90 Solução não ótima (em Maximização). Entra para a base a variável F 2 SIM NÃO (LIGUE O SOM) 52

Auto Teste 3 - Correção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 0 -2 0 -4 -5 0 0 10 20 100 90 Entra F 2 porque tem o coeficiente mais negativo na equação de f(X) (LIGUE O SOM) 53

Auto Teste 4 (maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 0 -2 0 -4 -5 0 0 10 20 100 90 Sai da base a variável F 3 SIM NÃO (LIGUE O SOM) 54

Auto Teste 4 - Correcção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 0 -2 0 -4 -5 0 0 10 20 100 90 Não é possível mudar de base porque não há “ratio” finita e não negativa. Não há pois limite superior para a variável F 2 (selecionada para entrar). Nesta situação a função objetivo tem valor Ilimitado. 55

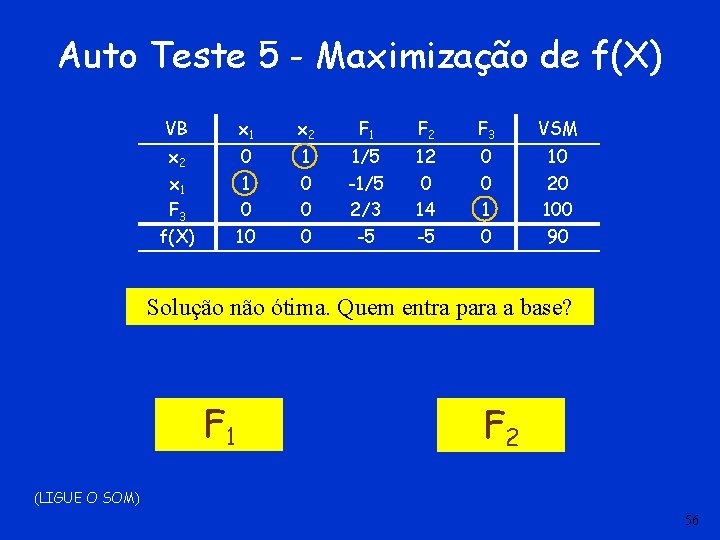
Auto Teste 5 - Maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 -5 12 0 14 -5 0 0 10 20 100 90 Solução não ótima. Quem entra para a base? F 1 F 2 (LIGUE O SOM) 56

Auto Teste 5 - Correção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 1/5 -1/5 2/3 -5 12 0 14 -5 0 0 10 20 100 90 Entra para a base a variável com coeficiente mais negativo. Em caso de empate a escolha é arbitrária. Neste caso pode escolher-se F 1 ou F 2 (LIGUE O SOM) 57

Auto Teste 6 - Maximização de f(X) VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 -1/5 -2/3 5 12 0 14 5 0 0 10 20 100 90 Solução Ótima. O Espaço de Soluções é Limitado Ilimitado (LIGUE O SOM) 58

Auto Teste 6 - Correção VB x 1 x 2 F 1 F 2 F 3 VSM x 2 x 1 F 3 f(X) 0 10 1 0 0 0 -1/5 -2/3 5 12 0 14 5 0 0 10 20 100 90 Atingido o ótimo se algum dos vetores das VNB tiver apenas coordenadas não positivas é sinal de espaço de soluções ILIMITADO. É o que sucede neste caso (vetor F 1). Um espaço de soluções ILIMITADO pode ter soluções limitadas. Neste caso o espaço de soluções é ILIMITADO mas tem 59

Resumo do Método Simplex (Maximização) 1. Solução Inicial Escolher para VB as variáveis auxiliares cujos vetores constituem uma matriz Identidade 2. Escolher a Nova VB Identificar as variáveis não básicas que na equação da função têm coeficiente negativo. Destas variáveis selecionar para entrada na base aquela cujo coeficiente tem maior valor absoluto. Se houver mais do que uma variável nas mesmas condições escolher arbitrariamente. Se todas as variáveis têm coeficiente não negativo então a solução corrente é ótima. 3. Escolher a Nova VNB Nas equações técnicas calcular os quocientes entre os valores da solução corrente (coluna VSM) e os coeficientes não negativos da nova VB (ignorar quocientes com denominador nulo ou negativo). A VB corrente em cuja linha se verifica o menor destes quocientes é aquela que deve sair da base. Se este mínimo se verificar em mais do que uma das VB correntes, escolher arbitrariamente uma delas para nova VNB. 4. Calcular o novo quadro do Simplex 60

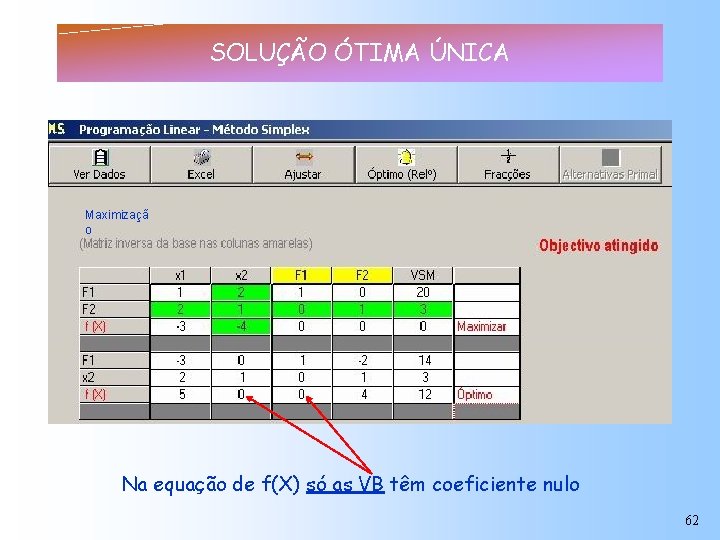
Classificação da Solução ótima ÚNICA Na equação de f(X) só as VB têm coeficiente nulo INDETERMINADA (solução múltipla) Na equação de f(X) há VNB com coeficiente nulo 61

SOLUÇÃO ÓTIMA ÚNICA Maximizaçã o Na equação de f(X) só as VB têm coeficiente nulo 62

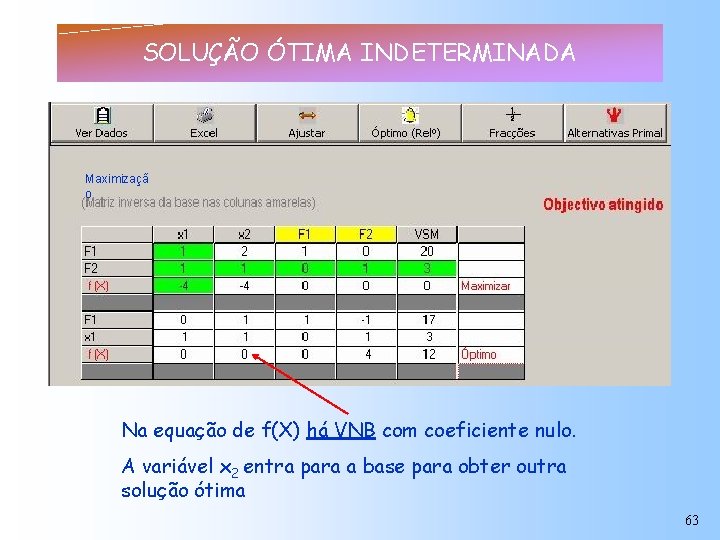
SOLUÇÃO ÓTIMA INDETERMINADA Maximizaçã o Na equação de f(X) há VNB com coeficiente nulo. A variável x 2 entra para a base para obter outra solução ótima 63

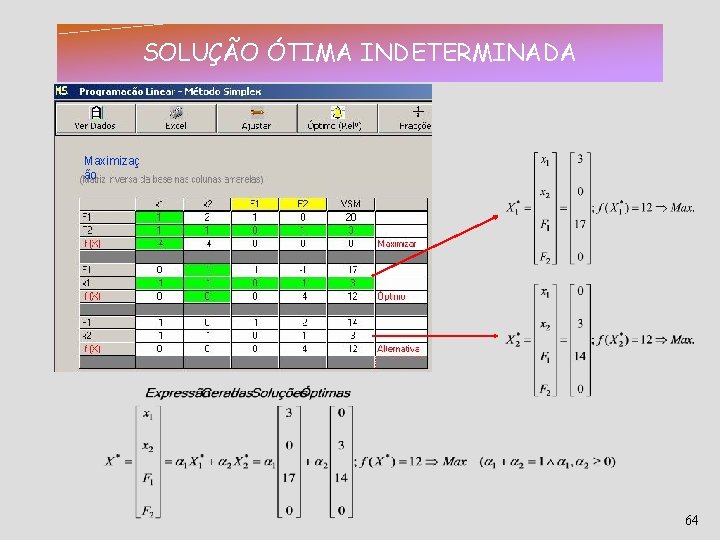
SOLUÇÃO ÓTIMA INDETERMINADA Maximizaç ão 64

REGRAS DA MINIMIZAÇÃO A diferença relativamente à Maximização reside apenas na análise dos coeficientes da função objetivo. A solução é Ótima quando, Má na equação de f(X) todos os coeficiente são não x negativos na equação de f(X) todos os coeficiente são não Mín positivos 65

REGRAS DA MINIMIZAÇÃO Solução não ótima A diferença relativamente à Maximização reside apenas na análise dos coeficientes da função objetivo. Quem entra para a base? Má Variável com coeficiente mais negativo na x equação de f(X) Variável com coeficiente mais positivo na equação Mín de f(X) 66

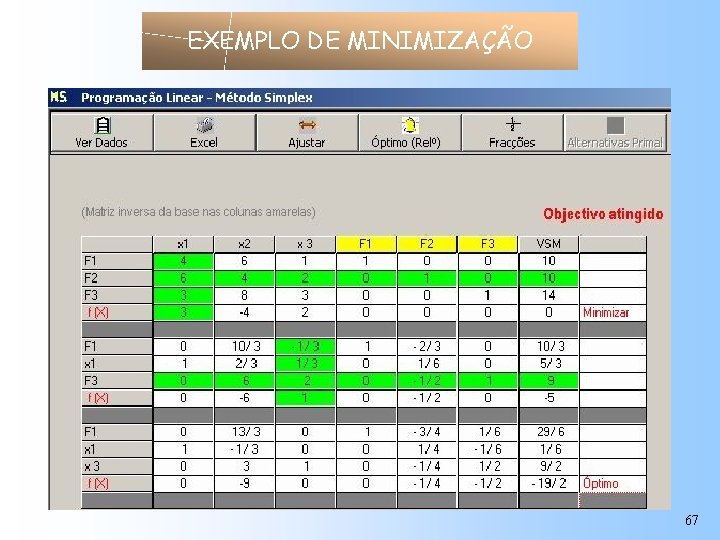
EXEMPLO DE MINIMIZAÇÃO 67

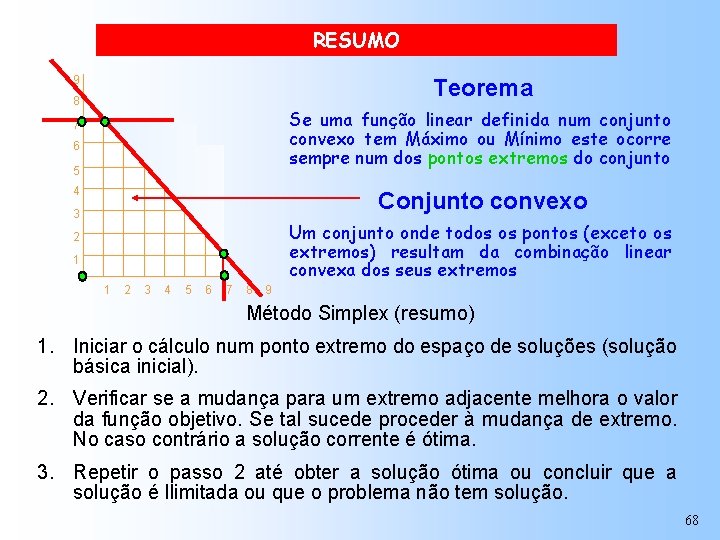
RESUMO 9 Teorema 8 Se uma função linear definida num conjunto convexo tem Máximo ou Mínimo este ocorre sempre num dos pontos extremos do conjunto 7 6 5 4 Conjunto convexo 3 Um conjunto onde todos os pontos (exceto os extremos) resultam da combinação linear convexa dos seus extremos 2 1 1 2 3 4 5 6 7 8 9 Método Simplex (resumo) 1. Iniciar o cálculo num ponto extremo do espaço de soluções (solução básica inicial). 2. Verificar se a mudança para um extremo adjacente melhora o valor da função objetivo. Se tal sucede proceder à mudança de extremo. No caso contrário a solução corrente é ótima. 3. Repetir o passo 2 até obter a solução ótima ou concluir que a solução é Ilimitada ou que o problema não tem solução. 68

69