1 2 Functions and Their Properties Today you

1. 2 Functions and Their Properties Today you will be able to: • Represent functions numerically, algebraically, and graphically • Determine the domain and range for functions • Analyze function characteristics such as extreme values, symmetry, asymptotes, and end behavior.

Parts of a Function • Variables • These are the quantities in a function that can change • Dependent Variables • Depends on another quantity (y-values) • Independent Variables • These quantities tend to have an affect on the dependent variable. (x-values)

Parts of a Function - Example • Variables • Time and temperature • Dependent Variables • Temperature (depends on the time of day) • Independent Variables • Time (is unaffected by the temperature) • Relating Variables • Often written as a ordered pair with the independent variable first (time, temperature)

Notation of a Function • In general we use x to represent the independent variable and y to represent the dependent variable. • We write… y = f(x) meaning y is a function of x T = f(t) meaning Temperature is a function of time

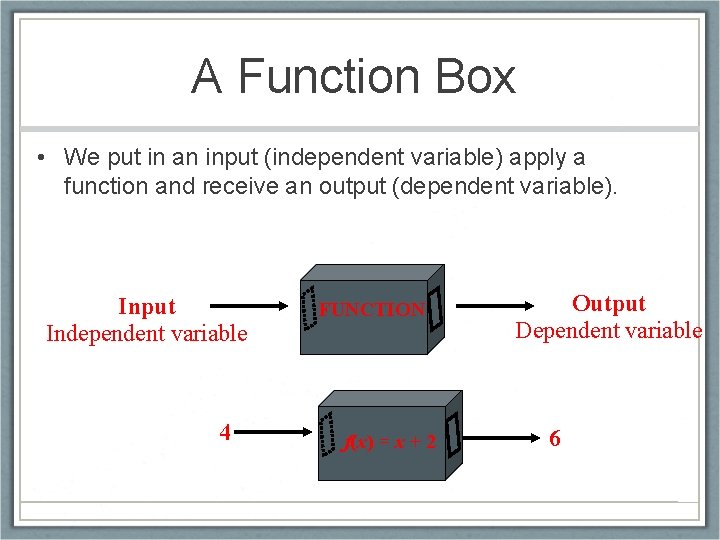
A Function Box • We put in an input (independent variable) apply a function and receive an output (dependent variable). Input Independent variable 4 FUNCTION f(x) = x + 2 Output Dependent variable 6

Domain and Range • Setting up our graph • While the coordinate plane continues infinitely in all directions, most data will not. • Therefore we must determine a logical domain for the independent data. • Domain: the set of logical values for the independent variable • This will affect the range of values that make-up the dependent variable • Range: the set of values for the dependent variable that correspond to specific independent variables

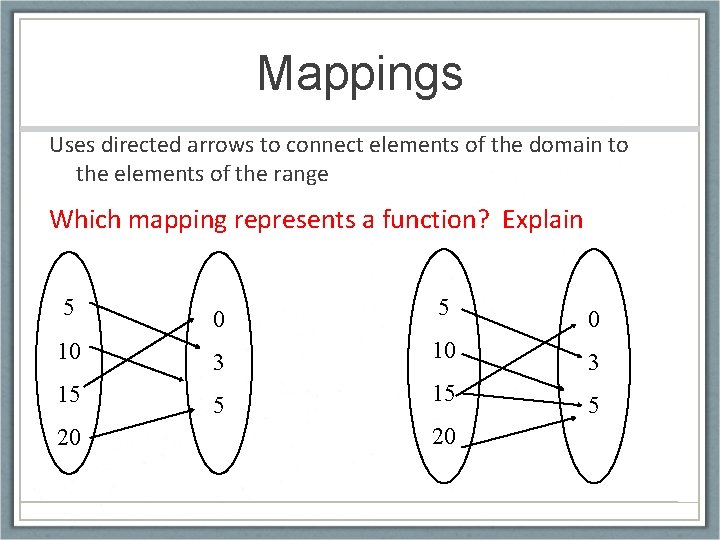
Mappings Uses directed arrows to connect elements of the domain to the elements of the range Which mapping represents a function? Explain 5 0 10 3 15 5 20 5 10 15 20 0 3 5

Ex 2 Does x = 2 y 2 define y as a function of x? Vertical Line Test A graph (set of points (x, y)) in the xy-plane defines y as a function of x if and only if no vertical line intersects the graph in more than one point.

What is your domain? • Implied domain – the domain of a function defined by an algebraic expression • Relevant domain – the domain that fits a given situation For example: • s 2 has implied domain of all real numbers • However, if A = s 2 is the area of a square then the relevant domain is only non-negative real numbers.

Pair with a neighbor to find the domain of each function. , where A(s) is the area of an equilateral triangle with side of length s.

Finding Range Ex 4 Find the range of f(x) = 10 – x 2.

Graphs of functions in reverse Sketch the graph of a function that has a domain: [-5, -1] u (2, 4] and range: [-4, -1] u [1, ∞).

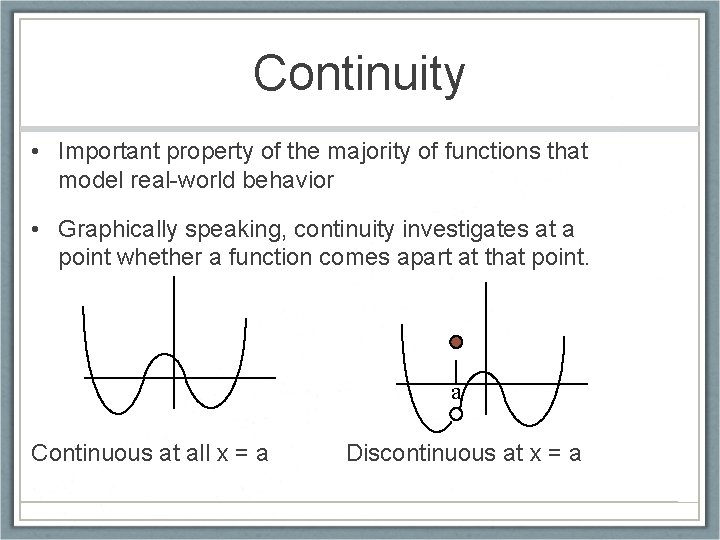
Continuity • Important property of the majority of functions that model real-world behavior • Graphically speaking, continuity investigates at a point whether a function comes apart at that point. a Continuous at all x = a Discontinuous at x = a

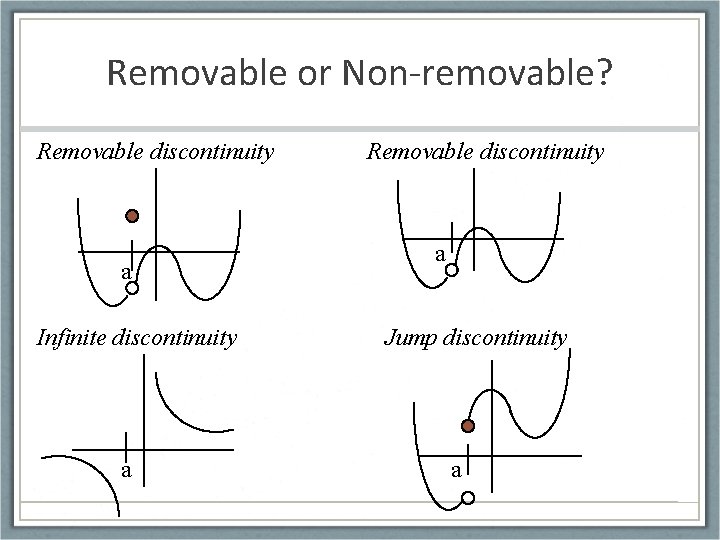
Removable or Non-removable? Removable discontinuity a Infinite discontinuity a Removable discontinuity a Jump discontinuity a

Graph each of the following. Which of the following are discontinuous at x = 2? Are any of the discontinuities removable? a) b) c)

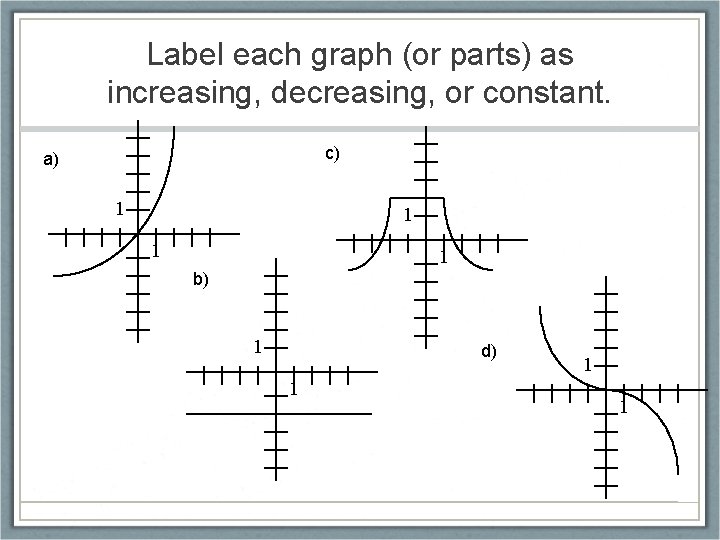
Increasing, Decreasing, and Constant Function on an Interval • A function f is increasing on an interval if, for any two points in the interval, a positive change in x results in a positive change in f(x). • A function f is decreasing on an interval if, for any two points in the interval, a positive change in x results in a negative change in f(x). • A function f is constant on an interval if, for any two points in the interval, a positive change in x results in a zero change in f(x).

Label each graph (or parts) as increasing, decreasing, or constant. c) a) 1 1 b) 1 d) 1 1 1

Tell the intervals on which each function is increasing and the intervals on which it is decreasing. f(x) = (x - 2)2 g(x) = x 2 - 1

Boundedness • A function f is bounded below if there is some number b that is less than or equal to every number in the range of f. Any such number b is called a lower bound of f. • A function f is bound above if there is some number B that is greater than or equal to every number in the range of f. Any such number B is called an upper bound of f. • A function f is bounded it is bounded both above and below.

Ex 9 Identify each of these functions as bounded below, bounded above, or bounded. w(x) = -3 x 2 + 4 p(x) = x x 2+1

Local and Absolute Extrema • If f(x) is greater than or equal to all range values of f, then f(c) is the maximum (or absolute maximum) value of f. • If f(x) is less than or equal to all range values of f, then f(c) is the minimum (or absolute minimum) value of f. • Local extrema are also called relative extrema.

Ex 10 Decide whether f(x) = x 4 – 7 x 2 + 6 x has any local extrema.

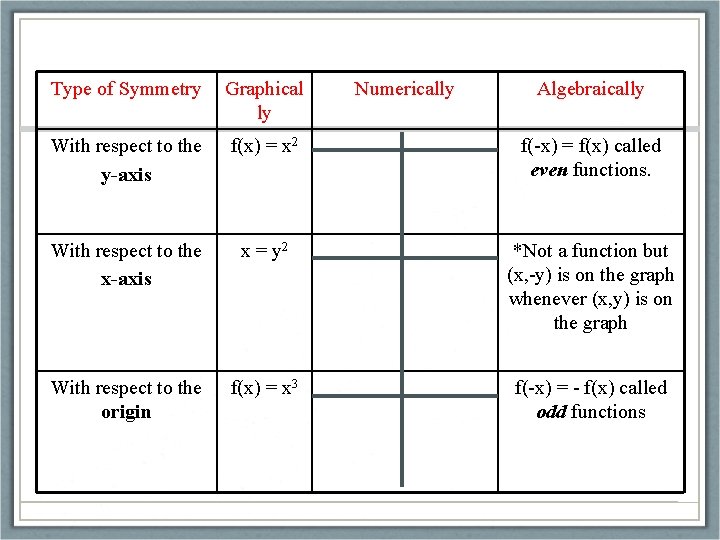
Symmetry • A graph appears identical when viewed on either side of a line or through a point. • Symmetry can be easily viewed graphically, numerically, or algebraically.

Type of Symmetry Graphical ly Numerically Algebraically With respect to the y-axis f(x) = x 2 f(-x) = f(x) called even functions. With respect to the x-axis x = y 2 *Not a function but (x, -y) is on the graph whenever (x, y) is on the graph With respect to the origin f(x) = x 3 f(-x) = - f(x) called odd functions

Ex 11 Tell whether each of the following functions is even, odd, or neither. a) f(x) = x 2 – 3 b) g(x) = x 2 – 2 x – 2 c) h(x) = x 3 4 – x 2

Asymptotes • The line y = b is a horizontal asymptote of the graph of a function y = f(x) if f(x) approaches a limit of b as x approaches +∞ or - ∞. • In limit notation, • The line x = a is a vertical asymptote of the graph of a function y = f(x) if f(x) approaches a limit of + ∞ or -∞ as x approaches a from either direction. • In limit notation,

Horizontal Asymptotes Rule #1: If the numerator and the denominator have the same degree then: • HA: y = Leading Coefficient • Example: f(x) = 3 x 2 x + 5

Horizontal Asymptote Rule #2: If the degree of the numerator is less than the degree of the denominator then: • HA: y = 0 • Example: f(x) = 3 x 3 + 7 x -2 x 5 +18 x 4 -3 x HA = y = 0

Horizontal Asymptote Rule #3: The degree of the numerator is greater the degree of the denominator: HA: y = DNE • Example: f(x) = 18 x 3 2 x 2 + 7

Ex 12 Identify any vertical or horizontal asymptotes by viewing each graph and observing its end behavior.

Tonight’s Assignment • P. 98 -100 Ex 3 -66 m. of 3