1 2 Example of a Decision Tree al

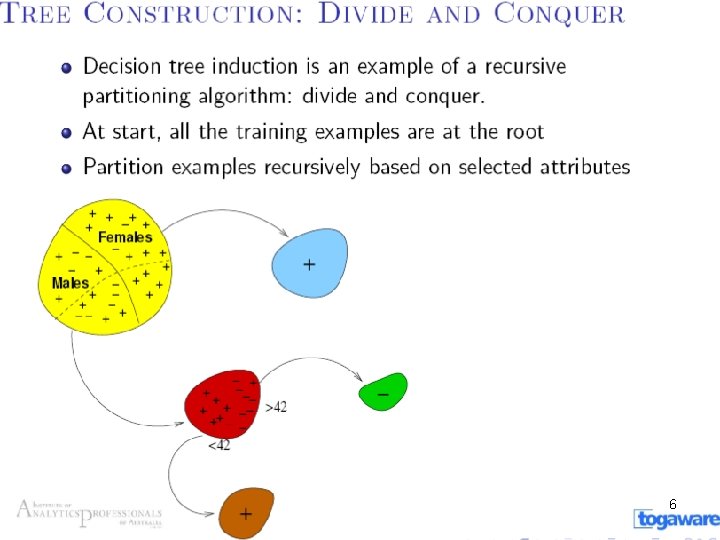

















- Slides: 35

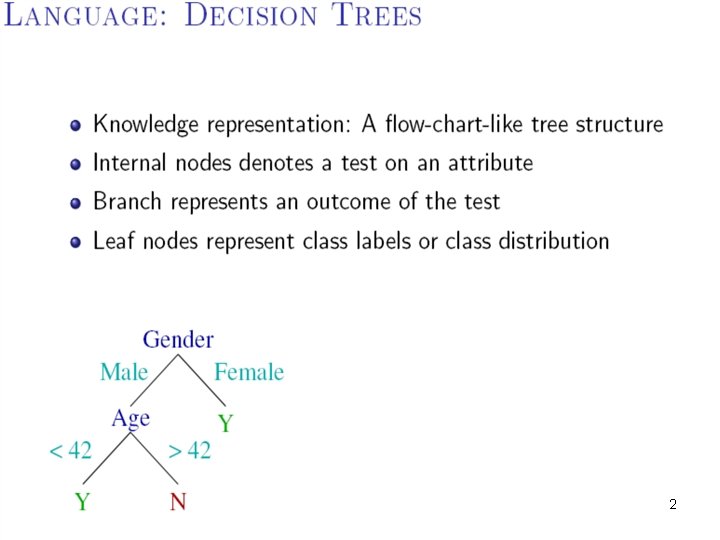
1

2

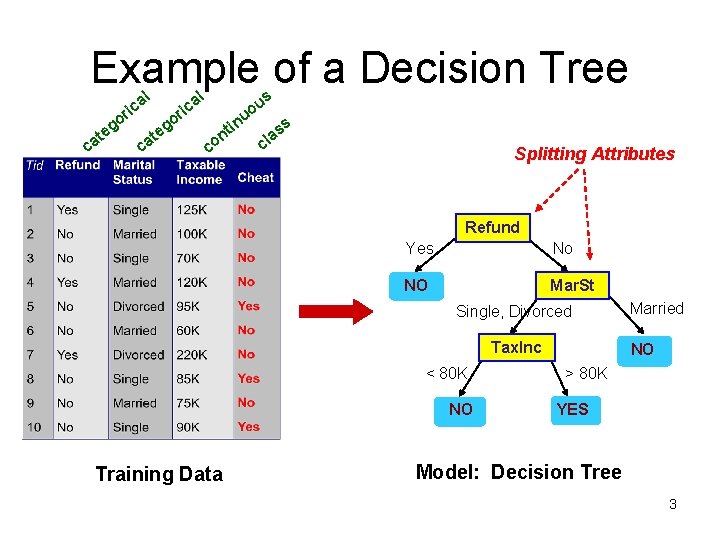
Example of a Decision Tree al ric c at o eg c at al o eg ric u s u o in nt co ss a cl Splitting Attributes Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Training Data Married NO > 80 K YES Model: Decision Tree 3

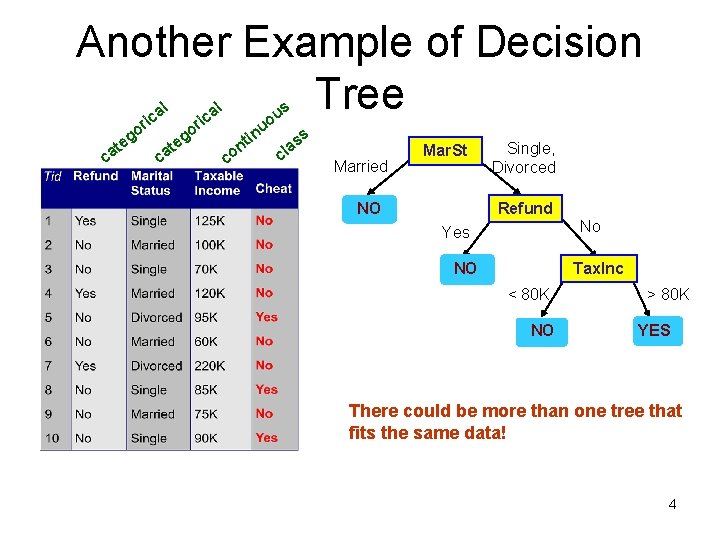
Another Example of Decision Tree l ca g te l a ric o o ca g te s a ric u uo co in t n ss a cl Married Mar. St NO Single, Divorced Refund No Yes NO Tax. Inc < 80 K NO > 80 K YES There could be more than one tree that fits the same data! 4

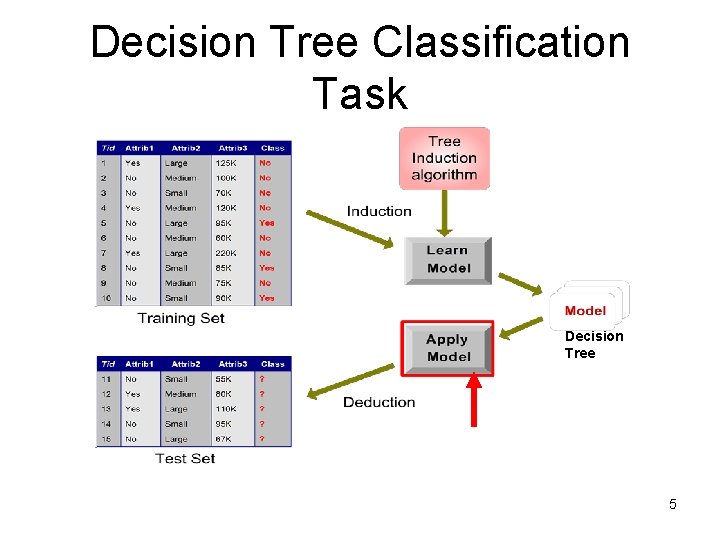
Decision Tree Classification Task Decision Tree 5

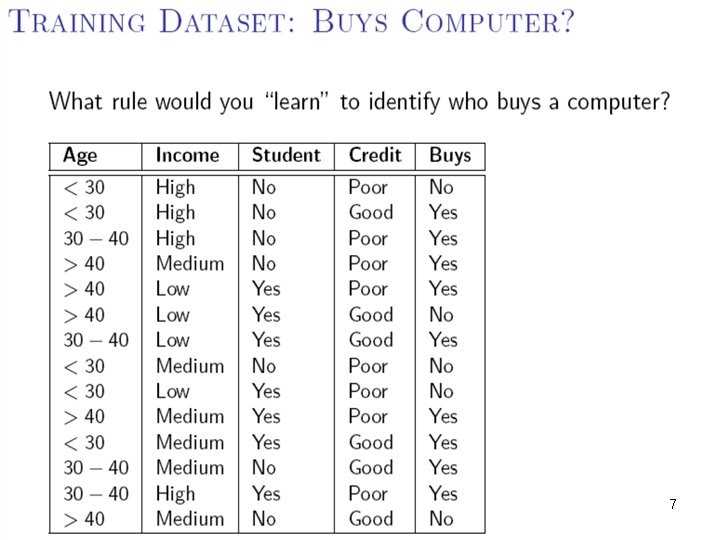
6

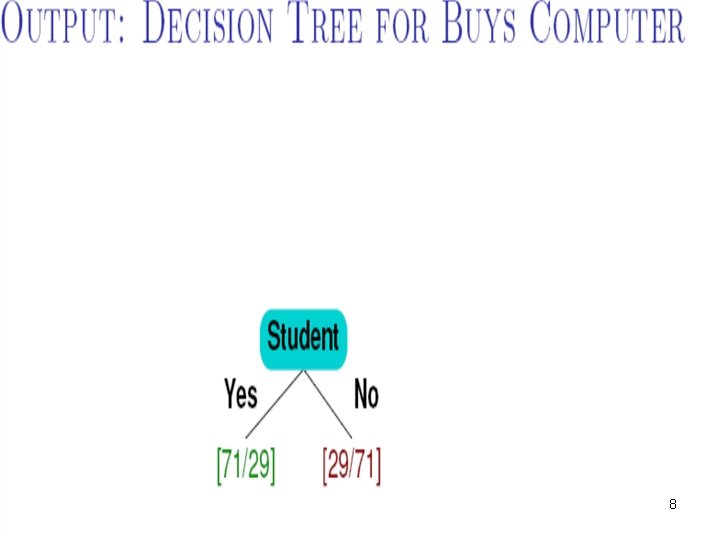
7

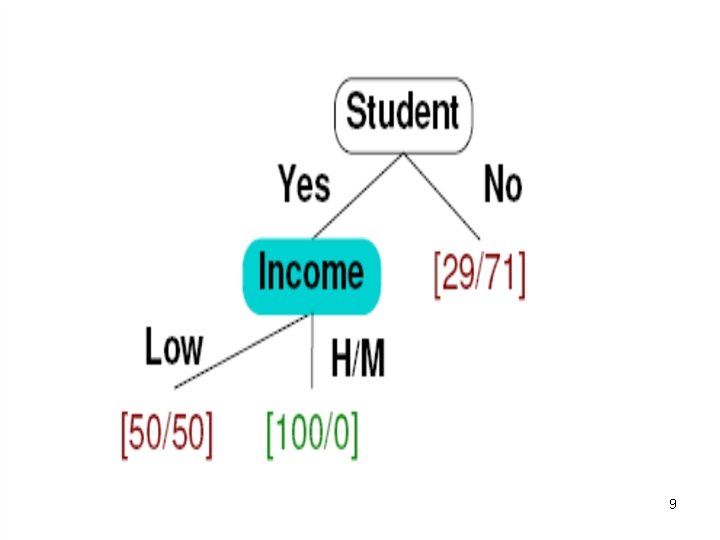
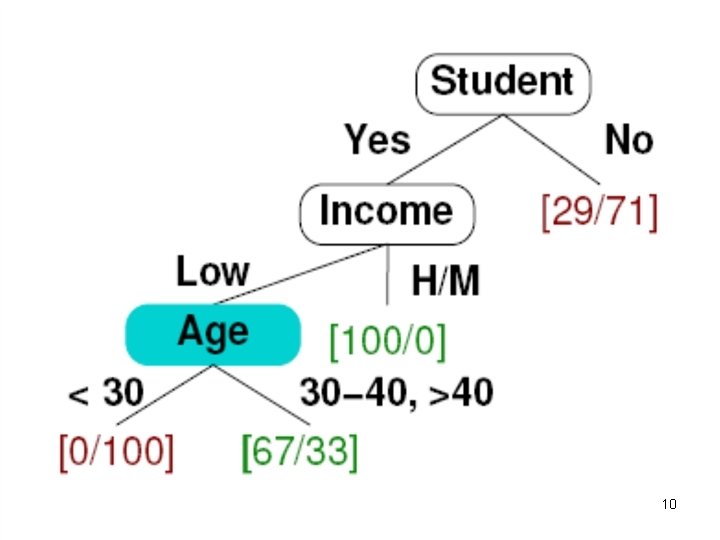
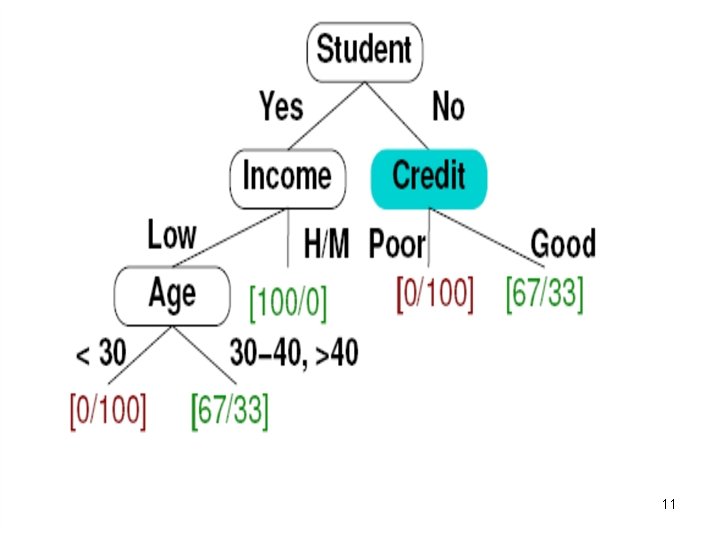
8

9

10

11

12

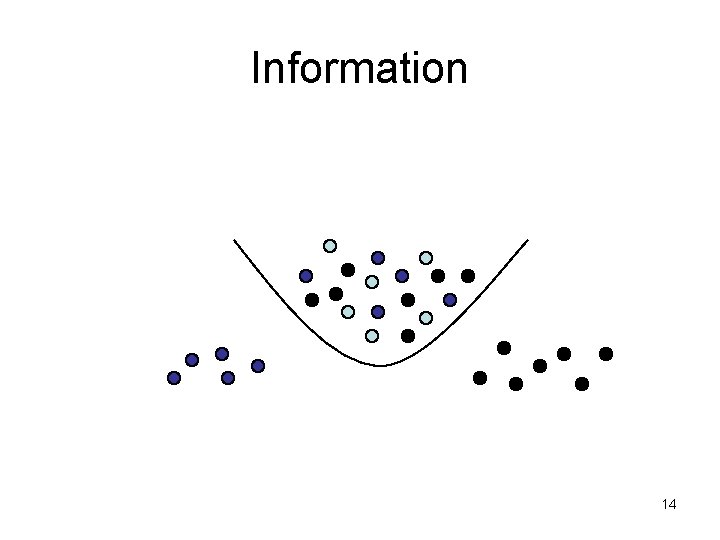
Decision Tree Induction is often based on Information Theory 13

Information 14

DT Induction • When all the marbles in the bowl are mixed up, little information is given. • When the marbles in the bowl are all from one class and those in the other two classes are on either side, more information is given. Use this approach with DT Induction ! 15

16

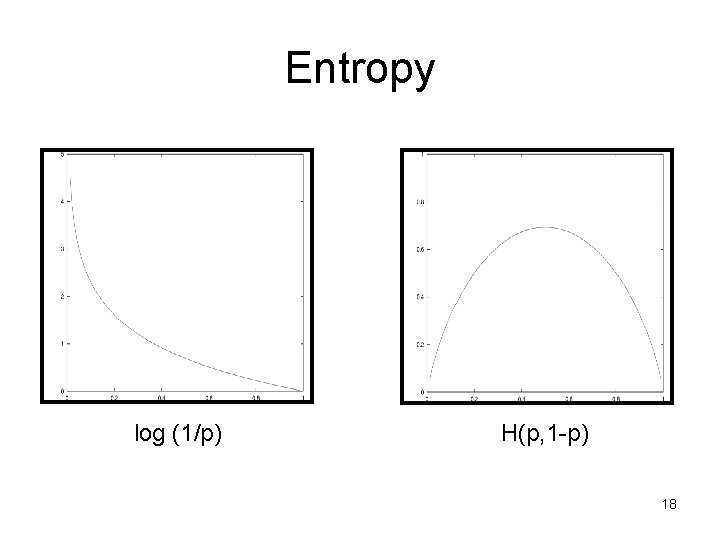
Information/Entropy • Given probabilitites p 1, p 2, . . , ps whose sum is 1, Entropy is defined as: • Entropy measures the amount of randomness or surprise or uncertainty. • Goal in classification – no surprise – entropy = 0 17

Entropy log (1/p) H(p, 1 -p) 18

19

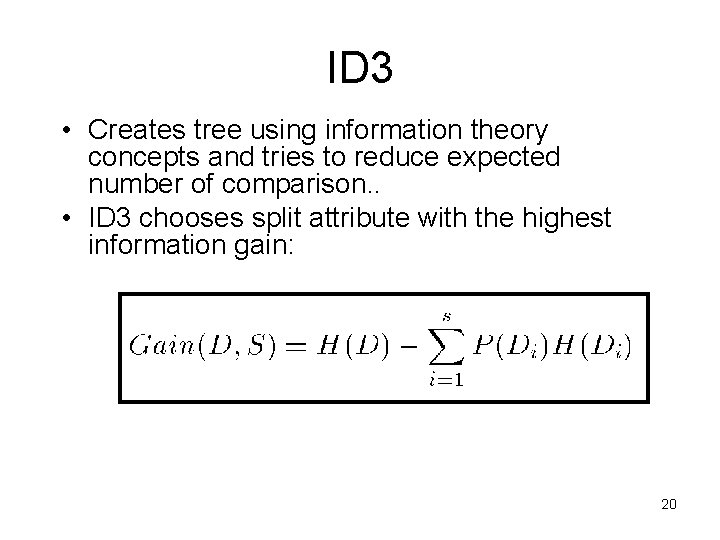
ID 3 • Creates tree using information theory concepts and tries to reduce expected number of comparison. . • ID 3 chooses split attribute with the highest information gain: 20

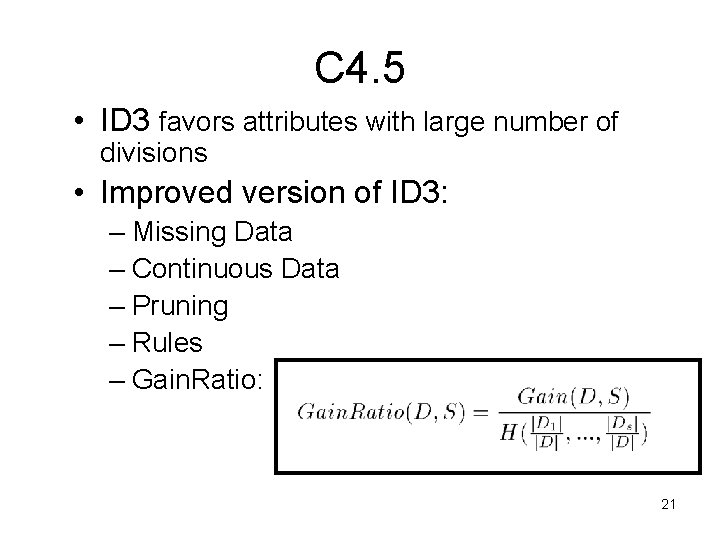
C 4. 5 • ID 3 favors attributes with large number of divisions • Improved version of ID 3: – Missing Data – Continuous Data – Pruning – Rules – Gain. Ratio: 21

CART • Create Binary Tree • Uses entropy • Formula to choose split point, s, for node t: • PL, PR : probability that a tuple in the training set will be on the left or right side of the tree. 22

Measure of Impurity: GINI • Gini Index for a given node t : (NOTE: p( j | t) is the relative frequency of class j at node t). – Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information – Minimum (0. 0) when all records belong to one class, implying most interesting information 23

Examples for computing GINI P(C 1) = 0/6 = 0 P(C 2) = 6/6 = 1 Gini = 1 – P(C 1)2 – P(C 2)2 = 1 – 0 – 1 = 0 P(C 1) = 1/6 P(C 2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0. 278 P(C 1) = 2/6 P(C 2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0. 444 24

Splitting Based on GINI • Used in CART, SLIQ, SPRINT. • When a node p is split into k partitions (children), the quality of split is computed as, where, ni = number of records at child i, n = number of records at node p. 25

Stopping Criteria for Tree Induction • Stop expanding a node when all the records belong to the same class • Stop expanding a node when all the records have similar attribute values • Early termination 26

Notes on Overfitting • Overfitting results in decision trees that are more complex than necessary • Training error no longer provides a good estimate of how well the tree will perform on previously unseen records • Need new ways for estimating errors 27

Estimating Generalization Errors • Re-substitution errors: error on training ( e(t) ) • Generalization errors: error on testing ( e’(t)) • Methods for estimating generalization errors: – Optimistic approach: e’(t) = e(t) – Pessimistic approach: • • • For each leaf node: e’(t) = (e(t)+0. 5) Total errors: e’(T) = e(T) + N 0. 5 (N: number of leaf nodes) For a tree with 30 leaf nodes and 10 errors on training (out of 1000 instances): Training error = 10/1000 = 1% Generalization error = (10 + 30 0. 5)/1000 = 2. 5% – Reduced error pruning (REP): • uses validation data set to estimate generalization error 28

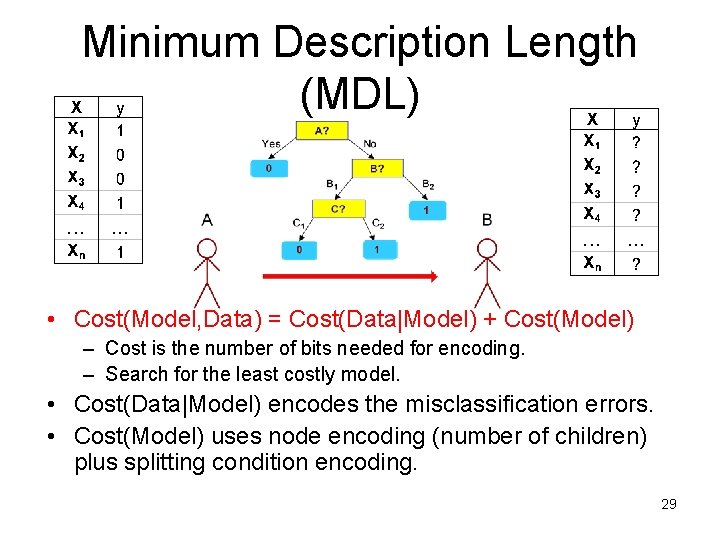
Minimum Description Length (MDL) • Cost(Model, Data) = Cost(Data|Model) + Cost(Model) – Cost is the number of bits needed for encoding. – Search for the least costly model. • Cost(Data|Model) encodes the misclassification errors. • Cost(Model) uses node encoding (number of children) plus splitting condition encoding. 29

How to Address Overfitting • Pre-Pruning (Early Stopping Rule) – Stop the algorithm before it becomes a fully-grown tree – Typical stopping conditions for a node: • Stop if all instances belong to the same class • Stop if all the attribute values are the same – More restrictive conditions: • Stop if number of instances is less than some user-specified threshold • Stop if expanding the current node does not improve impurity measures (e. g. , Gini or information gain) • … 30

How to Address Overfitting… • Post-pruning – Grow decision tree to its entirety – Trim the nodes of the decision tree in a bottom -up fashion – If generalization error improves after trimming, replace sub-tree by a leaf node. – Class label of leaf node is determined from majority class of instances in the sub-tree – Can use MDL for post-pruning 31

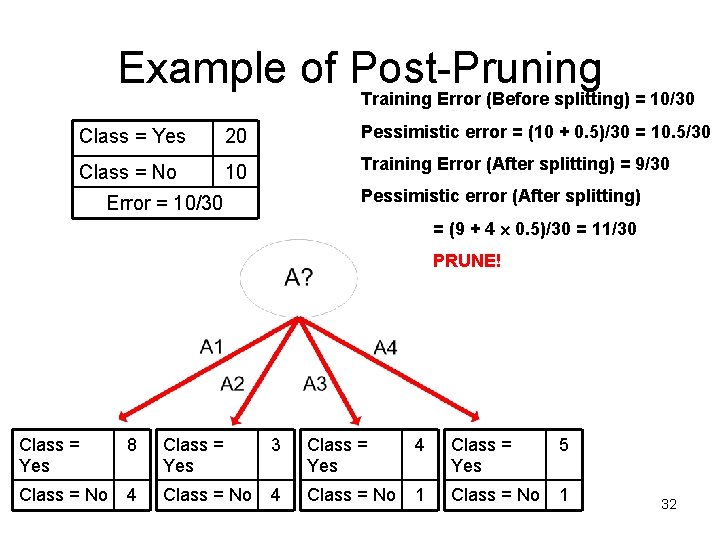
Example of Post-Pruning Training Error (Before splitting) = 10/30 Class = Yes 20 Pessimistic error = (10 + 0. 5)/30 = 10. 5/30 Class = No 10 Training Error (After splitting) = 9/30 Pessimistic error (After splitting) Error = 10/30 = (9 + 4 0. 5)/30 = 11/30 PRUNE! Class = Yes 8 Class = Yes 3 Class = Yes 4 Class = Yes 5 Class = No 4 Class = No 1 32

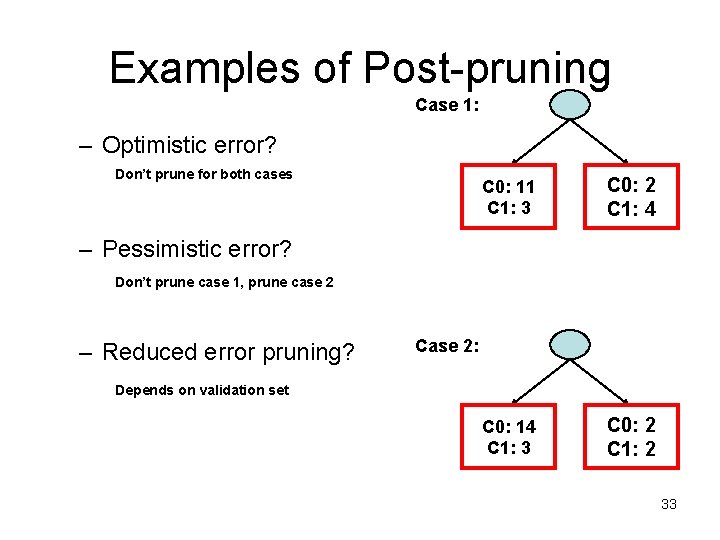
Examples of Post-pruning Case 1: – Optimistic error? Don’t prune for both cases C 0: 11 C 1: 3 C 0: 2 C 1: 4 C 0: 14 C 1: 3 C 0: 2 C 1: 2 – Pessimistic error? Don’t prune case 1, prune case 2 – Reduced error pruning? Case 2: Depends on validation set 33

34

35