1 2 Displaying and Describing Categorical Quantitative Data

1. 2 Displaying and Describing Categorical & Quantitative Data

You should be able to: • Recognize when a variable is categorical or quantitative • Choose an appropriate display for a categorical variable and a quantitative variable • Summarize the distribution with a bar, pie chart, stemleaf plot, histogram, dot plot, box plots • Know how to make a contingency table • Describe the distribution of categorical variables in terms of relative frequencies • Be able to describe the distribution of quantitative variables in terms of its shape, center and spread • Describe abnormalities or extraordinary features of distribution • Discuss outliers and how they deviate from the overall pattern

3 RULES of EXPLORATORY DATA ANALYSIS 1. MAKE A PICTURE – find patterns in difficult to see from a chart 2. MAKE A PICTURE – show important features in graph 3. MAKE A PICTURE- communicates your data to others

Concepts to know! • • • Bar graph Histogram Dot plot Stem leaf plot Scatterplots Boxplots

Which graph to use? • Depends on type of data • Depends on what you want to illustrate

Categorical Data • The objects being studied are grouped into categories based on some qualitative trait. • The resulting data are merely labels or categories.
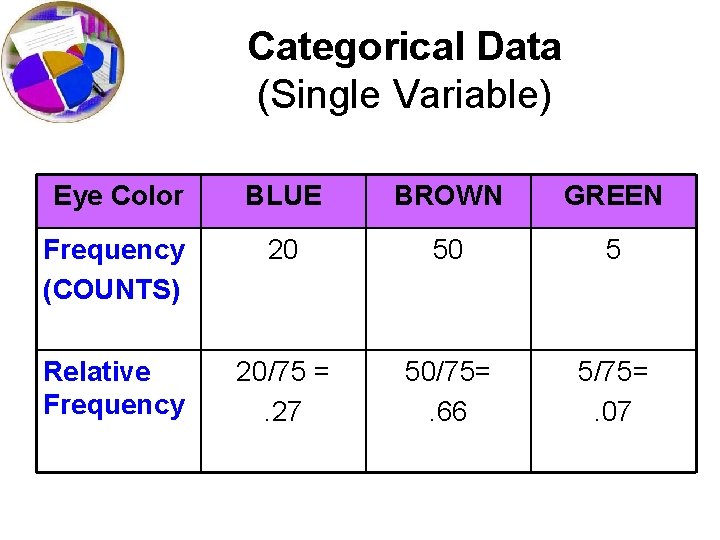
Categorical Data (Single Variable) Eye Color BLUE BROWN GREEN Frequency (COUNTS) 20 50 5 Relative Frequency 20/75 =. 27 50/75=. 66 5/75=. 07
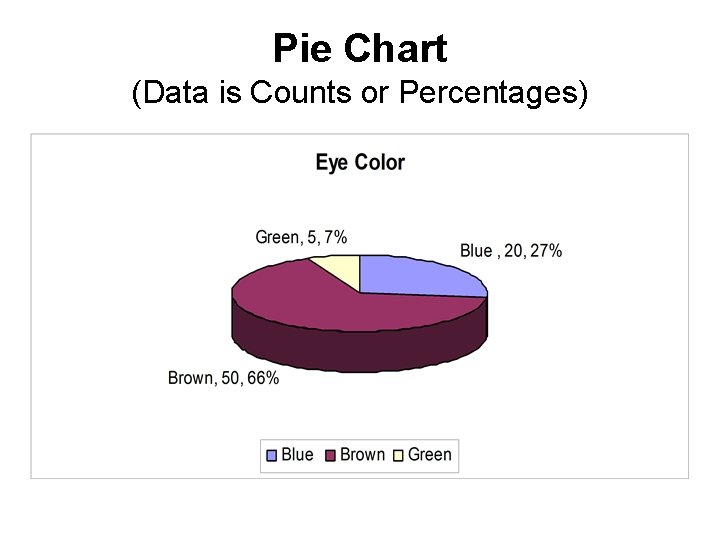
Pie Chart (Data is Counts or Percentages)
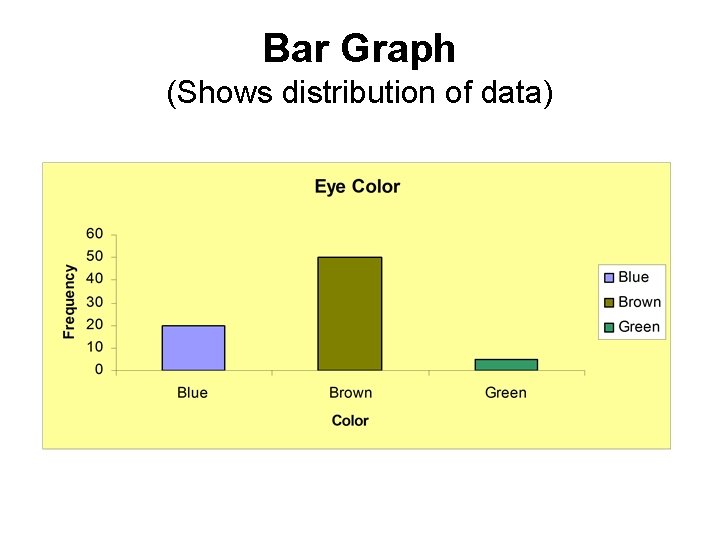
Bar Graph (Shows distribution of data)

Bar Graph • Summarizes categorical data. • Horizontal axis represents categories, while vertical axis represents either counts (“frequencies”) or percentages (“relative frequencies”). • Used to illustrate the differences in percentages (or counts) between categories.
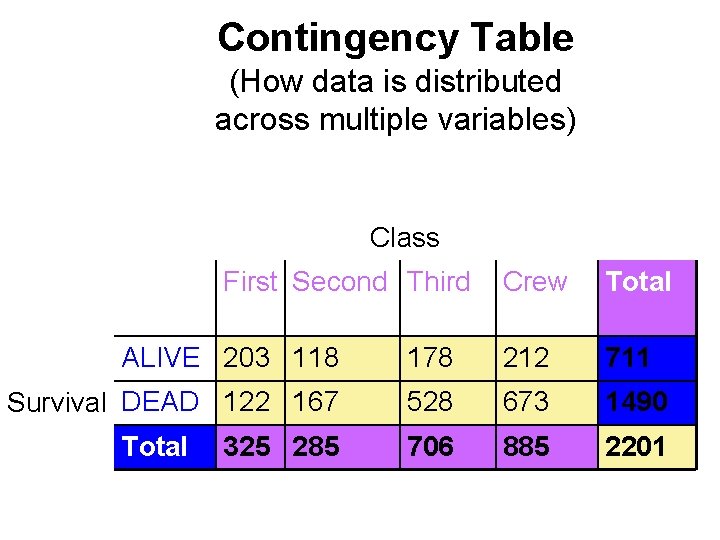
Contingency Table (How data is distributed across multiple variables) Class First Second Third Crew Total ALIVE 203 118 178 212 711 Survival DEAD 122 167 528 673 1490 706 885 2201 Total 325 285

What can go wrong when working with categorical data? • Pay attention to the variables and what the percentages represent (9. 4% of passengers who were in first class survived is different from 67% of survivors were first class passengers!!!) • Make sure you have a reasonably large data set (67% of the rats tested died and 1 lived)

Analogy Bar chart is to categorical data as histogram is to. . . quantitative data.
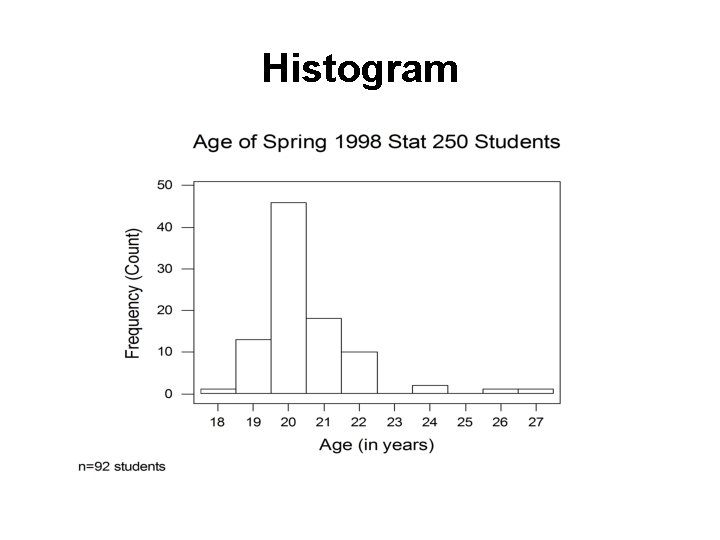
Histogram

Histogram • Divide measurement up into equal-sized categories (BIN WIDTH) • Determine number (or percentage) of measurements falling into each category. • Draw a bar for each category so bars’ heights represent number (or percent) falling into the categories. • Label and title appropriately. • http: //www. stat. sc. edu/~west/javahtml/Histogram. html

Histogram Use common sense in determining number of categories to use. Between 6 & 15 intervals is preferable (Trial-and-error works fine, too. )
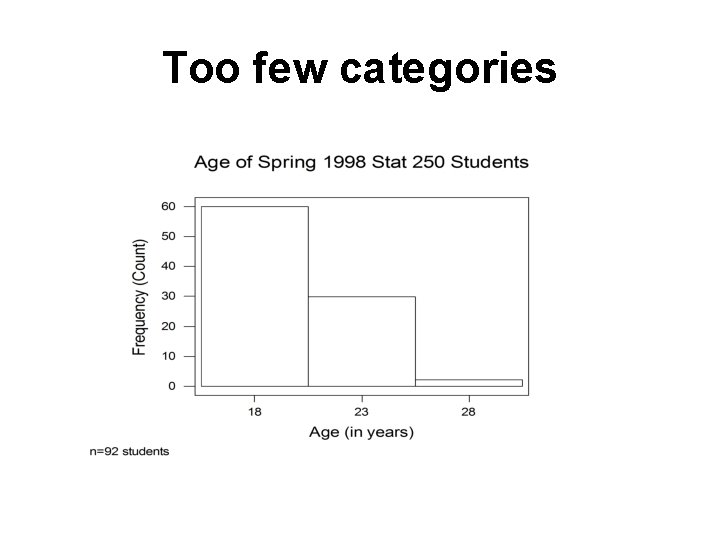
Too few categories
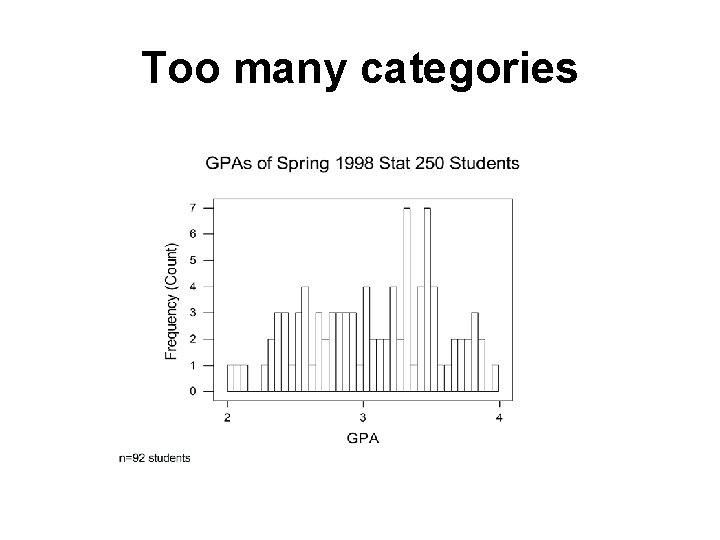
Too many categories
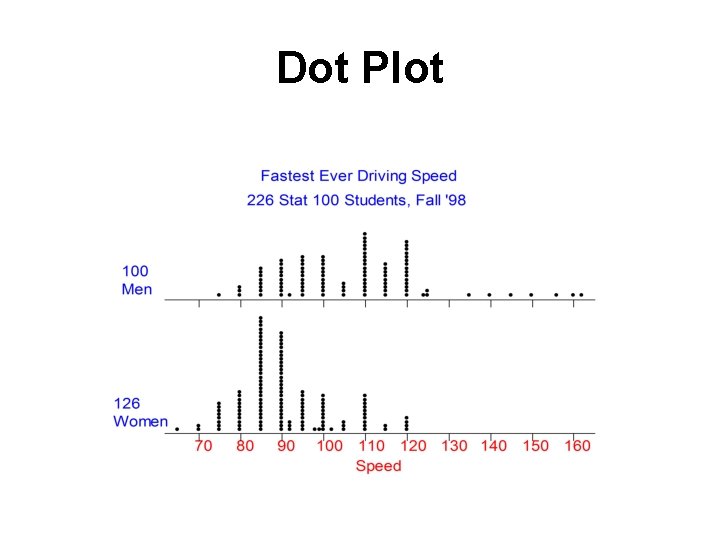
Dot Plot

Dot Plot • Summarizes quantitative data. • Horizontal axis represents measurement scale. • Plot one dot for each data point.

Stem-and-Leaf Plot Stem-and-leaf of Shoes N = 139 Leaf Unit = 1. 0 12 0 223334444444 63 0 5555555666667777777888888899999 (33) 1 00000001111222223333444 43 1 55556667777888 25 2 00000023 12 2 5557 8 3 0023 4 4 00 2 4 2 5 0 1 5 1 6 1 7 5

Stem-and-Leaf Plot • Summarizes quantitative data. • Each data point is broken down into a “stem” and a “leaf. ” • First, “stems” are aligned in a column. • Then, “leaves” are attached to the stems.

Box Plot

Box Plot • Summarizes quantitative data. • Vertical (or horizontal) axis represents measurement scale. • Lines in box represent the 25 th percentile (“first quartile”), the 50 th percentile (“median”), and the 75 th percentile (“third quartile”), respectively.

5 Number Summary • • • Minimum Q 1 (25 th percentile) Median (50 th percentile) Q 3 (75 th percentile) Maximum

An aside. . . • Roughly speaking: – The “ 25 th percentile” is the number such that 25% of the data points fall below the number. – The “median” or “ 50 th percentile” is the number such that half of the data points fall below the number. – The “ 75 th percentile” is the number such that 75% of the data points fall below the number.

Box Plot (cont’d) • “Outliers” are drawn to the most extreme data points that are not more than 1. 5 times the length of the box beyond either quartile(IQR). IQR = Q 3 - Q 1 Outliers(upper) > Q 3+1. 5 * IQR Outliers(lower)<Q 1 -1. 5*IQR
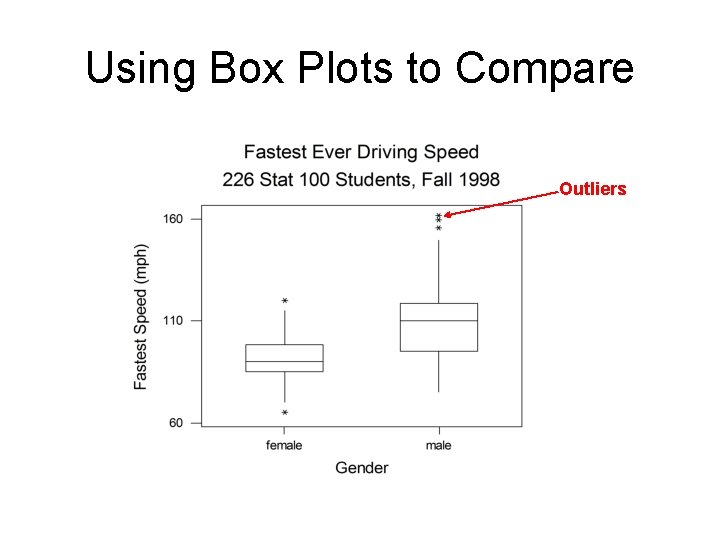
Using Box Plots to Compare Outliers

Strengths and Weaknesses of Graphs for Quantitative Data • Histograms – Uses intervals – Good to judge the “shape” of a data – Not good for small data sets • Stem-Leaf Plots – Good for sorting data (find the median) – Not good for large data sets

Strengths and Weaknesses of Graphs for Quantitative Data • Dotplots – Uses individual data points – Good to show general descriptions of center and variation – Not good for judging shape for large data sets • Boxplots – Good for showing exact look at center, spread and outliers – Not good for judging shape

Analogy Contingency table is to categorical data with two variables as scatterplot is to. . quantitative data with two variables.
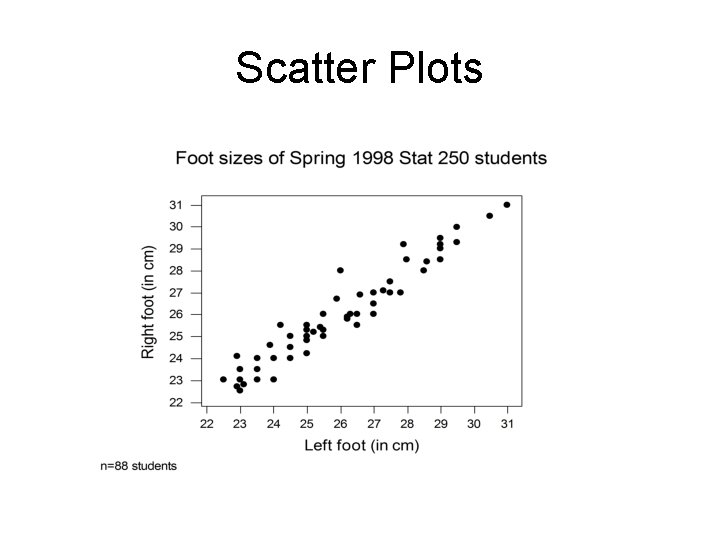
Scatter Plots

Scatter Plots • Summarizes the relationship between two quantitative variables. • Horizontal axis represents one variable and vertical axis represents second variable. • Plot one point for each pair of measurements.
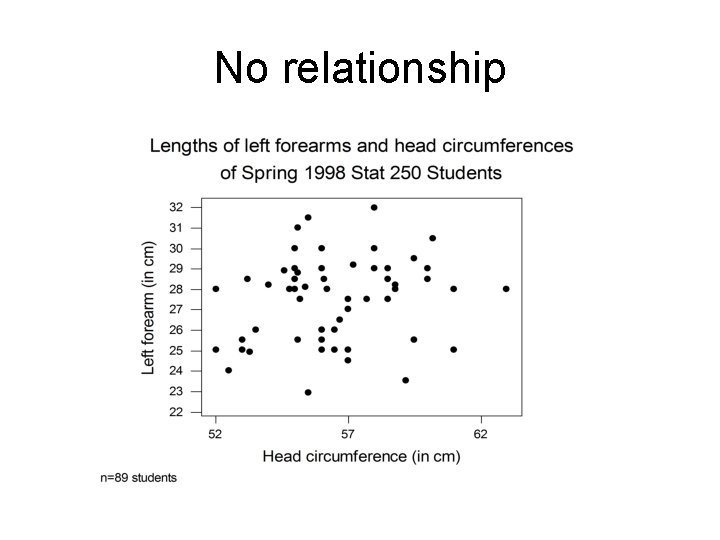
No relationship

Summary • Many possible types of graphs. • Use common sense in reading graphs. • When creating graphs, don’t summarize your data too much or too little. • When creating graphs, label everything for others. Remember you are trying to communicate something to others!
GRAPHICAL ANALYSIS

• CENTER • SPREAD
Graphical Analysis Center (Location) Spread (Variation) Shape

Interesting Features Identified by Graphs • • Center (Location) Spread (Variability) Shape Individual Values Compare Groups Identify Outliers LOOK FOR PATTERNS, CLUSTERS, GAPS!!!!! LOOK FOR DEVIATIONS FROM THE GENERAL PATTERN!!!!! http: //bcs. whfreeman. com/bps 3 e/
Shape of Graph

Shape of Graph • Symmetry-Skewness • Modes(peaks)

SYMMETRY & SKEWNESS • Skewness - a measure of symmetry, or more precisely, the lack of symmetry. • A distribution, or data set, is symmetric if it looks the same to the left and right of the center point.

Kurtosis • Kurtosis - a measure of whether the data are peaked or flat relative to a normal distribution. • High kurtosis tend to have a distinct peak near the mean, decline rather rapidly, and have heavy tails. L • Low kurtosis tend to have a flat top near the mean rather than a sharp peak.
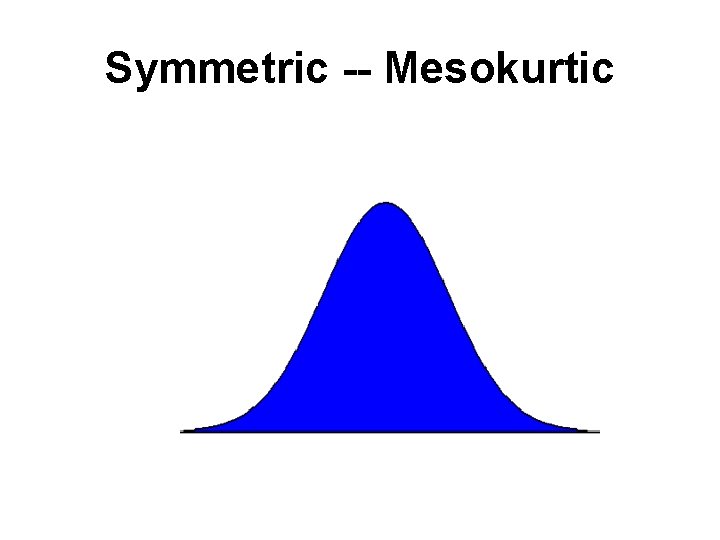
Symmetric -- Mesokurtic

Symmetric -- Platykurtic
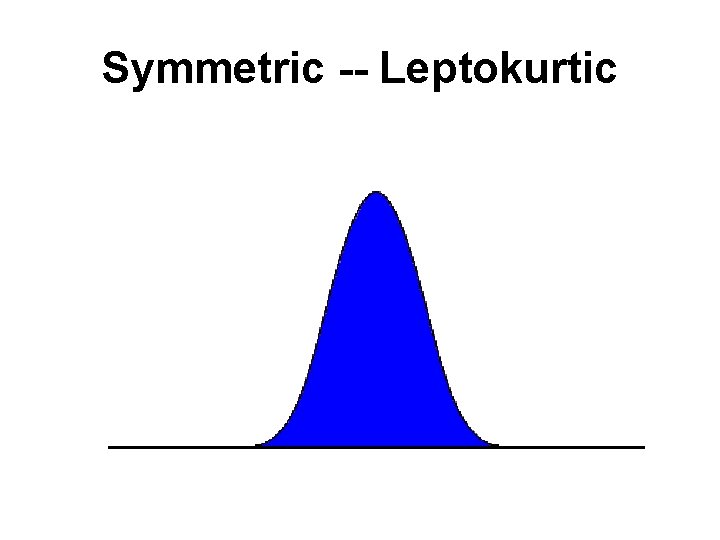
Symmetric -- Leptokurtic
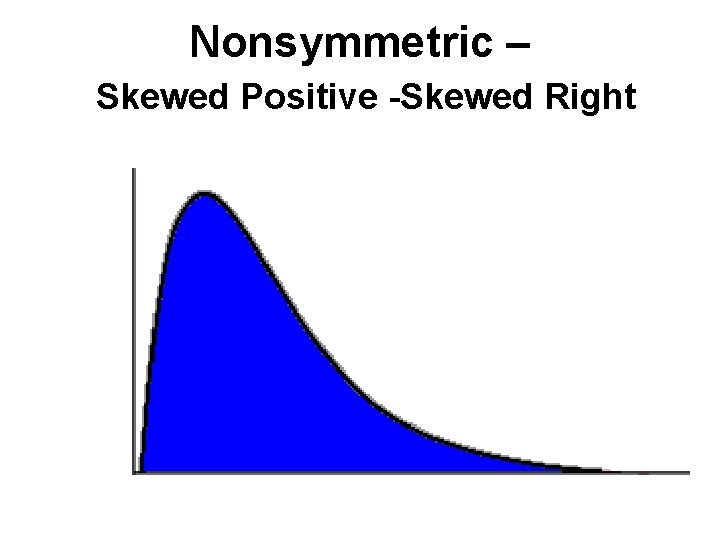
Nonsymmetric – Skewed Positive -Skewed Right

Nonsymmetric – Skewed Negative -- Skewed Left
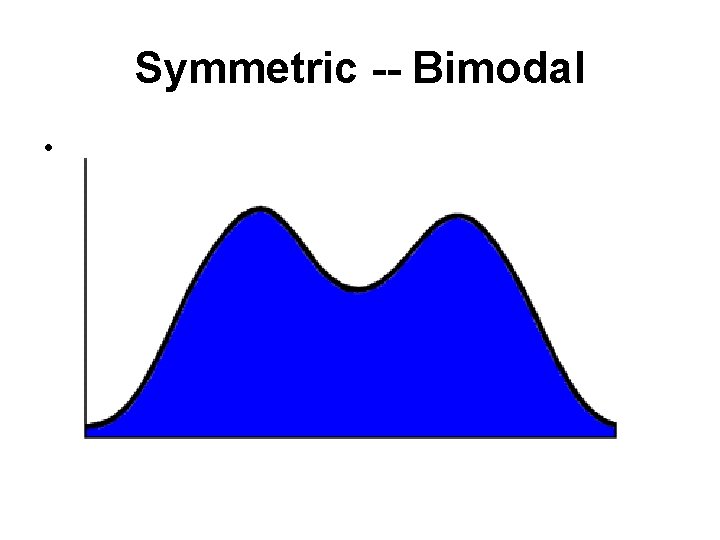
Symmetric -- Bimodal •

Describing Distributions – SOCS Rock! • Shape • Outliers • Center • Spread
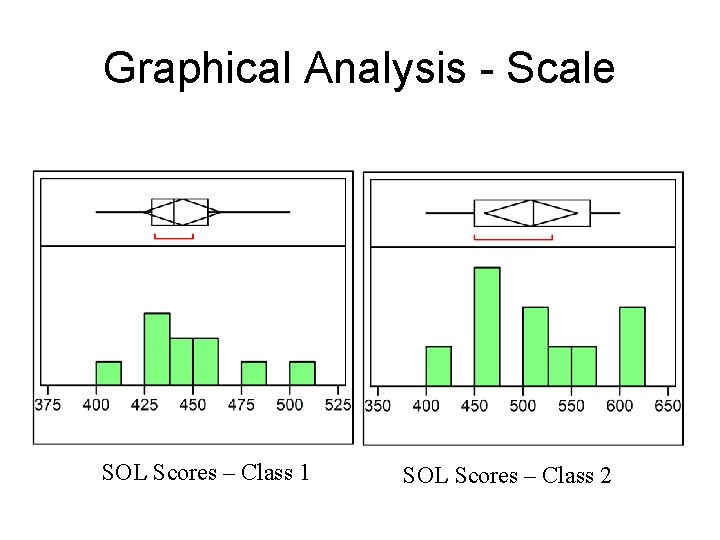
Graphical Analysis - Scale SOL Scores – Class 1 SOL Scores – Class 2

Graphical Analysis - Scale SOL Scores – Class 1 SOL Scores – Class 2

SOL Scores – Class 1 SOL Scores – Class 2

• Comparing Histograms
- Slides: 54