1 2 Algebra The Language of Algebra Why

1. 2 Algebra The Language of Algebra

Why Algebra is good. . . It involves • • • Logic Being systematic Problem Solving Reasoning Thinking Skills Selecting the best tool for the problem • • Organising your working Being careful and accurate Reasoning Working in a step-by-step way All very useful skills to develop
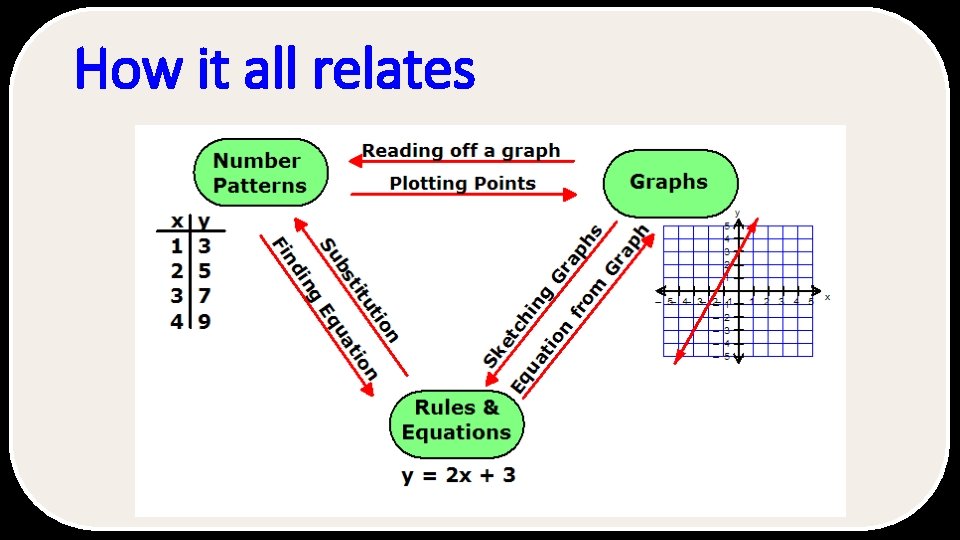
How it all relates

The Language of Algebra uses a lot of everyday common words. Our objective is to be able to write an algebraic expression for a word phrase or write a word phrase for an expression. Note: an expression is a mathematical phrase that can contain ordinary numbers, variables (like x or y), and operators (like add, subtract, divide and multiply)

The Language of Algebra In algebra letters are used to represent any possible number eg pocket $ (p) = $5 x time worked (t) p = 5 t These are called VARIABLES x, y, z are frequently used Normally variables are lower case Numbers are CONSTANTS (if alone) e. g. 3 + 4 x – 5 + 7 x = 14 or COEFFICIENTS (if in front of variables) e. g. 4 x A TERM is a constant or coefficient and variable +12 4 x + 8 y – 6 + 2 x + 12 y

The Language of Algebra An equation must have an “=” e. g. 4 x + 7 = 11 or 3(x – 5)(x + 4) = 12 x – 5 An expression is simply an equation with the “=“ part e. g. 4 x + 7 The solution of an equation is the number(s) which can be substituted in place of the variable “x” to make the equation true.

The Language of Algebraic terms have numbers and variables that are sometimes raised to an exponent Exponent is 3 Coefficient is 8 Variable is x

Although they are closely related, a Great Dane weighs about 40 times as much as a Chihuahua. An expression for the weight of the Great Dane could be 40 c, where c is the weight of the Chihuahua. When solving real-world problems, you will need to translate words, or verbal expressions, into algebraic expressions.

In order to translate a word phrase into an algebraic expression, we must first know some key word phrases for the basic operations.
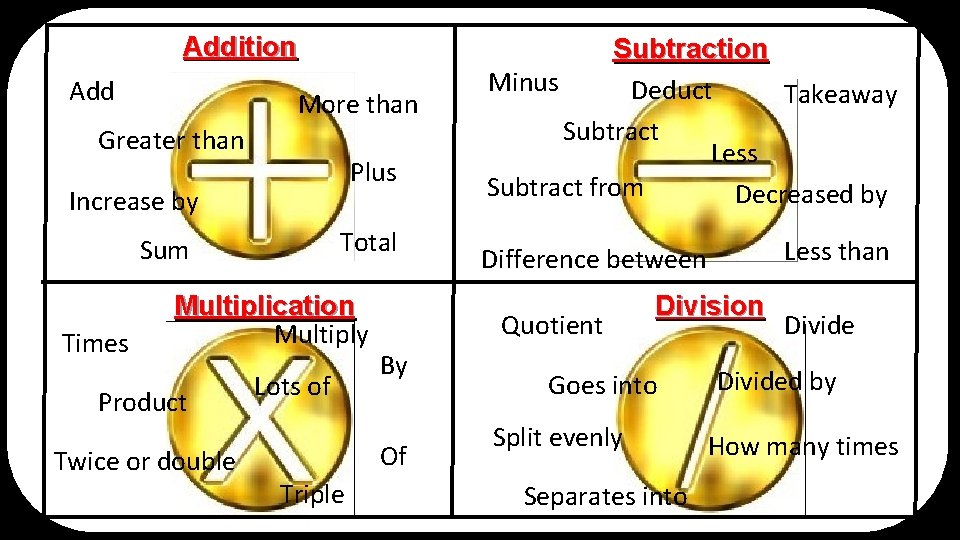
Addition Add More than Greater than Plus Increase by Total Sum Times Multiplication Multiply Product Twice or double Lots of By Less than Difference between Quotient Of Triple Subtraction Minus Deduct Takeaway Subtract Less Subtract from Decreased by Division Goes into Split evenly Separates into Divided by How many times

Some examples Addition Subtraction • 3 more than x • 7 minus 3 • the sum of 10 and a number c • a number decreased by 4 • a number n increased by 4 • the difference between 10 and a number y • 5 plus 8 plus x • 6 less than the number z Multiplication Division • twice the number x • 12 divided by the number x • 4. 2 times a number e • the quotient of 25 and a number b • the product of 3 and a number t • 4 split evenly into the number e • 4 lots of the number x • 10 divide g

Some points to note: • Multiplication expressions should be written in side-by-side form, with the number always in front of the variable. e. g. 3 a 2 t 1. 5 c 0. 4 f • Division expressions should be written using the fraction bar instead of the traditional division sign. e. g. • Numbers should always be written before variables, and variables should be in alphabetical order e. g. 4 x not x 4 3 ab not 3 ba

Some examples: a) converting f metres into millimetres b) a car travels at 75 kph for h hours c) the area of a rectangle with a length of 10 and a width of w d) Converting x millimetres into metres e) the cost for tickets if you purchase 5 adult tickets at x dollars each f) the cost for tickets if you purchase 3 children’s tickets at y dollars each g) the total cost for 5 adult tickets and 3 children’s tickets using the dollar amounts from the previous two problems (problems e and f)

Order of Operations for Algebraic Expressions Before we can evaluate an expression we need to know the order in which the operations are done. For all numerical or algebraic expressions, the order of evaluation is (BEDMAS): B rackets and Parentheses (inner most ones first) E xponent D ivision M ultiplication A ddition S ubtraction First priority Second priority Third priority Fourth priority If an expression involves two or more operations at the same level of priority, those operations are done from left to right.

Some examples: 1. 10 – 5 x 6 – 8 ÷ 4 = 2. 2 + 4 ÷ 2 + 4 = -22 8 3. 5 + 10 + 7 ÷ (– 7) = 14 4. 2 + 10 ÷ (10 – 5) = 4 5. 4 + 9[3 + 8(4 – 7) + 10] = -95 6. 4 – 3[4 – 2(6 – 3)] ÷ 2 = 7 7. 16 – 3(8 – 3)2 ÷ 5 = 1 8. 14 x + 5[6 – (2 x + 3)] = 4 x + 15
- Slides: 15