1 2 A Stretches 1 The graph of

1. 2 A Stretches 1. The graph of y + 3 = f(x) up 3 units is the graph of f(x) translated… left 3 units x down 3 units right 3 units 2. The graph of f(x) + 4 is the graph of f(x) translated… x 4 units up 4 units left 4 units down 4 units right 3. The graph of f(x – 7) + 6 is the graph of f(x) that has been translated. . 7 units left, 6 units up 7 units left, 6 units down 7 units right, 6 units down x 7 units right, 6 units up 4. In general, the graph of f(x – h) + k, where h and k are positive, as compared to the parent function graph f(x), is translated h units left and k units up h units left and k units down x h units right and k units up 30 -1 right and k units down Math h units 1

Investigating Vertical Stretches: Recall the affect of “a” for a Quadratic Math 30 -1 2

Vertical Stretches: The effect of parameter a. A stretch changes the shape of the graph. (Translations changed the position of a graph. ) Function Transformations: Vertical Stretch |a| describes a vertical stretch about the x-axis. An Invariant point is a point on a graph that remains unchanged after a transformation. 1. 2 A Vertical Stretches Math 30 -1 3

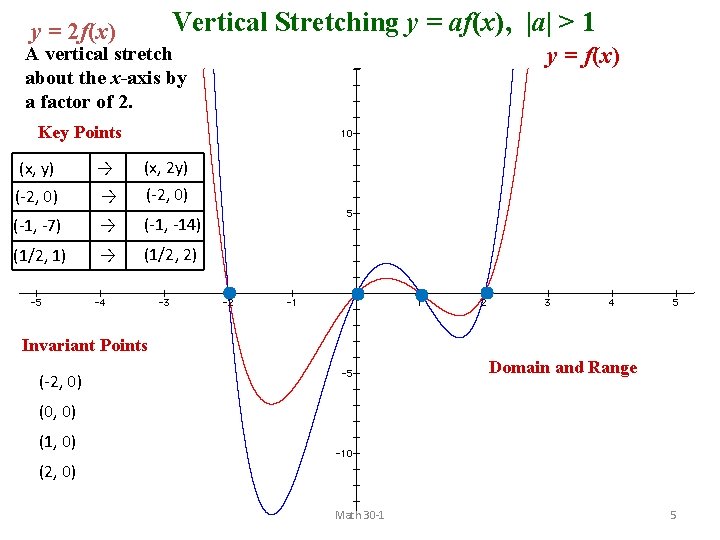
Vertical Stretches In general, for any function y = f(x), the graph of the function y =a f(x) has been vertically stretched about the x-axis by a factor of |a|. The point (x, y) → (x, ay). Only the y coordinates are affected. Invariant points are on the line of stretch, the x-axis. are the x-intercepts. When |a| > 1, the points on the graph move farther away from the x-axis. Vertical stretch by a factor of 3 When |a|< 1, the points on the graph move closer to the x-axis. Vertical stretch by a factor of ⅓ Math 30 -1 4

Vertical Stretching y = af(x), |a| > 1 y = 2 f(x) y = f(x) A vertical stretch about the x-axis by a factor of 2. Key Points (x, y) → (x, 2 y) (-2, 0) → (-2, 0) (-1, -7) → (-1, -14) (1/2, 1) → (1/2, 2) Invariant Points Domain and Range (-2, 0) (0, 0) (1, 0) (2, 0) Math 30 -1 5

Vertical Stretches about the x-axis y = af(x), |a| < 1 Consider Write the equation of the function after a vertical stretch about the x-axis by a factor of ½. Write the transformation in function notation. Write the coordinates of the image of the point (-7, 7) (-7, 3. 5) The point (x, y) maps to List any invariant points. How are the domain and range affected? Math 30 -1 6

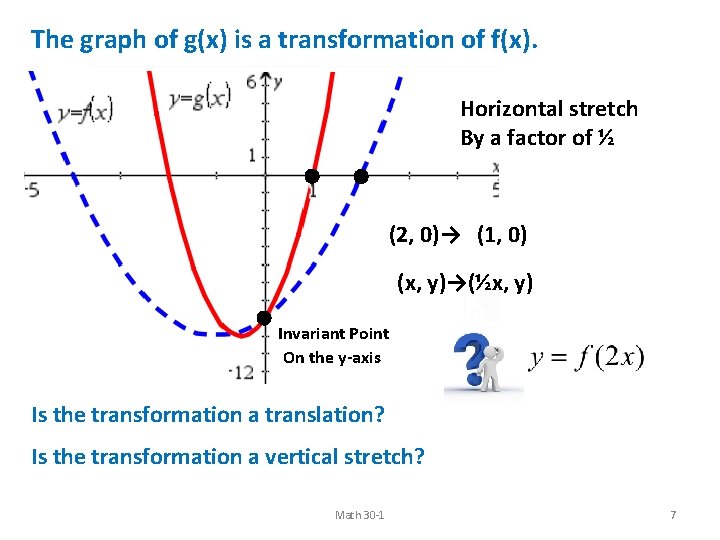
The graph of g(x) is a transformation of f(x). Horizontal stretch By a factor of ½ (2, 0)→ (1, 0) (x, y)→(½x, y) Invariant Point On the y-axis Is the transformation a translation? Is the transformation a vertical stretch? Math 30 -1 7

Horizontal Stretches In general, for any function y = f(x), the graph of the function y = f(bx) has been horizontally stretched by a factor of The point (x, y) → . Only the x coordinates are affected. Invariant points are on the line of stretch, the y-axis. are the y-intercepts. When |b| > 1, the points on the graph move closer to the y-axis. Horizontal stretch by a factor of ⅓ When |b|< 1, the points on the graph move farther away from the x-axis. Horizontal stretch by a factor of 4 Math 30 -1 8

Characteristics of Horizontal Stretches about the y-axis Consider Write the equation of the function after a horizontal stretch about the y-axis by a factor of 3. Write the transformation in function notation. Can it be written in any other way? Write the coordinates of the image of the point (-3, 3 ) → (-9, 3) Write the coordinates of the image of the point (x, y) List any invariant points. How are the domain and range affected? Math 30 -1 9

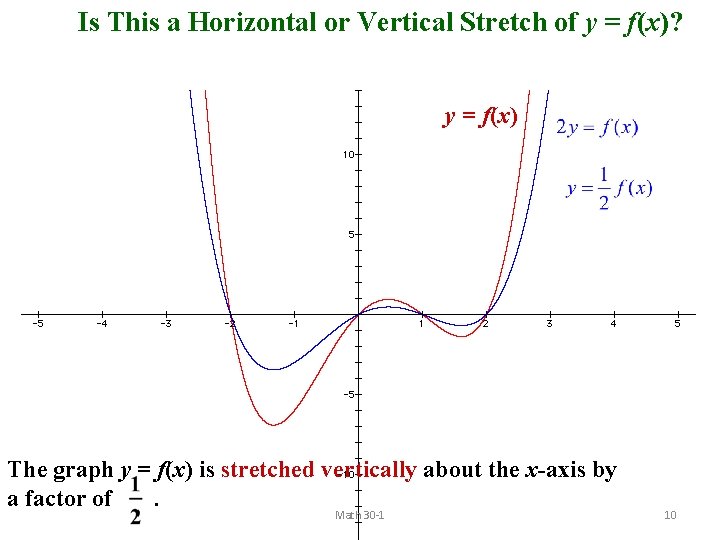
Is This a Horizontal or Vertical Stretch of y = f(x)? y = f(x) The graph y = f(x) is stretched vertically about the x-axis by a factor of. Math 30 -1 10

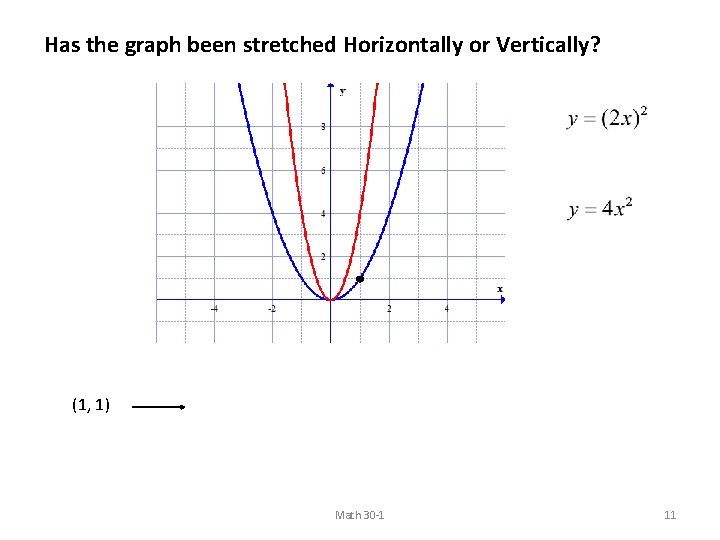
Has the graph been stretched Horizontally or Vertically? (1, 1) Math 30 -1 11

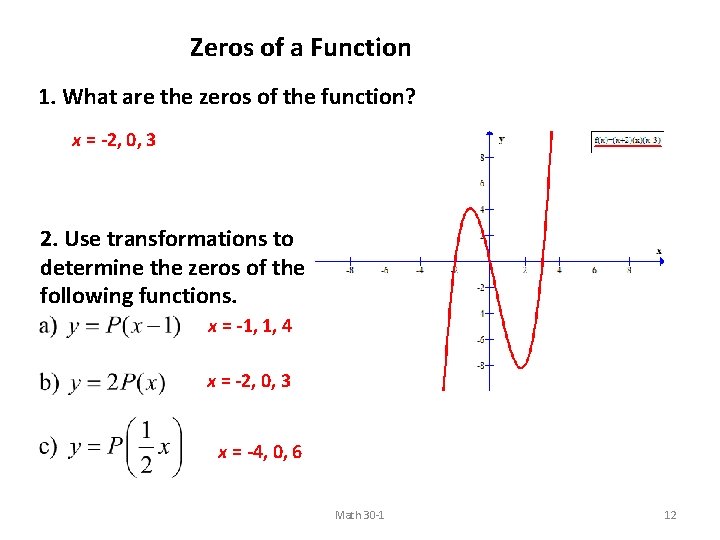
Zeros of a Function 1. What are the zeros of the function? x = -2, 0, 3 2. Use transformations to determine the zeros of the following functions. x = -1, 1, 4 x = -2, 0, 3 x = -4, 0, 6 Math 30 -1 12

Describing the Horizontal or Vertical Stretch of a Function Describe the transformation in words compared to the graph of a function y = f(x). a) y = f(3 x) b) 3 y = f(x) Stretch vertically by a factor Stretched horizontally by a factor of about the y-axis. c) y = f( of x) about the x-axis. d) y = 2 f(x) Stretched horizontally by a factor of 2 about the y-axis. Stretched vertically by a factor of Math 30 -1 about the x-axis. 13

Consider the graph of a function y = f(x) The transformation described by y = f(2 x+4) is horizontal stretch about the y-axis by a factor of ½. The translation described by y = f(2 x + 4) is horizontal shift of 4 units to the left. y = f(2(x + 2)) Translations must be factored Math 30 -1 14

Stating the Equation of y = af(kx) The graph of the function y = f(x) is transformed as described. Write the new equation in the form y = af(bx). a) Stretched horizontal by a factor of one-third about the y-axis, and stretched vertically about the x-axis by a factor of two. y = 2 f(3 x) b) Stretched horizontally by a factor of two about the y-axis and translated four units to the left. Math 30 -1 15

Assignment Page 28 2, 5 a, b, 6, 7 a, c, 8, 13, 14 c, d Math 30 -1 16

Check Write the equation of the function after a horizontal stretch about the y-axis by a factor of 3. Verify by substitution Math 30 -1 17