1 2 3 Adders Used to perform addition

1

2

3

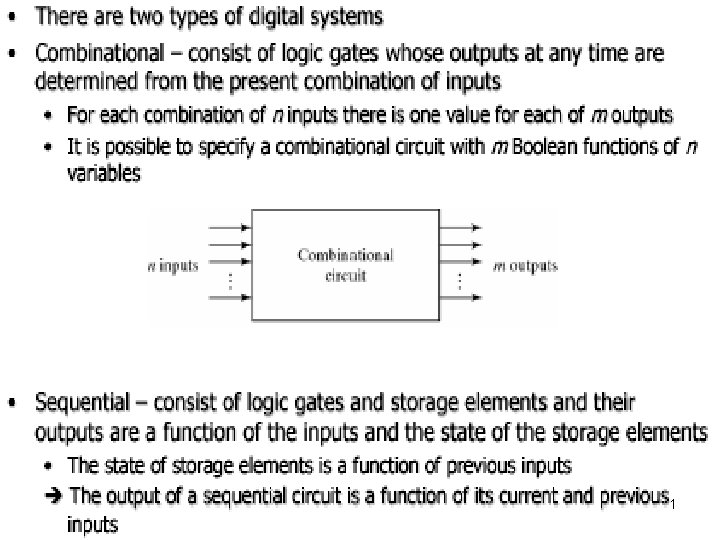
Adders • Used to perform addition, subtraction, multiplication, and division (sometimes) • Half-adder adds rightmost (least significant) bit • Full-adder adds all other bits, since a 1 may be carried into it. Use carry-out from one adder as the carry-in for the next adder • Combinational circuit (no memory) 4

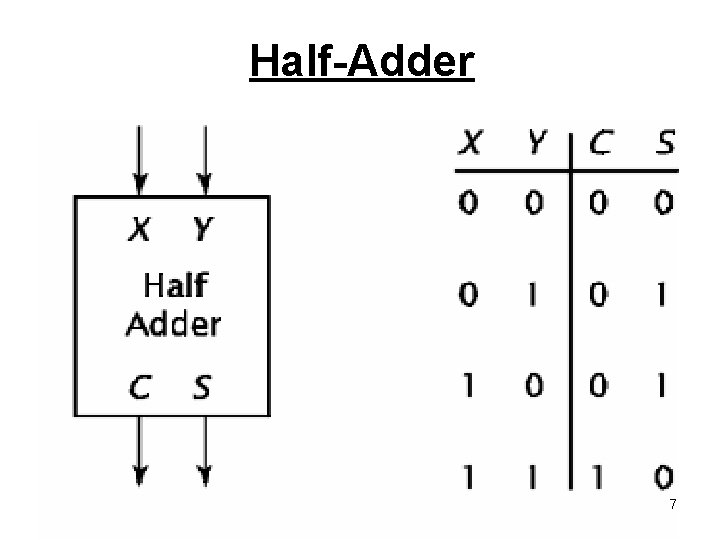
Half-Adder • A Half Adder (HA) is a 2 -input, 2 -output combinational circuit that adds the inputs and produces a Sum and a Carry • The Boolean expressions and the circuit for the Sum S and the carry C are given below: • Half adder – Inputs two 1 -bit values, X and Y – Outputs their 2 -bit sum as bits C and S • C is carry • S is the sum 5

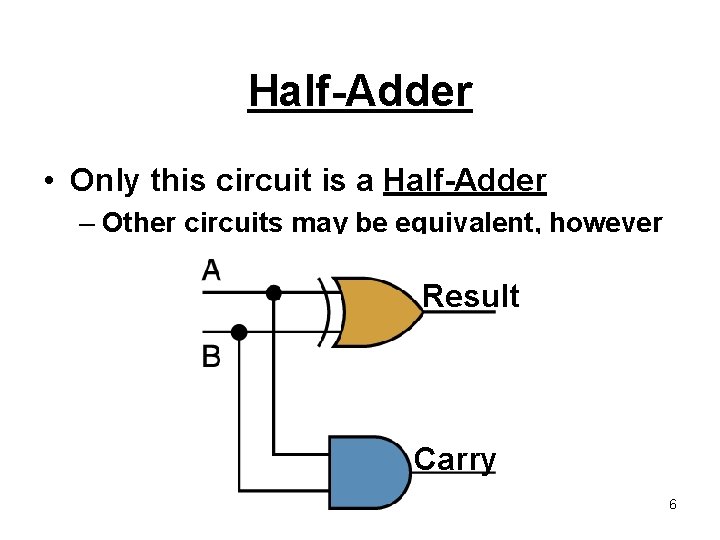
Half-Adder • Only this circuit is a Half-Adder – Other circuits may be equivalent, however Result Carry 6

Half-Adder 7

Half-Adder How to know a circuit is equivalent to half-adder ? • Circuit is equivalent to a half-adder if both truth tables have identical output • Cannot be used if there could be a carry-in bit So used to add least significant (rightmost) bit. Very important circuit in computers. • Addition is very common • Half-adder is found in every computer, calculator, digital watch… 8

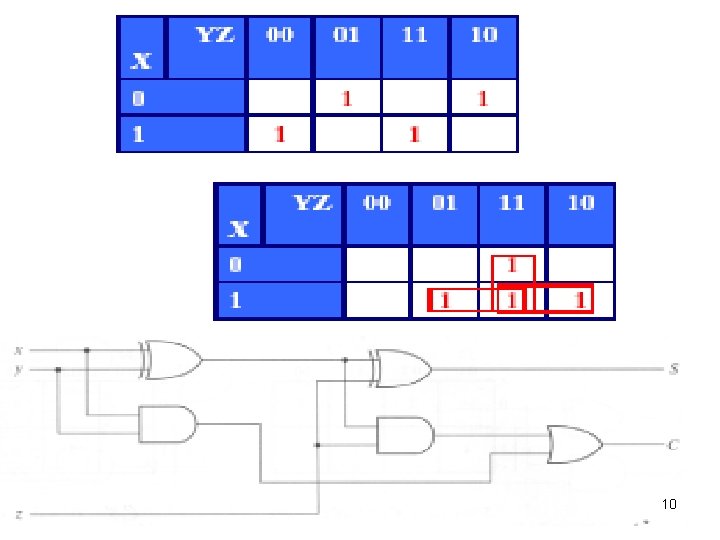
Binary Full Adder • A Full Adder (FA) is a 3 -input, 2 -output combinational circuit that adds the inputs and produces a Sum and a Carry • The third input can be perceived as the carry from a previous addition • The Boolean expressions and for the Sum S and the carry C, obtained from their K-Maps, are given below: 9

10

11

12

Multiplexer A multiplexer (MUX) is a device that accepts data from one of many input sources for transmission over a common shared line. To achieve this the MUX has several data lines and a single output along with data-select inputs, which permit digital data on any one of the inputs to be switched to the output line. The logic symbol for a 1 -of-4 data selector/ multiplexer is shown below, along with its associated table. Logic symbol for 1 -of-4 multiplexer 13

Active high MUX 14

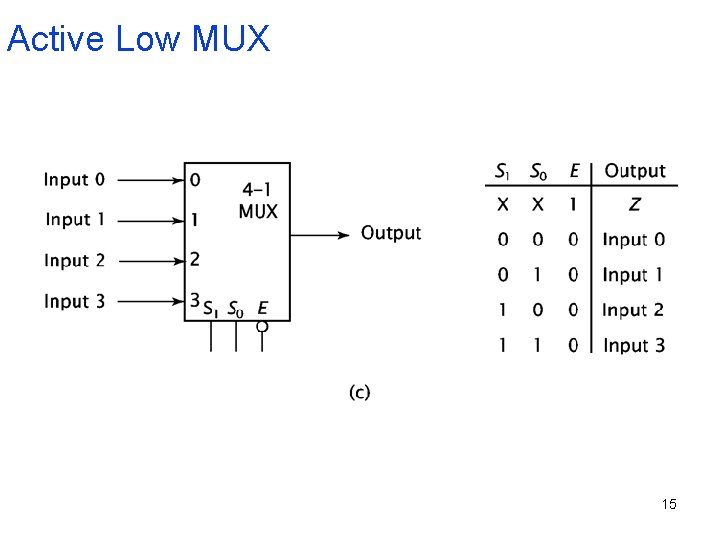
Active Low MUX 15

Data Select Inputs Input Selected S 1 S 0 0 0 D 0 0 1 D 1 1 0 D 2 1 1 D 3 Table of Operation Note that if a binary zero appears on the data-select lines then data on input line D 0 will appear on the output. Thus, data output Y is equal to D 0 if and only if S 1=0 and S 0=0 16

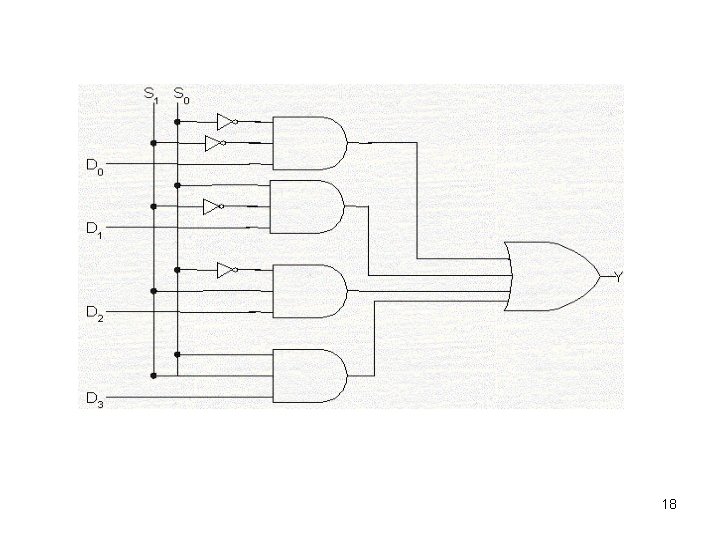
Similarly, the data output is equal to D 1, D 2 and D 3 for , and , respectively. Thus the total multiplexer logic expression, formed from ORing terms is 17

18

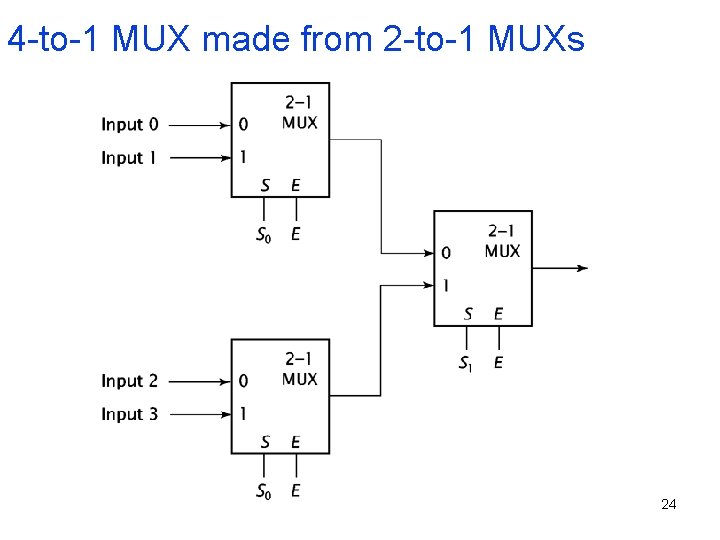
Larger MUX • Technique: use hierarchies of smaller components • Example: creating 4 x 1 mux from 2 x 1 mux – Will create a 2 -level mux tree – First level takes the initial inputs – The results from the first level are fed into the second level 19

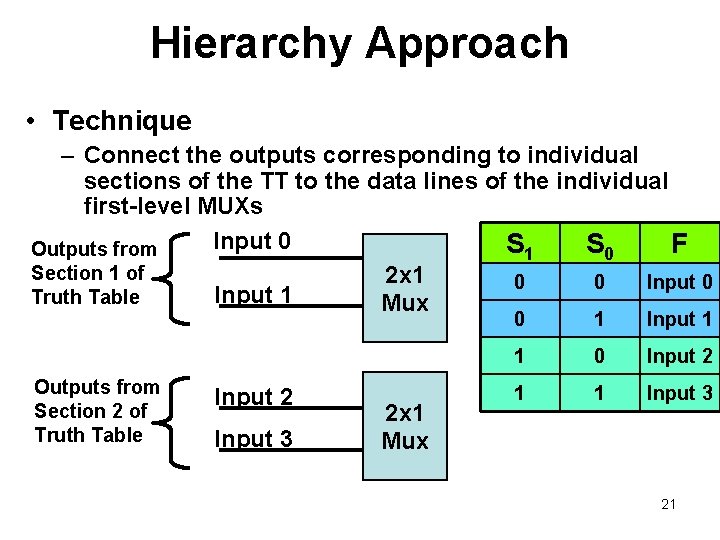
Hierarchy Approach • Technique – Divide the truth table into equal sections • Number of sections given by type of secondlevel MUX • If the second-level MUX is 2 x 1 then need 2 sections in the TT S 1 S 0 F 0 0 Input 0 0 1 Input 1 1 0 Input 2 1 1 Input 3 �� Section 1 �� Section 2 20

Hierarchy Approach • Technique – Connect the outputs corresponding to individual sections of the TT to the data lines of the individual first-level MUXs Input 0 S 1 S 0 F Outputs from Section 1 of 2 x 1 0 0 Input 1 Truth Table Mux Outputs from Section 2 of Truth Table Input 2 Input 3 2 x 1 Mux 0 1 Input 1 1 0 Input 2 1 1 Input 3 21

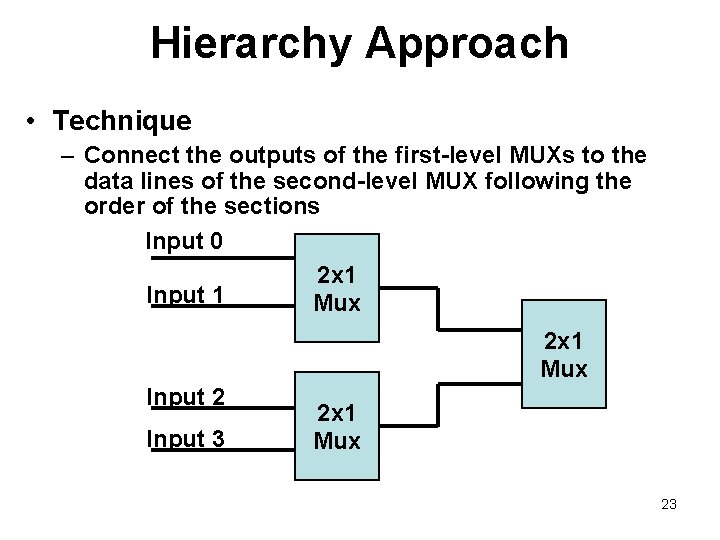
Hierarchy Approach • Technique – Connect the outputs of the first-level MUXs to the data lines of the second-level MUX following the order of the sections Input 0 2 x 1 Input 1 Mux 2 x 1 Mux Input 2 Input 3 2 x 1 Mux 22

Hierarchy Approach • Technique – Connect the outputs of the first-level MUXs to the data lines of the second-level MUX following the order of the sections Input 0 2 x 1 Input 1 Mux 2 x 1 Mux Input 2 Input 3 2 x 1 Mux 23

4 -to-1 MUX made from 2 -to-1 MUXs 24

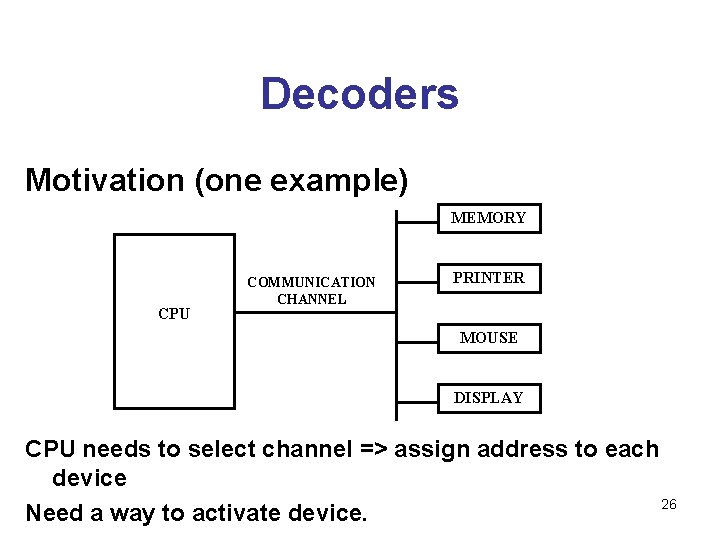
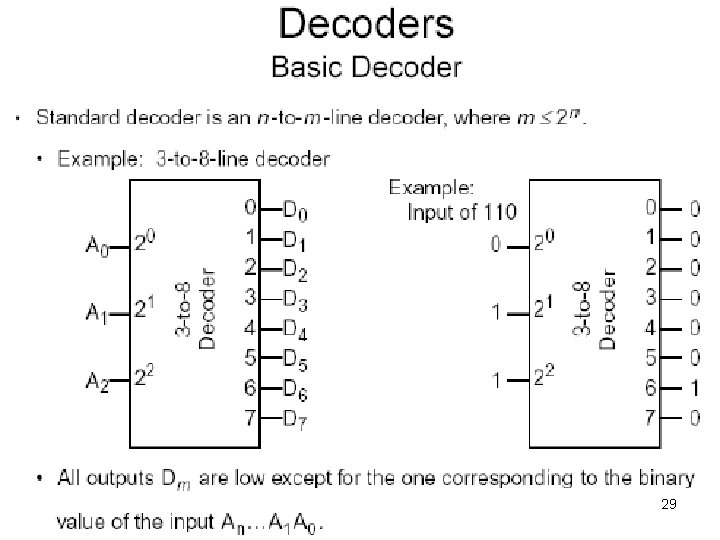
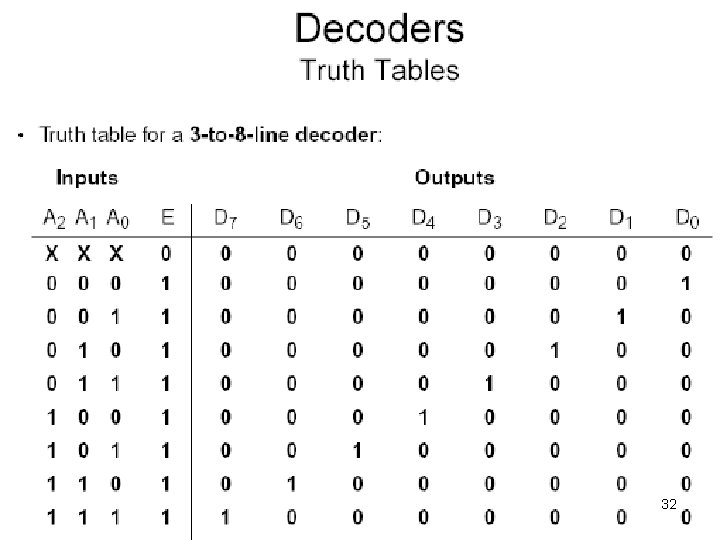
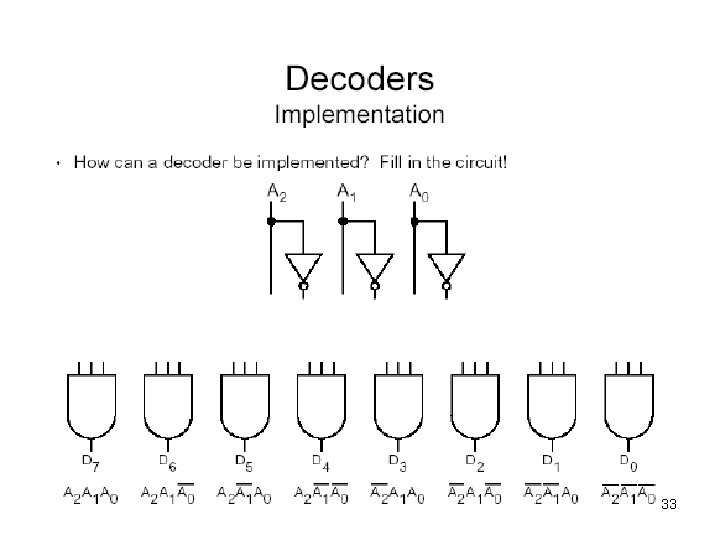
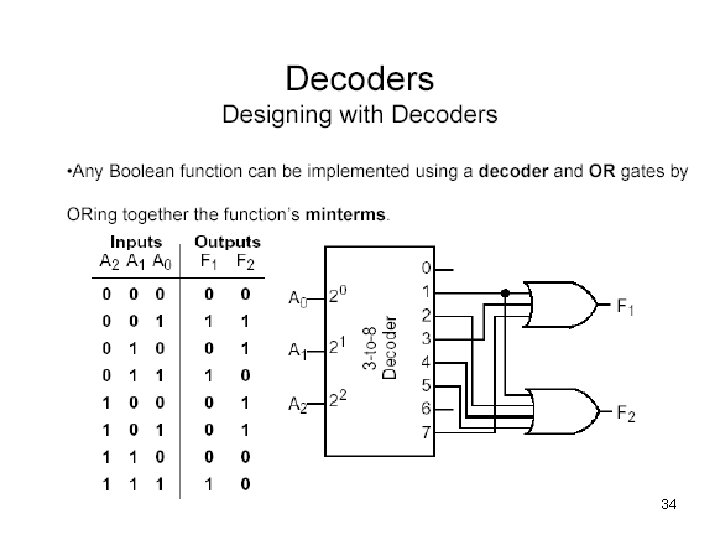
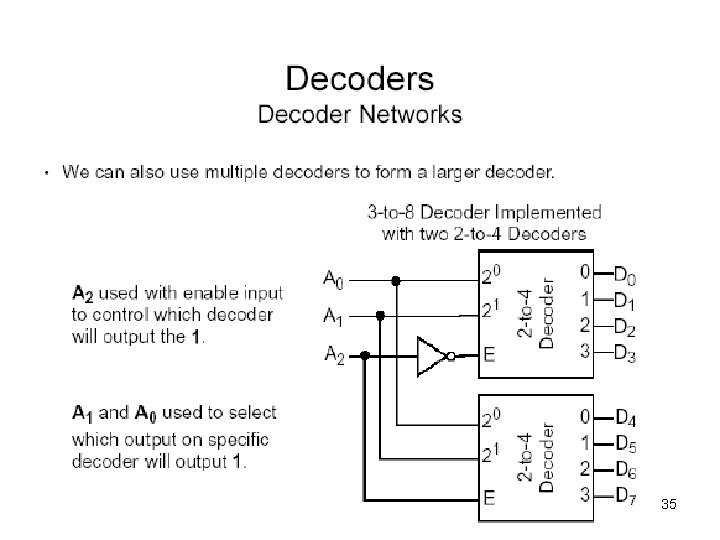
Decoders • A decoder: – Accepts a Boolean value (number) and activates the corresponding output line • All other lines are deactivated – For n inputs there are 2 n output lines • Each possible input value corresponds to an output line 25

Decoders Motivation (one example) MEMORY CPU COMMUNICATION CHANNEL PRINTER MOUSE DISPLAY CPU needs to select channel => assign address to each device 26 Need a way to activate device.

Decoders ACTIVATION LINE Motivation MEMORY ADDRESS CODE CPU PRINTER ADDRESS DECODER MOUSE DISPLAY CPU needs to select channel => assign address to each device Need a way to activate device. 27

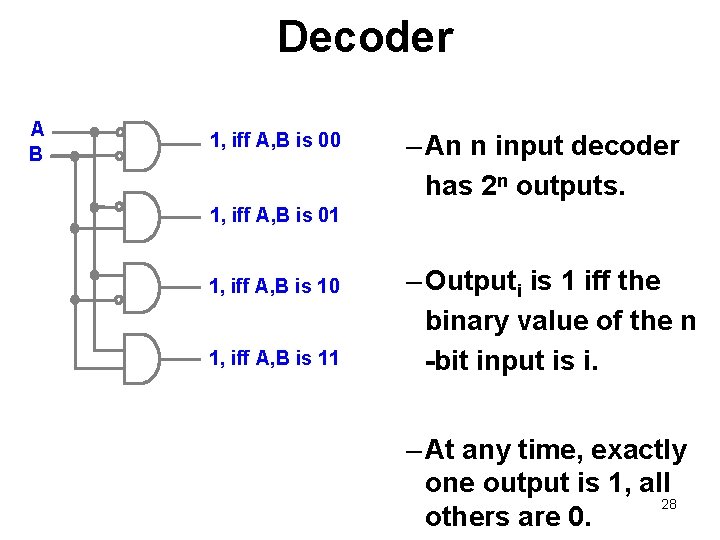
Decoder A B i = 0 1, iff A, B is 00 i = 1 1, iff A, B is 01 i = 2 1, iff A, B is 10 i = 3 1, iff A, B is 11 – An n input decoder has 2 n outputs. – Outputi is 1 iff the binary value of the n -bit input is i. – At any time, exactly one output is 1, all 28 others are 0.

29

30

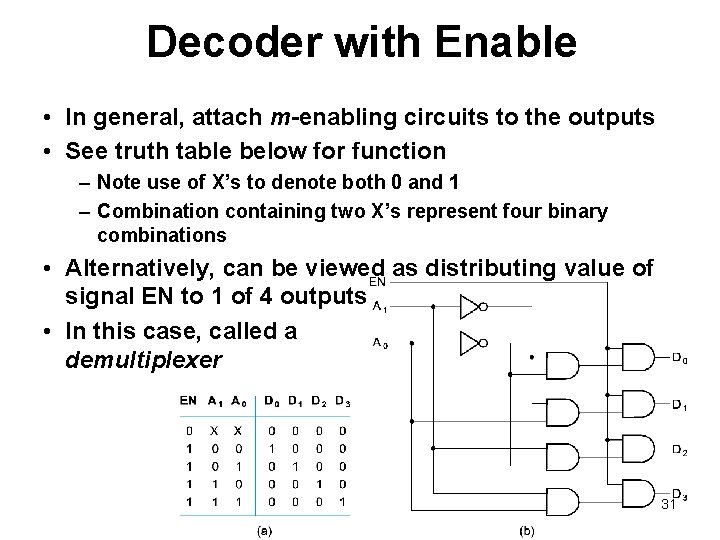
Decoder with Enable • In general, attach m-enabling circuits to the outputs • See truth table below for function – Note use of X’s to denote both 0 and 1 – Combination containing two X’s represent four binary combinations • Alternatively, can be viewed as distributing value of signal EN to 1 of 4 outputs • In this case, called a demultiplexer 31

32

33

34

35

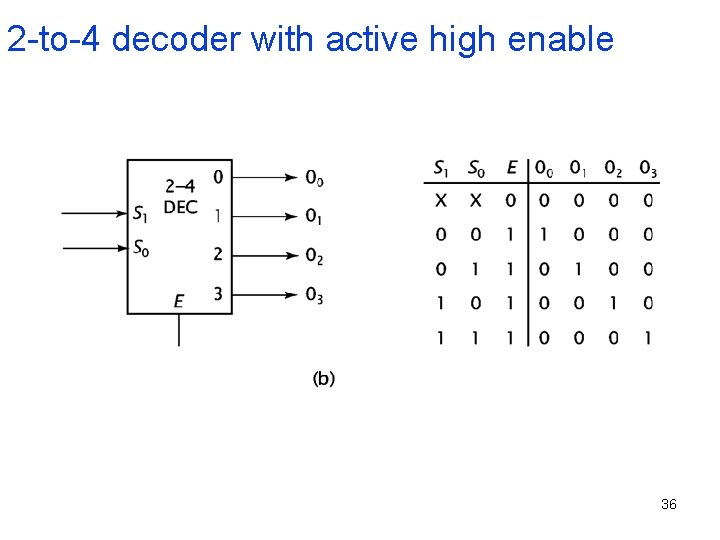
2 -to-4 decoder with active high enable 36

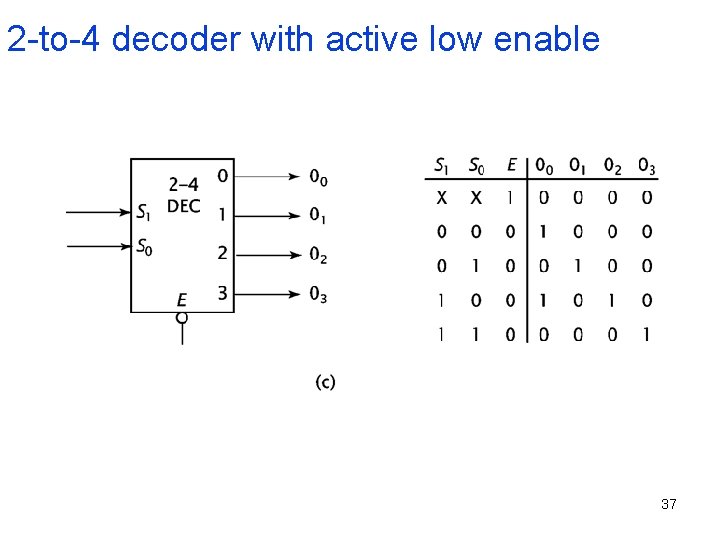
2 -to-4 decoder with active low enable 37

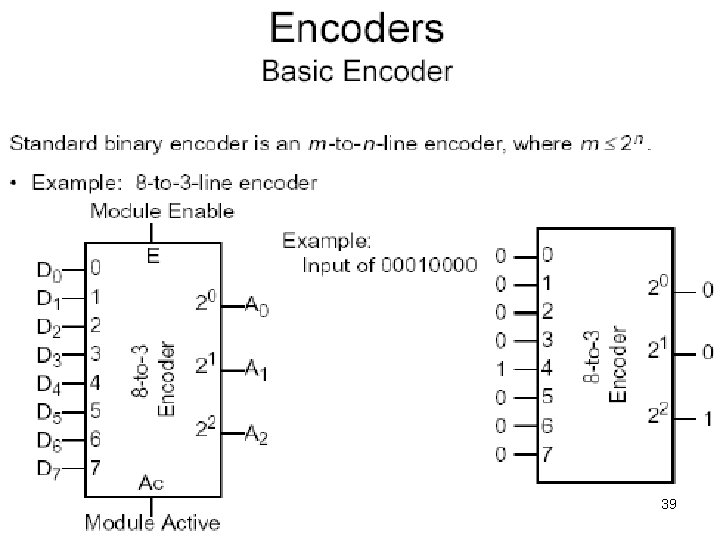
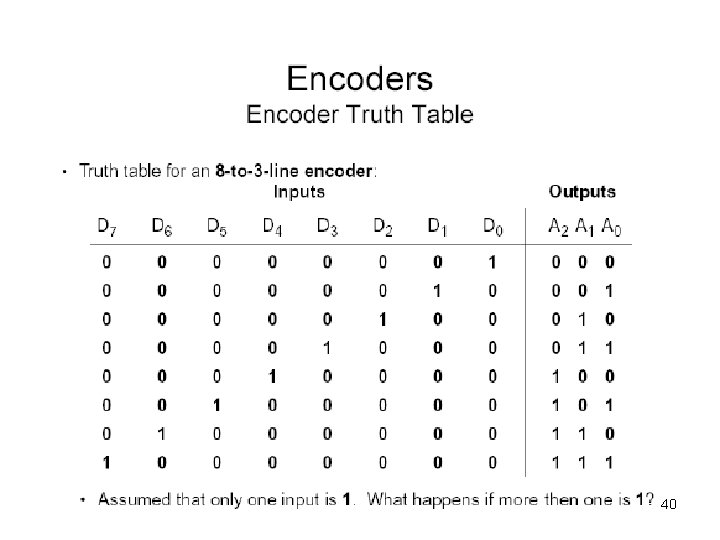
Encoders • An encoder: – For 2 n inputs there are n output lines • Outputs the Boolean value corresponding to the input line number • There is a special output line V that indicates whether any input lines are active. 38

39

40

41

42

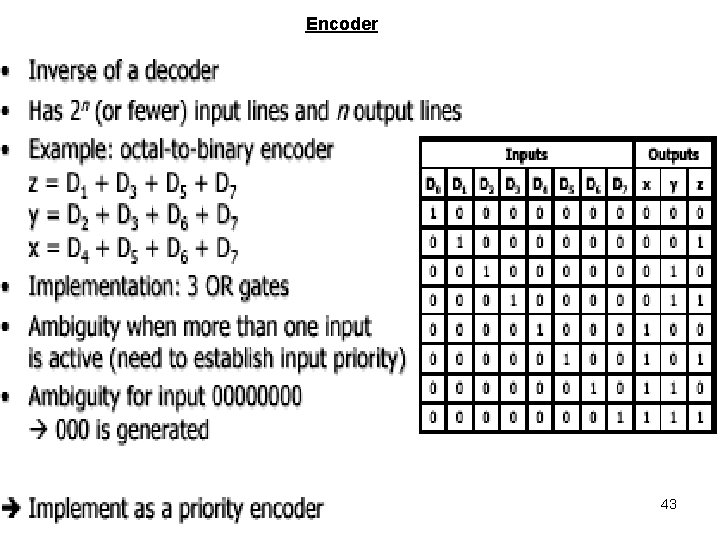
Encoder 43

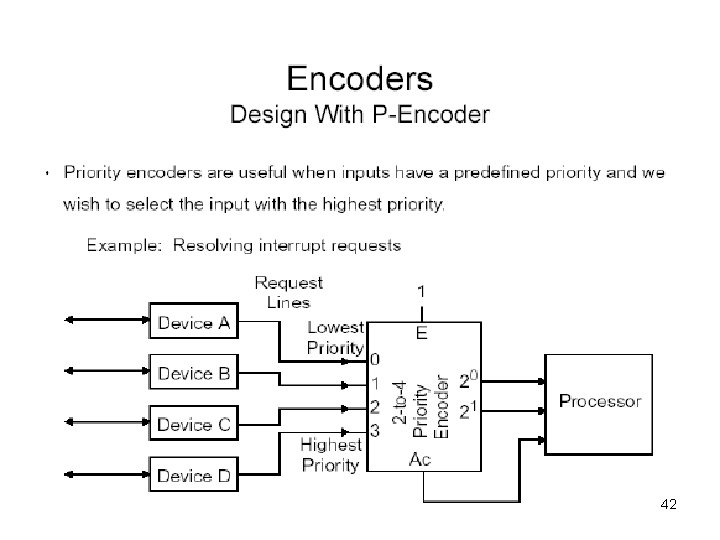
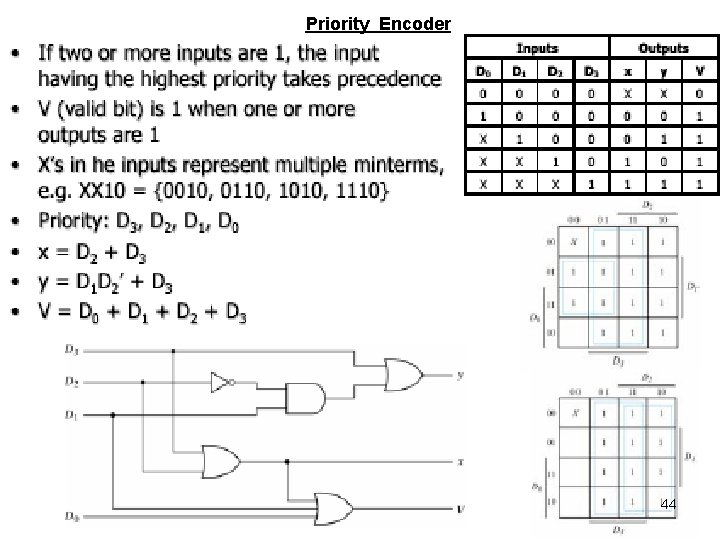
Priority Encoder 44