1 2 3 4 History of Particle Accelerators

History of Particle Accelerators — Livingston Plot 10 14 10 13 10 12 LHC

PAUL SCHERRER I N S T I T UT Energy gain Scalloping of the

How to Accelerate Charged Particles Assume: • an ultrarelativistic particle of charge e k

How to Accelerate Charged Particles not Then: • Position of the electron k ϑ

Lawson-Woodward-Palmer Theorem • Every wave in far field can be written as a superposition

Limits to the Accelerating Field • Normal-conducting accelerators • Breakdown on the surface •

Possibilities for Accelerating Structures Structure max. Field (V/m) Superconducting 5· 107 Power Sources solid

Laser as a source of electromagnetic 1. 2. 3. 4. fields Smaller/less expensive than

Laser Acceleration (1961) Koichi Shimoda, Applied Optics 1 (1), 33 (1961) Rasmus Ischebeck >

Semiconductor Industry Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09

Dielectric Accelerator Structures > Using much higher frequencies: THz to optical > Using dielectrics

Acceleration Experiments with a Dielectric Structure Laser pulse (λ = 800 nm) Magnetic lenses

Acceleration Experiments with a Dielectric Structure > Depending on their phase, some electrons are

Planar Structures: Measurements > Joel England Rasmus Ischebeck > Accelerator R&D Towards Highest Energies.

Dielectric Accelerators — Current Research Topics > Achievements of recent years > Proof-of-principle experiments

Efficiency of particle acceleration > Incorporate the accelerator structure into the laser cavity El

Plasma Wakefield Accelerators Rasmus Ischebeck

Plasma Wakes - Theory > Unlike electromagnetic waves in vacuum, plasma wakes can have

Plasma Wakes - Theory > Above this limit: non-linear wakes, “Blow-out regime” > Fields

Plasma Wakes - Reality Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016

Energy Doubling a Dispersion (mm) − 4 − 12 − 10 − 8 Energy

Measurement of Electromagnetic Fields Malte Kaluza, private communication Rasmus Ischebeck > Accelerator R&D Towards

Measurement of Electromagnetic Fields > Measurement of Plasma Wake (b/w) and Injected Electrons (color)

Staging of Two Accelerators Steinke et al. , Nature 530, 190 (2016) Rasmus Ischebeck

Drive the wake by a Proton Laser power supplies Beam Items in dark blue:

Plasma Accelerators — Current Research Topics > Achievements of recent years > Proof-of-principle experiments

Energy Efficiency 0 0 -50 Drive Bunch Direction -5 Accelerated Trailing Bunch 20 -100

Applicability of Plasma Wakefield Accelerators to HEP The Horizon 2020 Eu. PRAXIA Project Horizon

An Unfair Comparison 10 14 10 13 10 12 LHC Tevatron (Fermilab) 10 11

Slides: 35

Download presentation

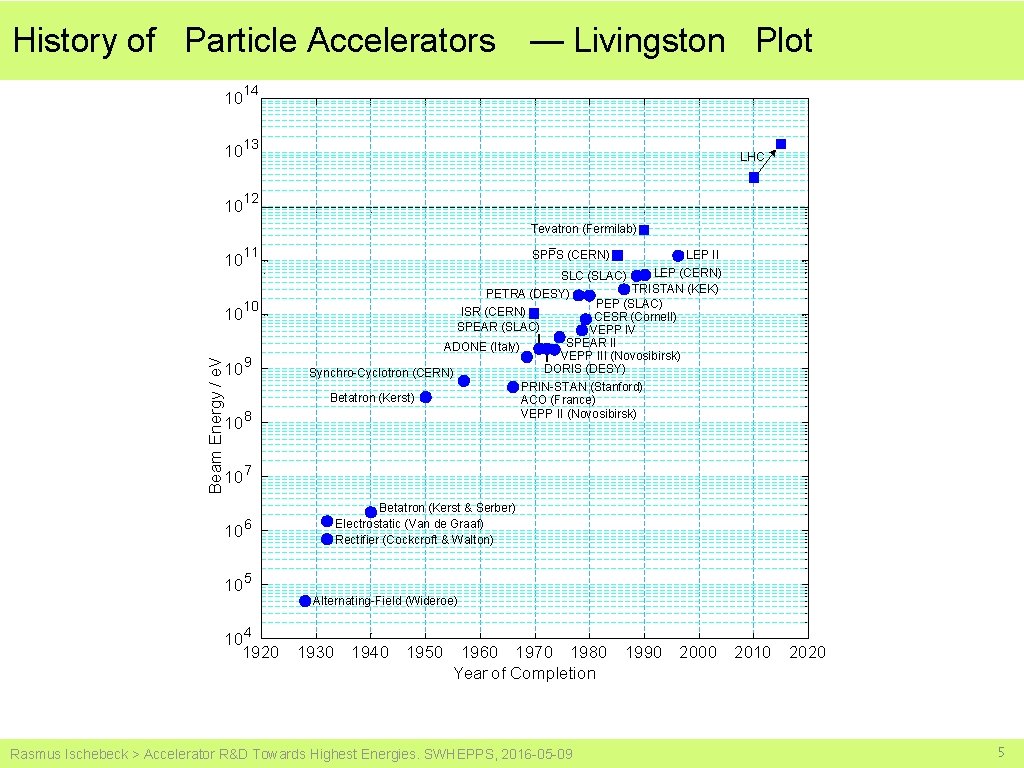
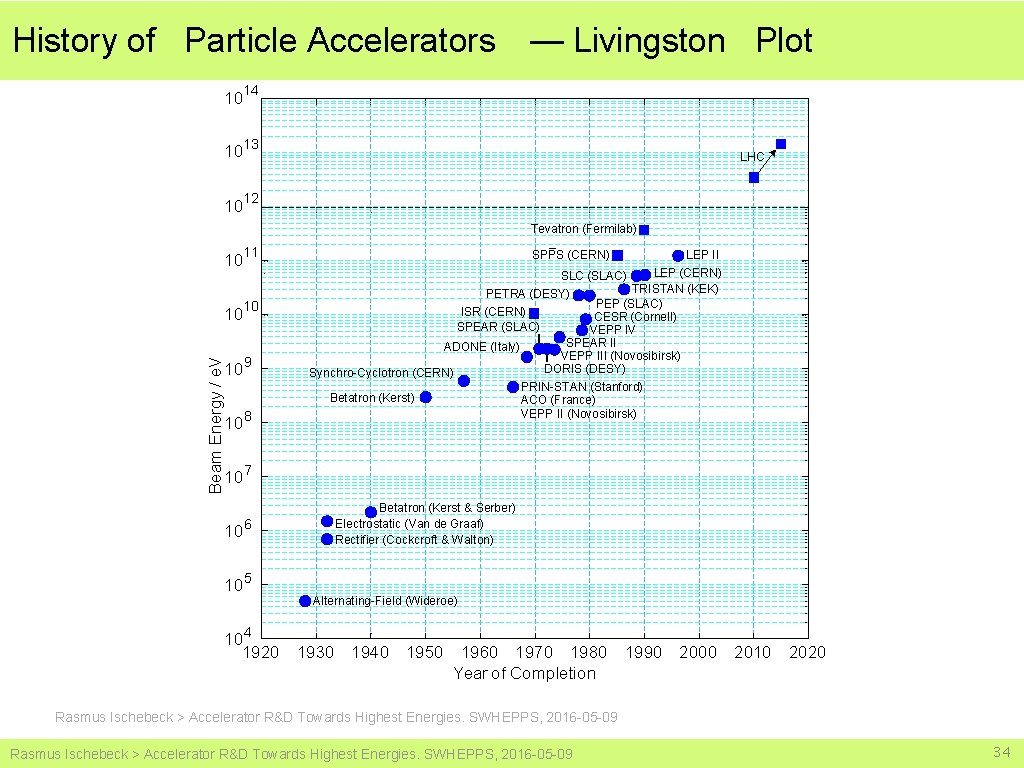
History of Particle Accelerators — Livingston Plot 10 14 10 13 10 12 LHC Tevatron (Fermilab) 10 11 10 10 9 10 8 10 7 Beam Energy / e. V 10 10 6 10 5 SPPS (CERN) LEP II LEP (CERN) SLC (SLAC) TRISTAN (KEK) PETRA (DESY) PEP (SLAC) ISR (CERN) CESR (Cornell) SPEAR (SLAC) VEPP IV SPEAR II ADONE (Italy) VEPP III (Novosibirsk) DORIS (DESY) Synchro-Cyclotron (CERN) PRIN-STAN (Stanford) Betatron (Kerst) ACO (France) VEPP II (Novosibirsk) Betatron (Kerst & Serber) Electrostatic (Van de Graaf) Rectifier (Cockcroft & Walton) Alternating-Field (Wideroe) 4 10 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 Year of Completion Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 5

PAUL SCHERRER I N S T I T UT Energy gain Scalloping of the beam Accelerator R&D Towards Highest Energies Rasmus Ischebeck, Paul Scherrer Institut

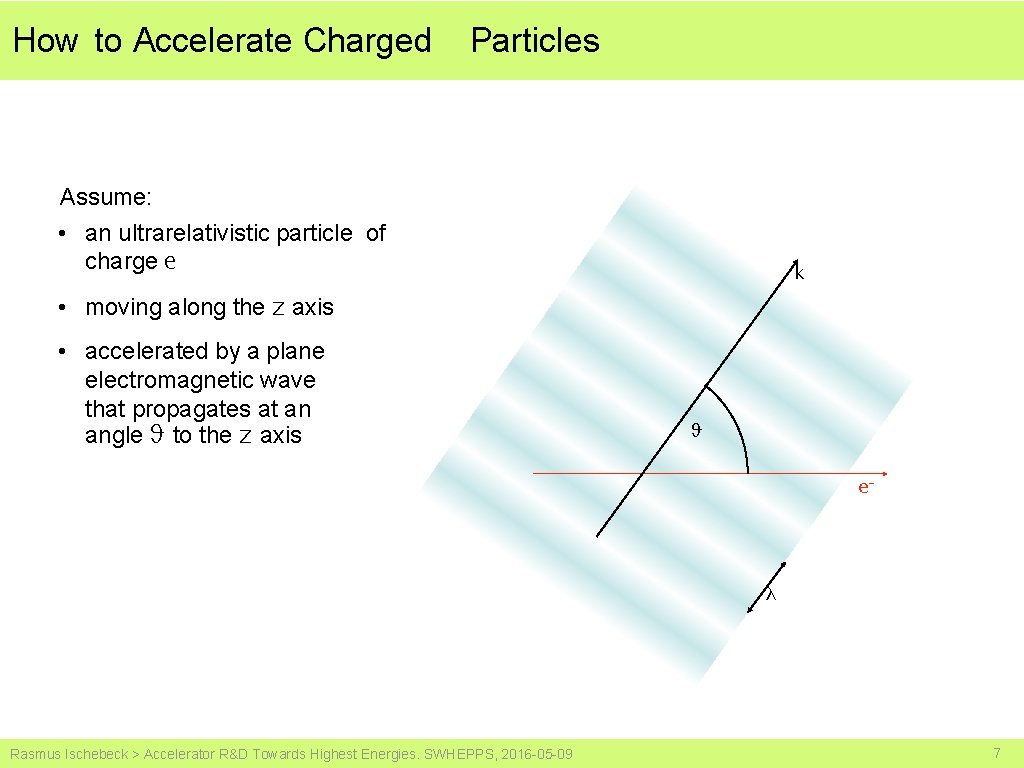
How to Accelerate Charged Particles Assume: • an ultrarelativistic particle of charge e k • moving along the z axis • accelerated by a plane electromagnetic wave that propagates at an angle ϑ to the z axis ϑ e- λ Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 7

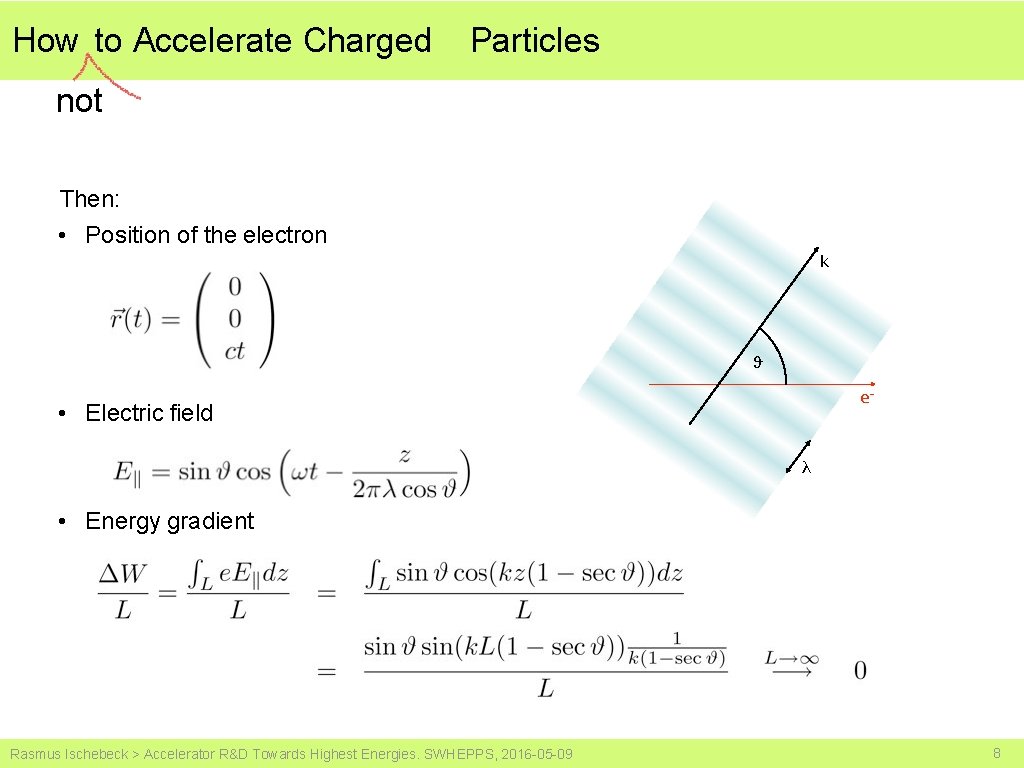
How to Accelerate Charged Particles not Then: • Position of the electron k ϑ e- • Electric field λ • Energy gradient Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 8

Lawson-Woodward-Palmer Theorem • Every wave in far field can be written as a superposition of plane waves • The Lawson-Woodward Theorem states: • the total acceleration • of ultrarelativistic particles • by far-field electromagnetic waves • is zero · Need near-field structures electron Woodward, J. IEE 93 (1947) Lawson, IEEE Trans. Nucl. Sci. 26 (1979) Palmer, Part. Accel. 11 (1980) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 electromagnetic wave 9

Limits to the Accelerating Field • Normal-conducting accelerators • Breakdown on the surface • Superconducting accelerators • Critical magnetic field http: //hyperphysics. phy-astr. gsu. edu/hbase/solids/scbc. html Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 10

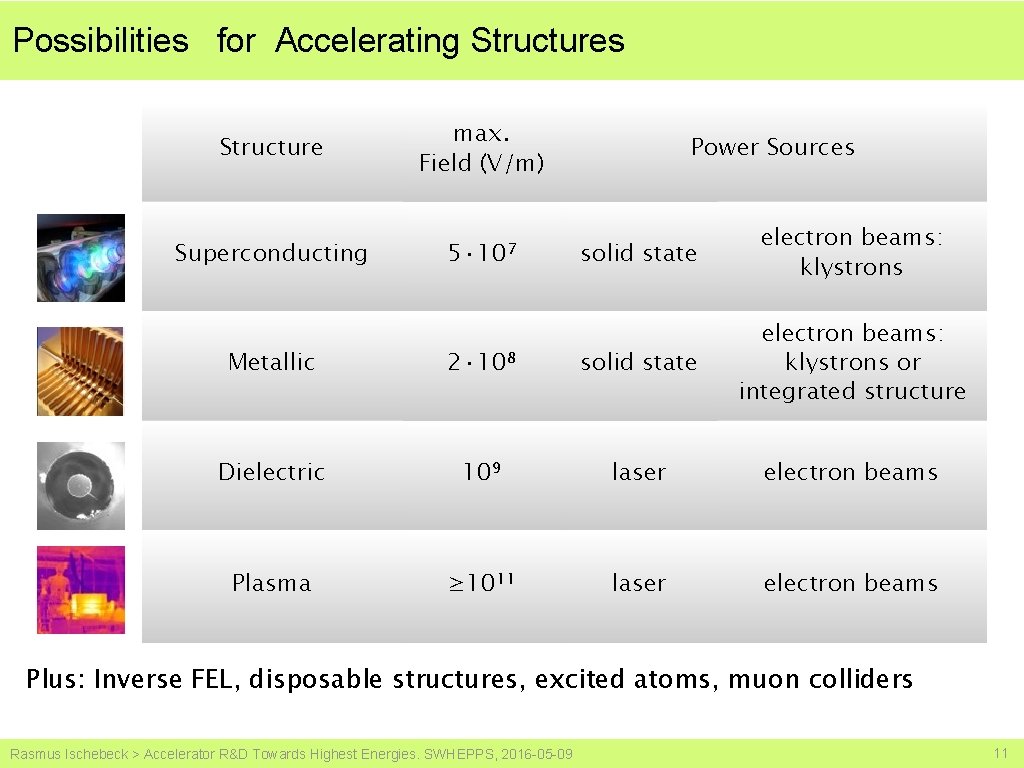
Possibilities for Accelerating Structures Structure max. Field (V/m) Superconducting 5· 107 Power Sources solid state electron beams: klystrons Metallic 2· 108 solid state electron beams: klystrons or integrated structure Dielectric 109 laser electron beams Plasma ≥ 1011 laser electron beams Plus: Inverse FEL, disposable structures, excited atoms, muon colliders Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 11

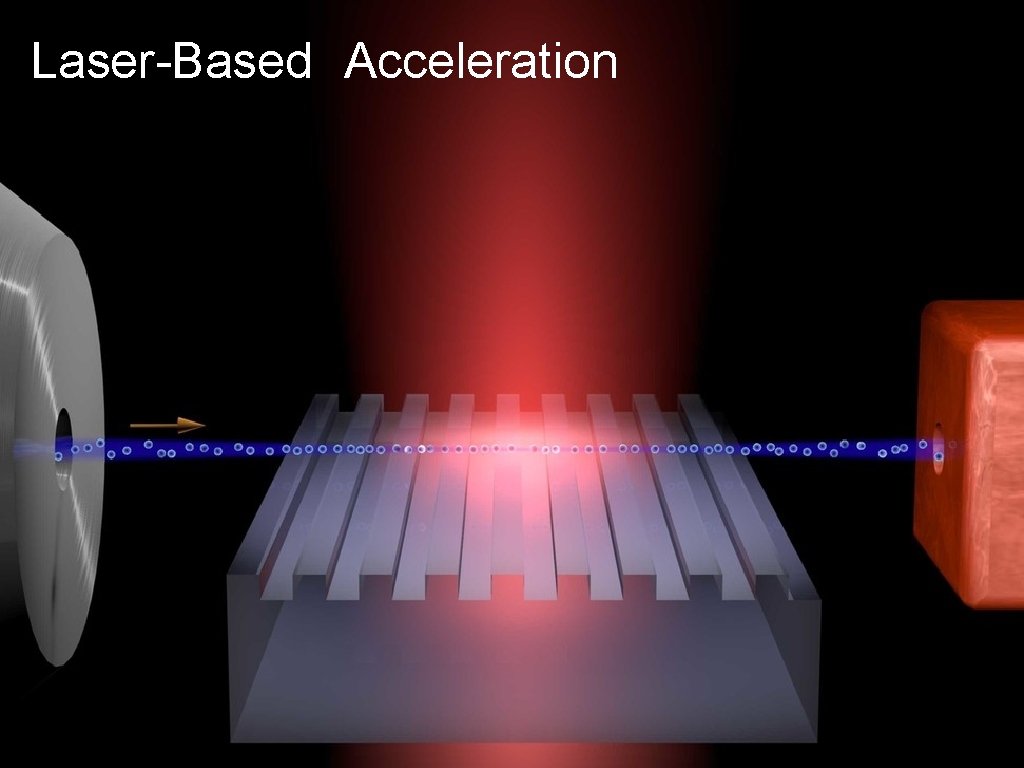
Laser-Based Acceleration

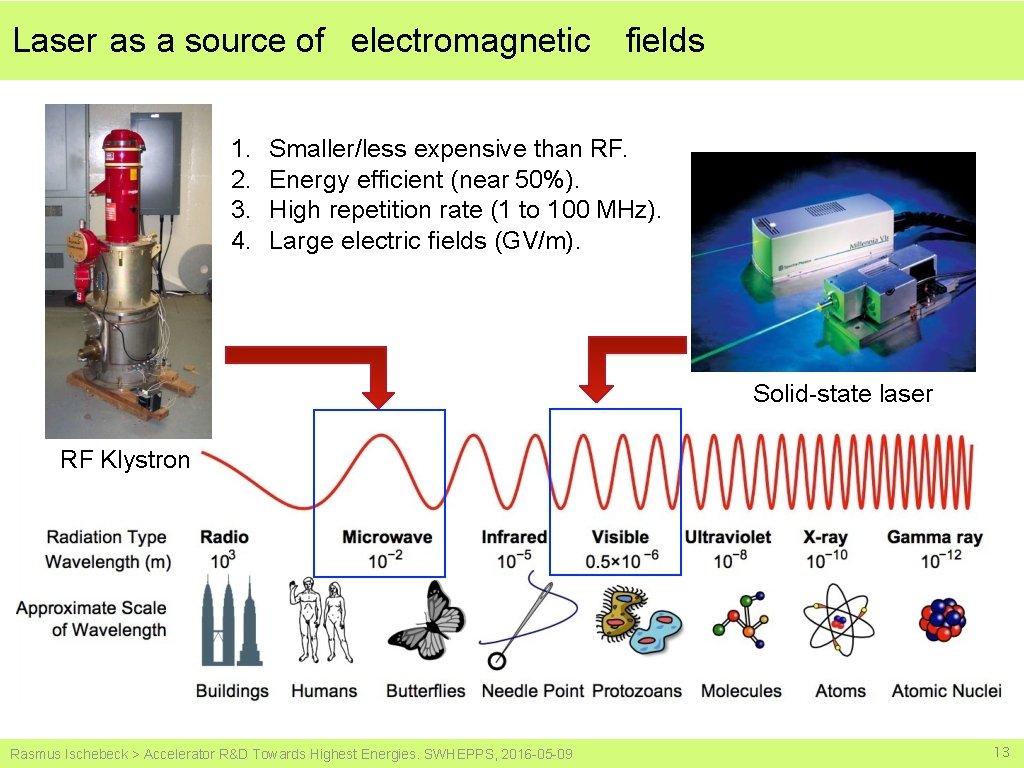
Laser as a source of electromagnetic 1. 2. 3. 4. fields Smaller/less expensive than RF. Energy efficient (near 50%). High repetition rate (1 to 100 MHz). Large electric fields (GV/m). Solid-state laser RF Klystron Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 13

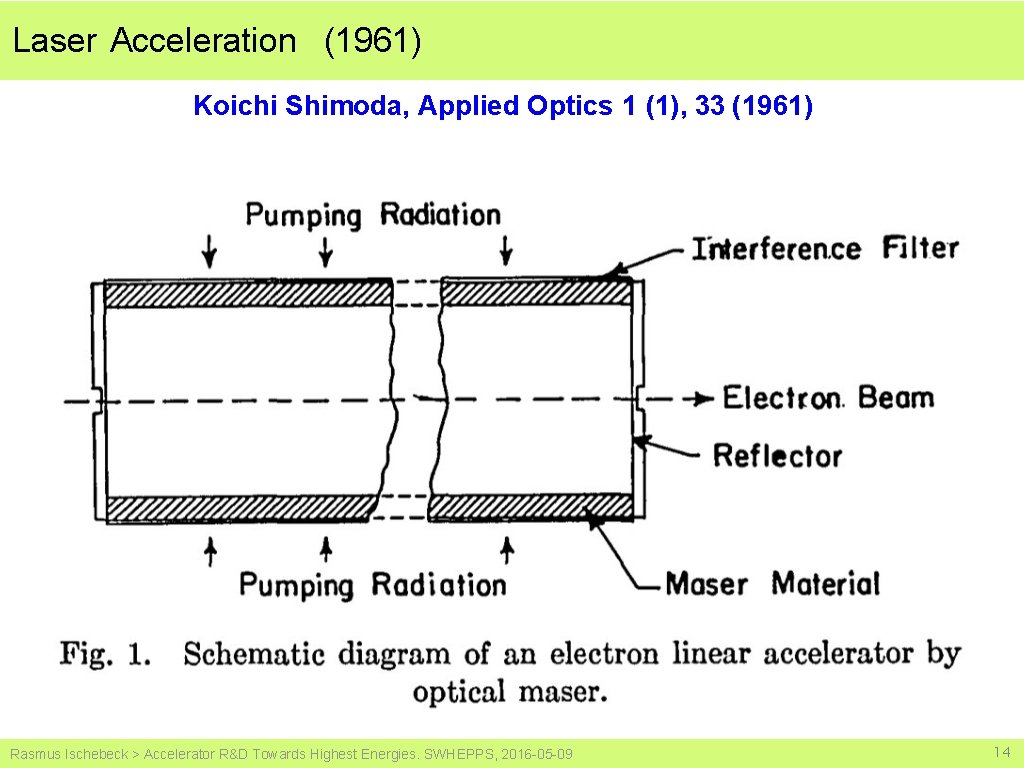
Laser Acceleration (1961) Koichi Shimoda, Applied Optics 1 (1), 33 (1961) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 14

Semiconductor Industry Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 15

Dielectric Accelerator Structures > Using much higher frequencies: THz to optical > Using dielectrics (e. g. Si. O 2) > Advantages: higher damage threshold · Higher accelerating fields, up to ~GV/m > Generate the electromagnetic field > Cherenkov radiation from an electron beam > Laser > Confine the field > Photonic band gap Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 8 16

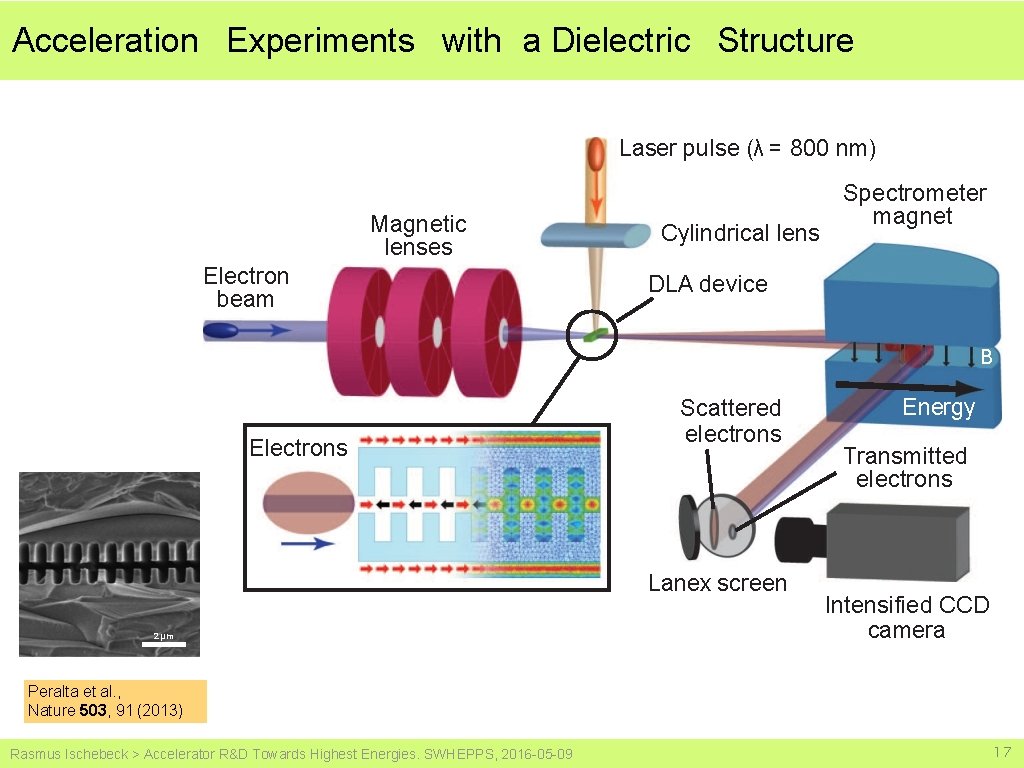
Acceleration Experiments with a Dielectric Structure Laser pulse (λ = 800 nm) Magnetic lenses Electron beam Cylindrical lens Spectrometer magnet DLA device B Electrons Scattered electrons Lanex screen 2 μm Energy Transmitted electrons Intensified CCD camera Peralta et al. , Nature 503, 91 (2013) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 17

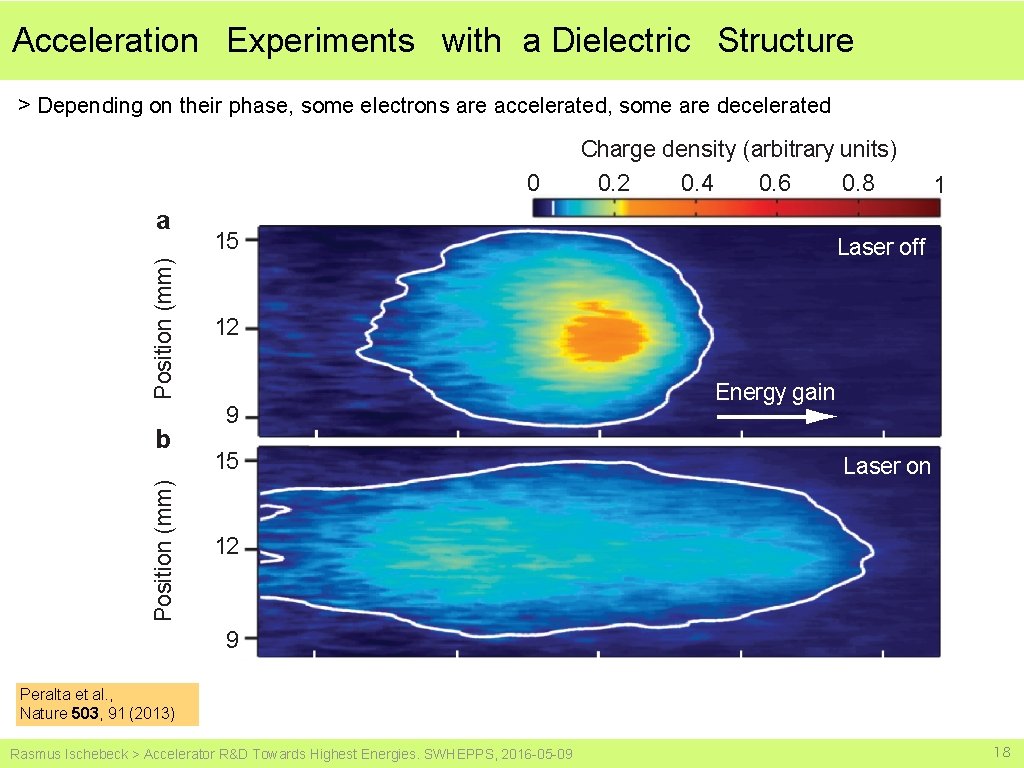
Acceleration Experiments with a Dielectric Structure > Depending on their phase, some electrons are accelerated, some are decelerated 0 Position (mm) a Position (mm) b Charge density (arbitrary units) 0. 2 0. 4 0. 6 0. 8 15 1 Laser off 12 9 15 Energy gain Laser on 12 9 Peralta et al. , Nature 503, 91 (2013) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 18

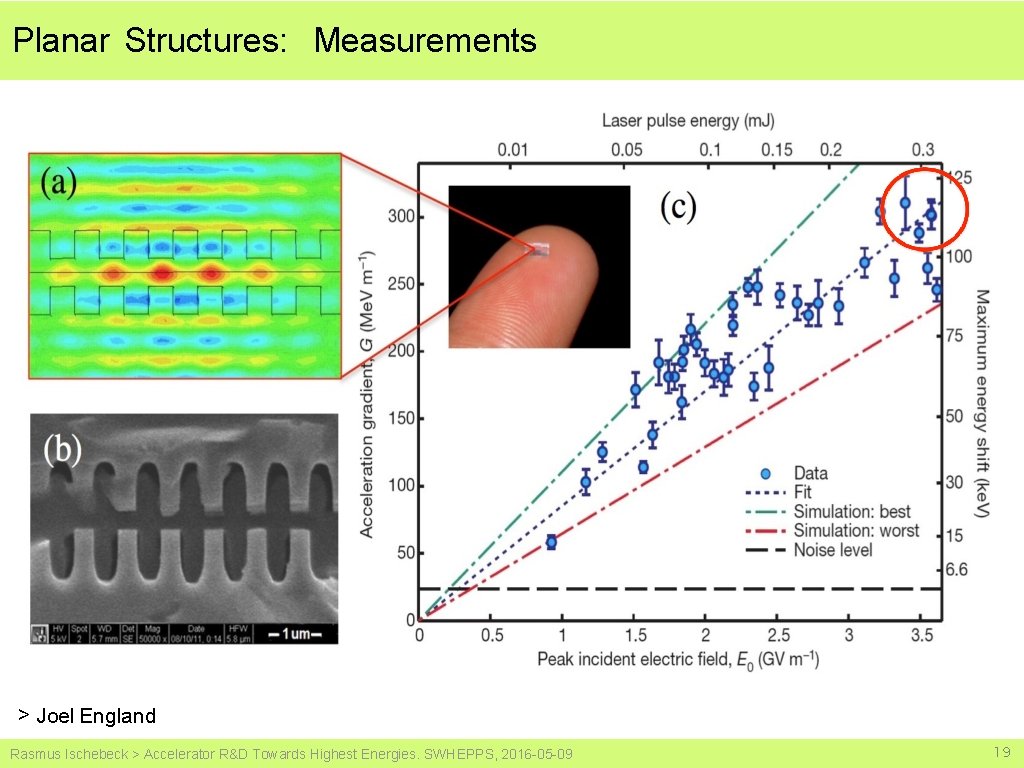
Planar Structures: Measurements > Joel England Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 19

Dielectric Accelerators — Current Research Topics > Achievements of recent years > Proof-of-principle experiments demonstrating accelerating fields of GV/m > Efficient generation of the electromagnetic fields > Ongoing research projects > Accelerating of high-charge bunches > Staging of accelerating structures > Damage threshold of the materials (laser, electrons) > Future research topics > Efficient coupling of the electromagnetic fields > Confinement by photonic band gap structures > Acceleration of ions > Efficiency of particle acceleration Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 20

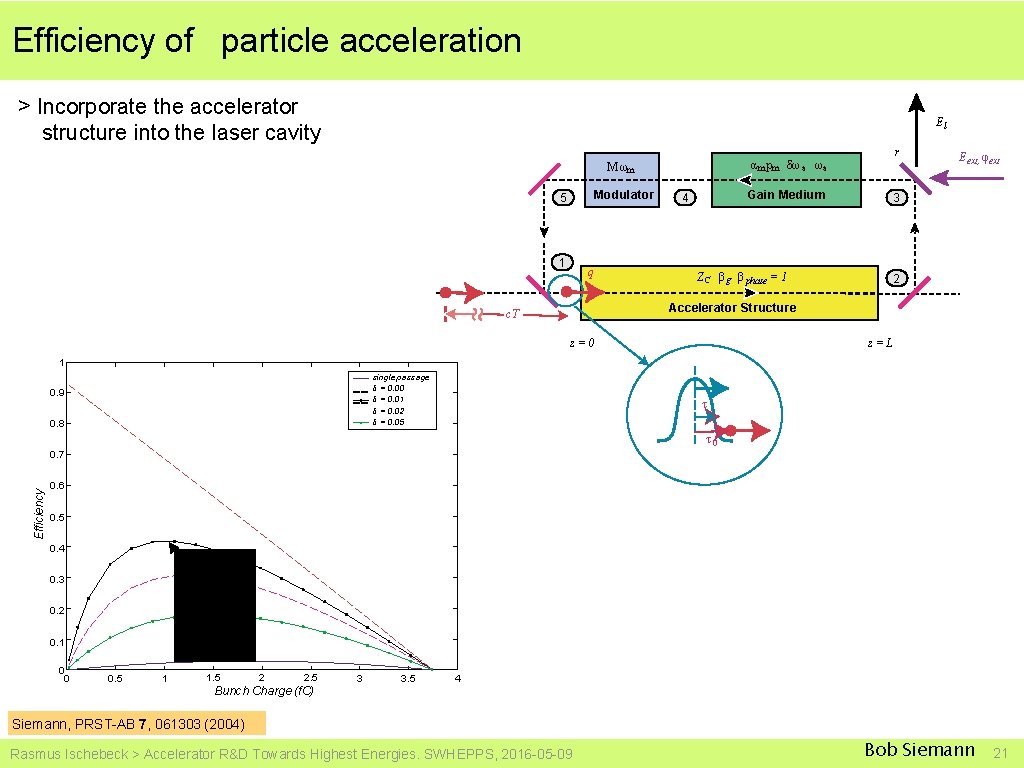
Efficiency of particle acceleration > Incorporate the accelerator structure into the laser cavity El α mpm δω a ωa Μ ωm Modulator 5 1 q r Gain Medium 4 Eext, φext 3 ZC β g β phase = 1 2 Accelerator Structure c. T z =0 z =L 1 single passage δ = 0. 00 δ = 0. 01 δ = 0. 02 δ = 0. 05 0. 9 0. 8 τ τ0 Efficiency 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 0 0. 5 1 1. 5 2 2. 5 Bunch Charge (f. C) 3 3. 5 4 Siemann, PRST-AB 7, 061303 (2004) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 Bob Siemann 21

Plasma Wakefield Accelerators Rasmus Ischebeck

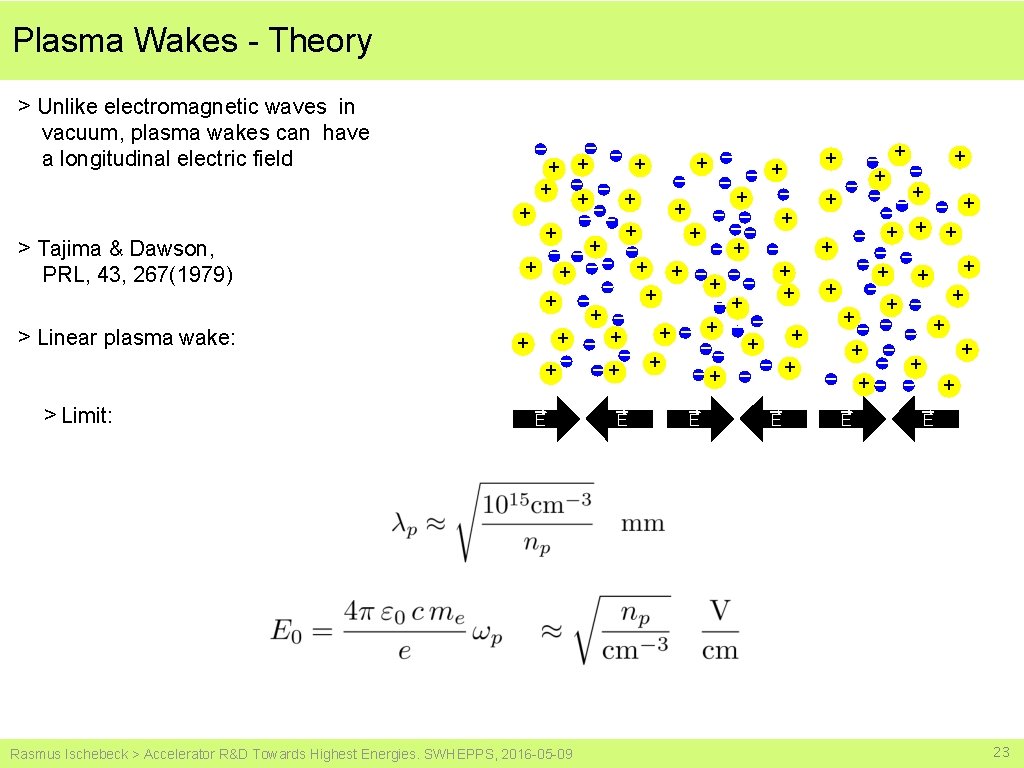
Plasma Wakes - Theory > Unlike electromagnetic waves in vacuum, plasma wakes can have a longitudinal electric field > Tajima & Dawson, PRL, 43, 267(1979) > Linear plasma wake: > Limit: – – + + + + – – – + + + – –– + – – + + –– + + – – + + + – –+ + – – – + + + –+ – – E Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 E E E + + – + – – + + – – – + + + – – + + – + – – – + + + – – + +– – + E E 23

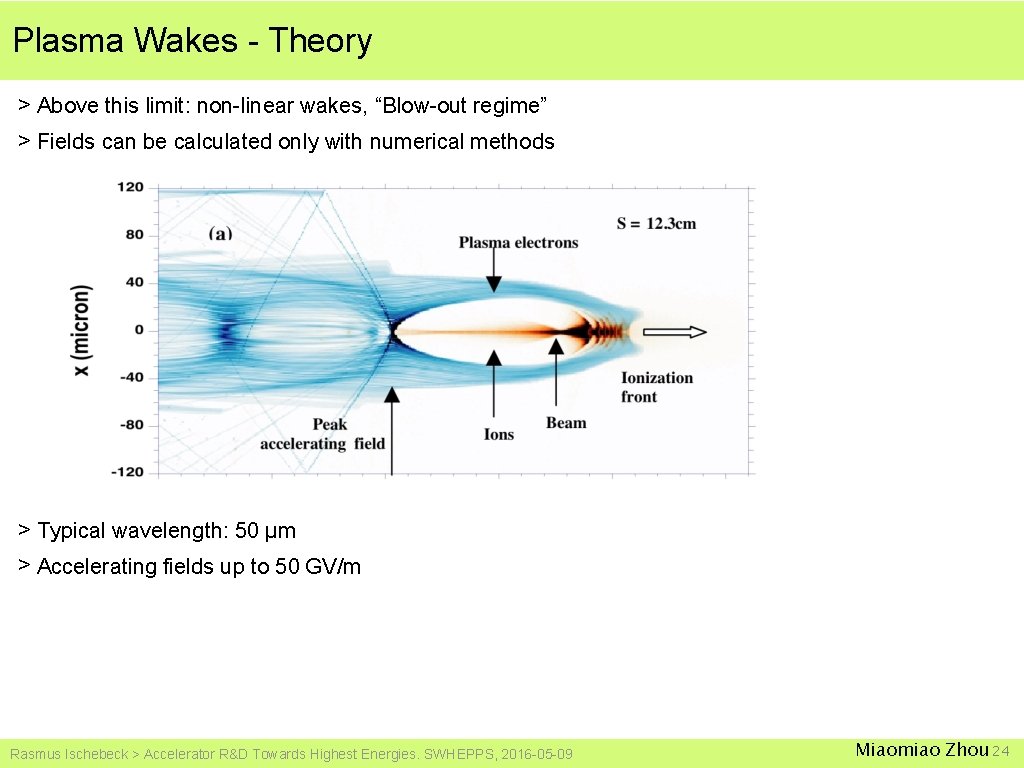
Plasma Wakes - Theory > Above this limit: non-linear wakes, “Blow-out regime” > Fields can be calculated only with numerical methods > Typical wavelength: 50 µm > Accelerating fields up to 50 GV/m Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 Miaomiao Zhou 24

Plasma Wakes - Reality Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 25

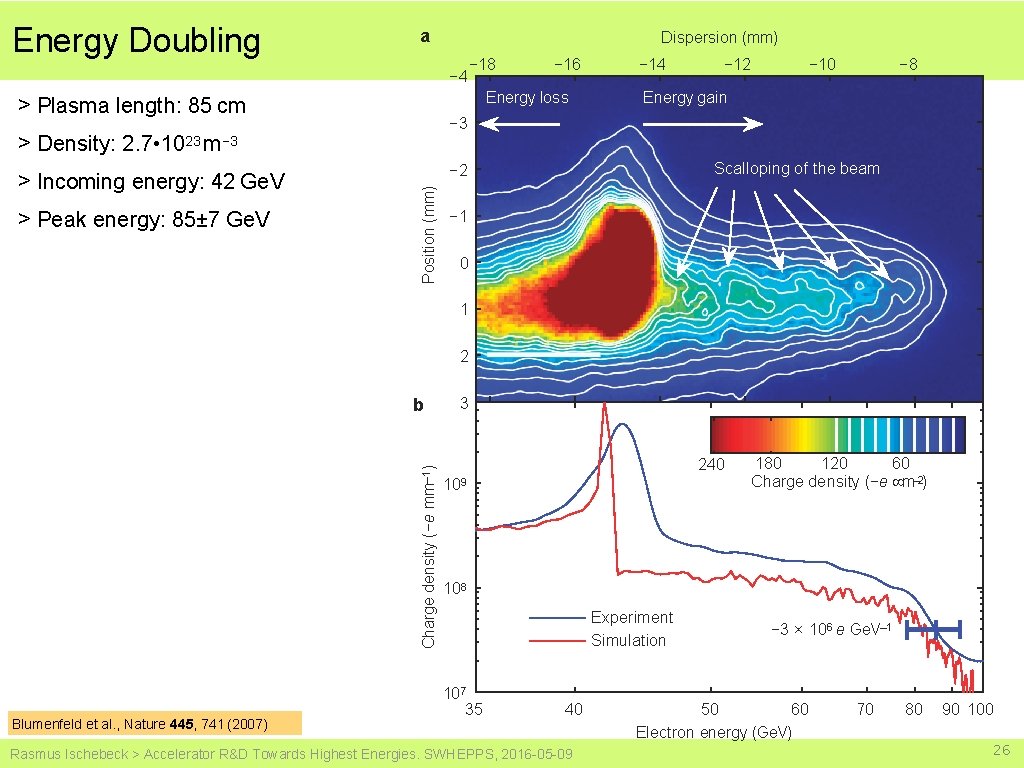
Energy Doubling a Dispersion (mm) − 4 − 12 − 10 − 8 Energy gain − 3 > Density: 2. 7 • 1023 m− 3 Scalloping of the beam − 2 Position (mm) > Peak energy: 85± 7 Ge. V − 16 Energy loss > Plasma length: 85 cm > Incoming energy: 42 Ge. V − 18 − 1 0 1 2 Charge density (−e mm– 1) b Blumenfeld et al. , Nature 445, 741 (2007) 3 240 109 180 120 60 Charge density (−e µm– 2) 108 Experiment Simulation 107 35 40 Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 − 3 × 106 e Ge. V– 1 50 60 Electron energy (Ge. V) 70 80 90 100 26

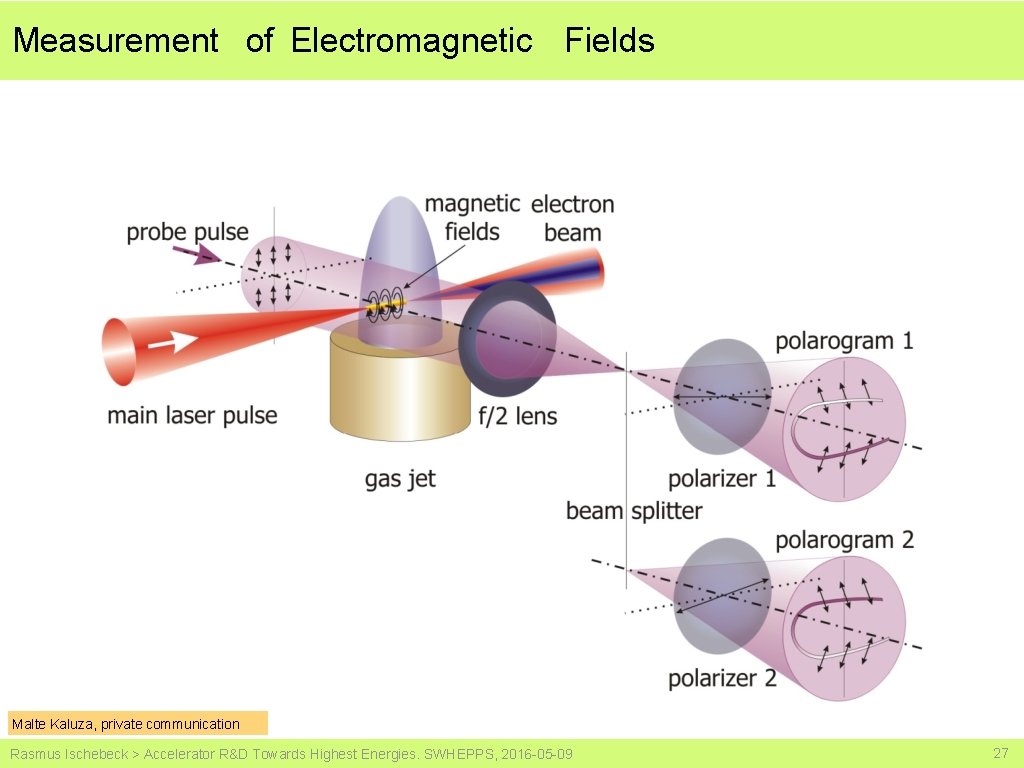
Measurement of Electromagnetic Fields Malte Kaluza, private communication Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 27

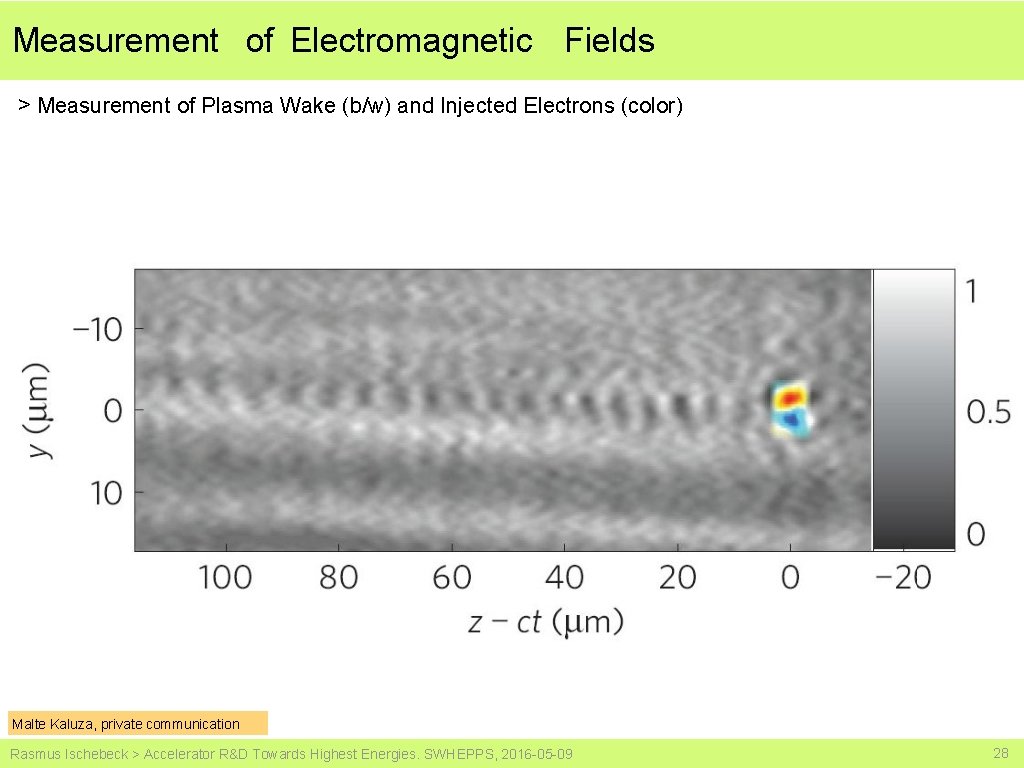
Measurement of Electromagnetic Fields > Measurement of Plasma Wake (b/w) and Injected Electrons (color) Malte Kaluza, private communication Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 28

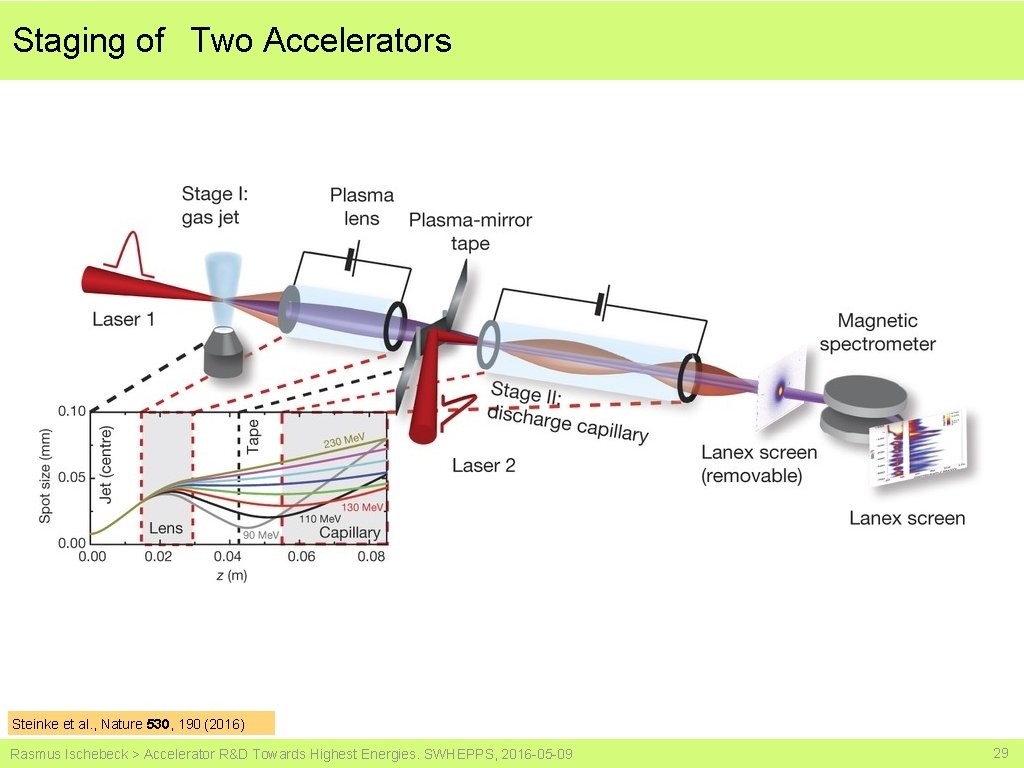
Staging of Two Accelerators Steinke et al. , Nature 530, 190 (2016) Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 29

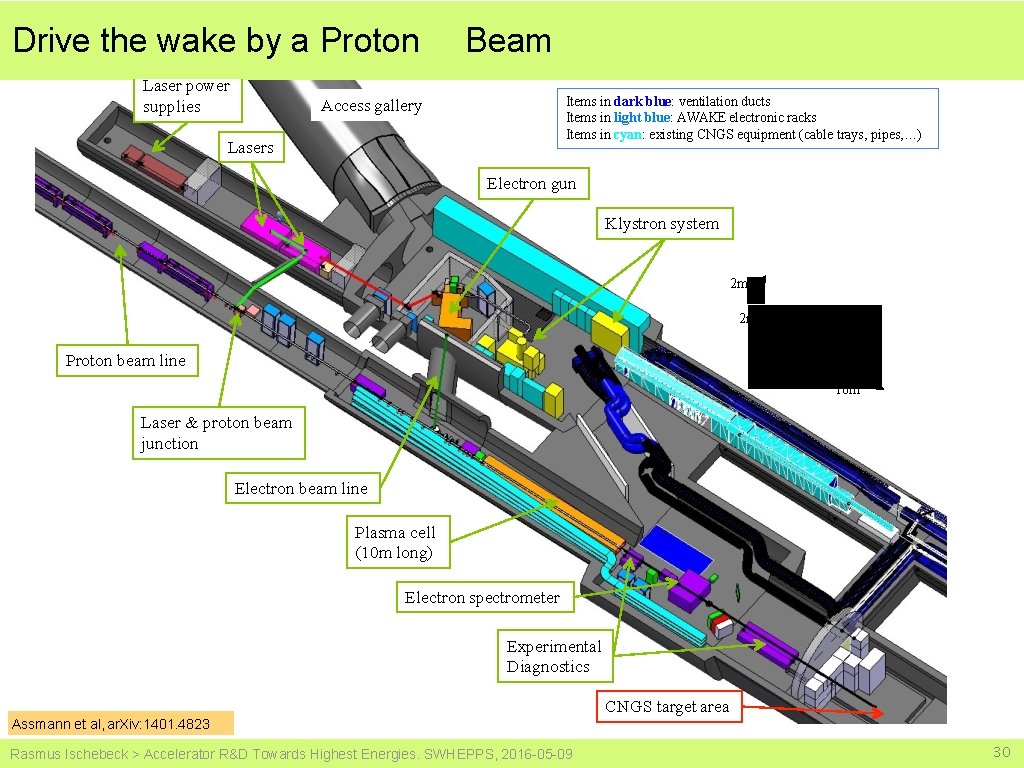
Drive the wake by a Proton Laser power supplies Beam Items in dark blue: ventilation ducts Items in light blue: AWAKE electronic racks Items in cyan: existing CNGS equipment (cable trays, pipes, …) Access gallery Lasers Electron gun Klystron system 2 m 2 m Proton beam line 10 m Laser & proton beam junction Electron beam line Plasma cell (10 m long) Electron spectrometer Experimental Diagnostics Assmann et al, ar. Xiv: 1401. 4823 Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 CNGS target area 30

Plasma Accelerators — Current Research Topics > Achievements of recent years > Proof-of-principle experiments demonstrating accelerating fields of tens of GV/m > Meter-scale plasmas that allow high energy gain > Characterization of plasma wakes > Ongoing research projects > Staging of accelerating structures > Control energy spread > Efficiency of particle acceleration > Future research topics > Efficient generation of plasma wakes with proton beams > Match electron beam into plasma with micrometer precision Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 31

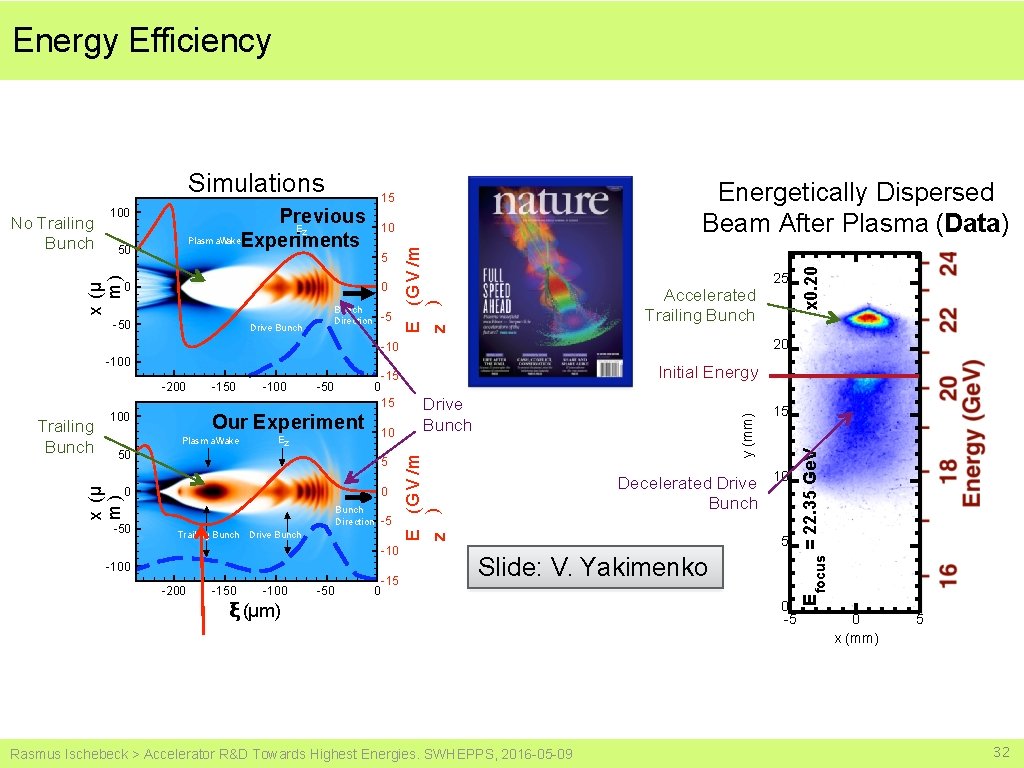
Energy Efficiency 0 0 -50 Drive Bunch Direction -5 Accelerated Trailing Bunch 20 -100 -50 0 ξ (μm) Plasm a Wake 10 Ez 5 0 -50 0 Bunch Direction Trailing B unch -5 Drive Bunch -100 -200 -150 -100 ξ (μm) -50 0 Initial Energy -15 15 Our Experiment 50 x (μ m) Bunch -100 -15 Drive Bunch y (mm) b 100 Trailing -150 E (G V /m z ) -200 25 x 0. 20 5 15 Decelerated Drive 10 Bunch 5 Slide: V. Yakimenko Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 = 22. 35 Ge. V x (μ m) 50 10 focus Previous Ez Plasm a. Wak e. Experiments E (G V /m z ) a 100 No Trailing Bunch Energetically Dispersed Beam After Plasma (Data) 15 0 -5 C E Simulations 0 x (mm) 5 32

Applicability of Plasma Wakefield Accelerators to HEP The Horizon 2020 Eu. PRAXIA Project Horizon 2020 Towards a Groundbreaking European Plasma Accelerator Eu. PRAXIA Consor. Vum Plus 16 Associated Partners > Arnd Specka, Ecole Polytechnique Paris > Roman Walczak, Uni Oxford > Meeting Paris October 2016 Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 33

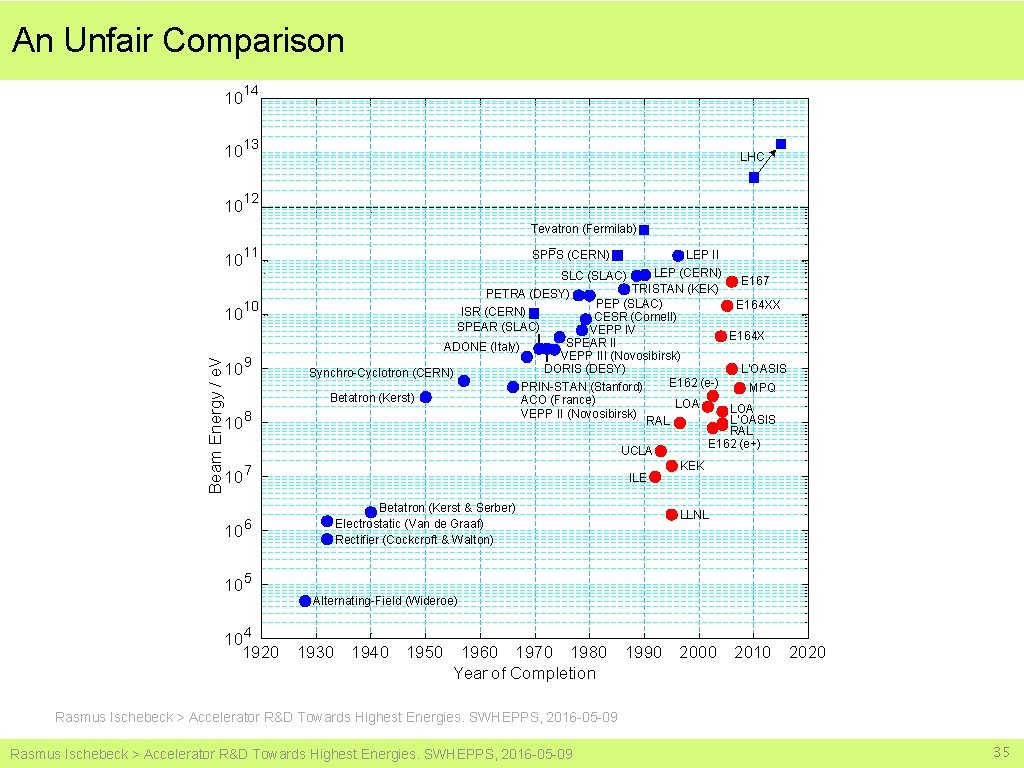
An Unfair Comparison 10 14 10 13 10 12 LHC Tevatron (Fermilab) 10 11 10 10 9 10 8 10 7 Beam Energy / e. V 10 10 6 10 5 SPPS (CERN) LEP II LEP (CERN) SLC (SLAC) E 167 TRISTAN (KEK) PETRA (DESY) PEP (SLAC) E 164 XX ISR (CERN) CESR (Cornell) SPEAR (SLAC) VEPP IV E 164 X SPEAR II ADONE (Italy) VEPP III (Novosibirsk) L’OASIS DORIS (DESY) Synchro-Cyclotron (CERN) E 162 (e-) PRIN-STAN (Stanford) MPQ Betatron (Kerst) ACO (France) LOA VEPP II (Novosibirsk) L’OASIS RAL E 162 (e+) UCLA KEK ILE Betatron (Kerst & Serber) Electrostatic (Van de Graaf) Rectifier (Cockcroft & Walton) LLNL Alternating-Field (Wideroe) 4 10 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 Year of Completion Rasmus Ischebeck > Accelerator R&D Towards Highest Energies. SWHEPPS, 2016 -05 -09 35