1 2 12 2020 TRGONOMET R retim Teknolojileri

1 2. 12. 2020 TRİGONOMET Rİ Öğretim Teknolojileri ve Materyal Tasarımı Mustafa Kerem Özgün

İçerikler KAVRAM HARİTASI …. . 3 YÖNLÜ AÇI Derece, Dakika ve Saniye …. . 6 ii. Derece ile Radyanın İlişkisi …. . 9 iii. Esas Ölçü …. . 12 TRİGONOMETRİK FONKSİYONLAR i. Birim Çember …. . 15 ii. Sinüs ve Kosinüs Fonksiyonları …. . 18 iii. Tanjant ve Kotanjant Fonksiyonları …. . 21 iv. Sinüs Teoremi …. . 26 v. Kosinüs Teoremi …. . 29 vi. Tek ve Çift Fonksiyonlar …. . 33 vii. Ters Trigonometrik Fonksiyonlar …. . 36 viii. Grafik Çizimi …. . 42 KAVRAM KARİKATÜRÜ …. . 45 ÇENGEL BULMACA …. . 46 PETEK BULMACA …. . 48 DEĞERLENDİRME …. . 49 İLETİŞİM …. . 50 2. 12. 2020 i. 2

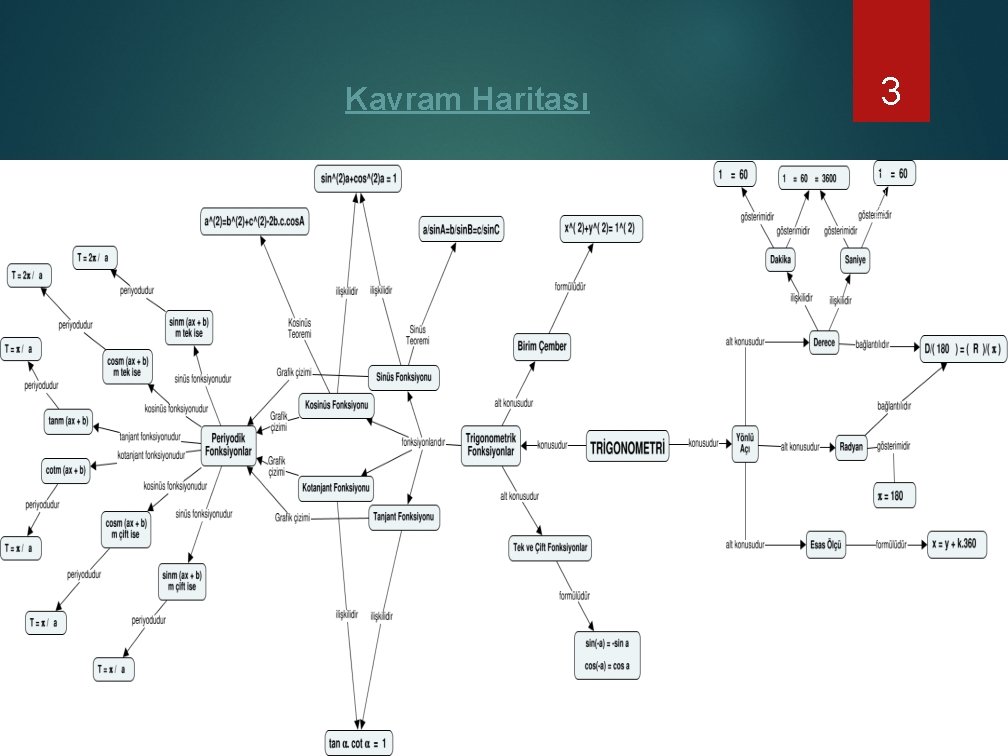
Kavram Haritası 3 2. 12. 2020

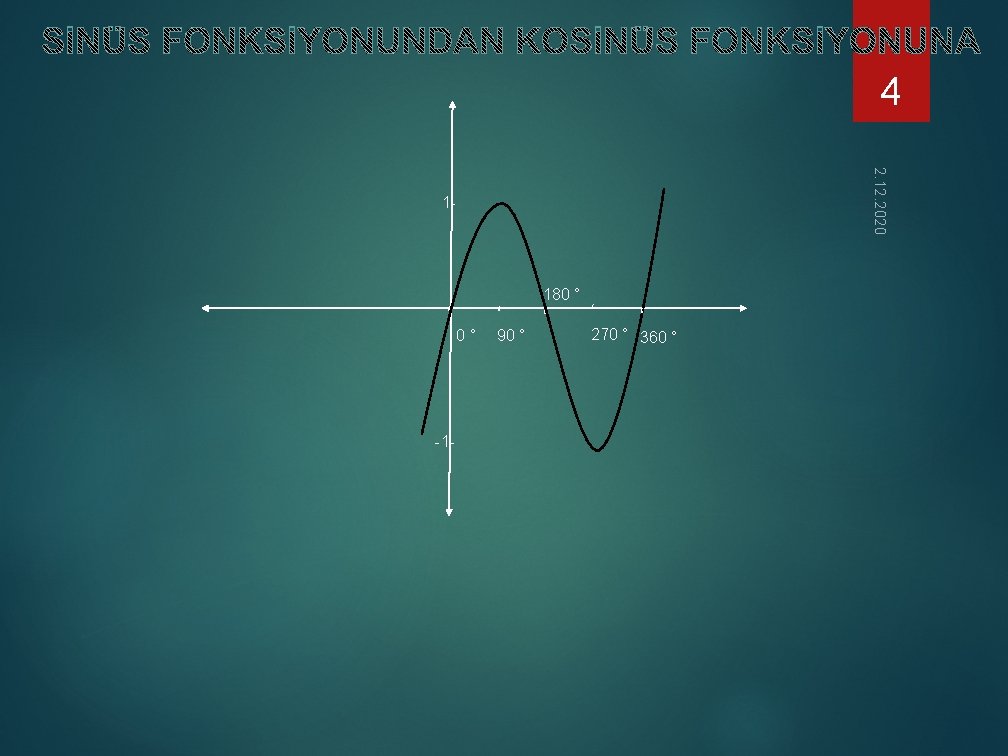
5 İZLEMEK İÇİN Bu videoyu izleyin ve sin 0 ° , sin 30 °, sin 45 °, sin 60 ° , sin 90 ° ile cos 0 °, cos 30 °, cos 45 °, cos 60 °, cos 90 ° değerlerini bulup, kağıt üzerine çizip getiriniz. 2. 12. 2020 SİNÜS VE KOSİNÜS FONKSİYONLARININ DEĞERLERİNİ BULMAK İÇİN UYGULANILABİLECEK PÜF NOKTA

6 Derece, Dakika ve Saniye 2. 12. 2020 Derece: Bir tam çember yayının 360 eş parçasının birini gören merkez açının ölçüsüne 1 derece denir. 1 ° ile gösterilir. Dakika: 1 derece 60 dakikaya eşittir. 1° = 60' eşitliği vardır. Saniye: 1 dakika 60 saniyeye, 1 derece ise 3600 saniyeye eşittir. 1' = 60'' eşitliği vardır. 1° = 60' , 1' = 60'' olduğundan 1° = 60' = 3600'' olarak kullanılır.

Örnek 1 7 2. 12. 2020 28° 52' 32'' + 32° 55' 29'' = ? 53° 47' 23'' 52° 47' 1'' 51° 49' 1'' 50° 37' 12'' 42° 27' 1'' CEVABI GÖRMEK İÇİN TIKLAYIN

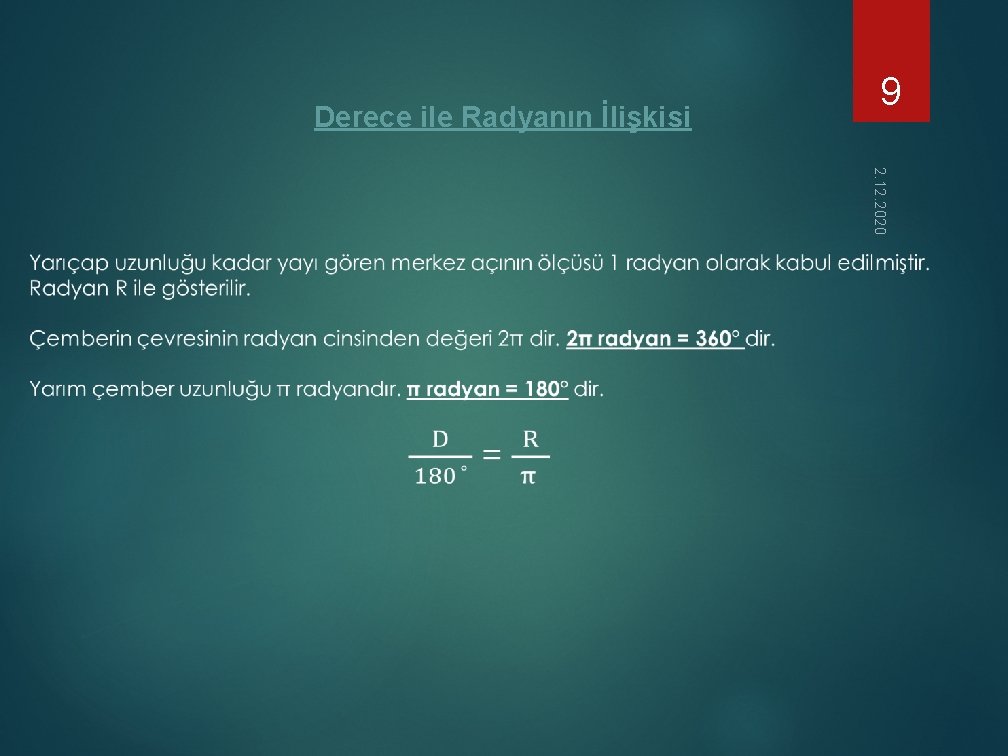
Derece ile Radyanın İlişkisi 2. 12. 2020 9

Örnek 2 2. 12. 2020 10 CEVABI GÖRMEK İÇİN TIKLAYIN

Esas Ölçü 2. 12. 2020 12

Örnek 3 2. 12. 2020 13 CEVABI GÖRMEK İÇİN TIKLAYIN

Birim Çember Birim çemberin denklemi: x 2 + y 2 = 1 dir. 2. 12. 2020 Analitik düzlemde merkezi O(0, 0) (orijin) ve yarıçapı 1 birim olan çembere birim çember denir. 15

Örnek 4 16 √ 40/3 √ 40/7 √ 30/7 √ 41/7 2. 12. 2020 A(3/7, m) noktası birim çember üzerinde ise m değeri ne olabilir ? √ 39/7 CEVABI GÖRMEK İÇİN TIKLAYIN

Sinüs ve Kosinüs Fonksiyonları 18 2. 12. 2020 A. KOSİNÜS FONKSİYONU Bir x reel sayısını cosx e dönüştüren fonksiyona kosinüs fonksiyonu denir. x = cosa dır. Kosinüs fonksiyonunun görüntü kümesi (aralığı), [– 1, 1] dir. Yani, her için, – 1 < cosa < 1 dir. B. SİNÜS FONKSİYONU Bir x reel sayısını sinx e dönüştüren fonksiyona sinüs fonksiyonu denir. y = sina dır. Sinüs fonksiyonunun görüntü kümesi (aralığı), [– 1, 1] dir. Yani, her için, – 1 < sina < 1 dir.

Örnek 5 19 2. 12. 2020 1) 2) ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Tanjant ve Kotanjant Fonksiyonları 21 2. 12. 2020 C. TANJANT FONKSİYONU Birim çember üzerinde P(x, y) noktası ile eşlenen açı olsun. [OP nın x = 1 doğrusunu kestiği T noktasının ordinatına, a reel (gerçel) sayısının tanjantı denir tana ile gösterilir. x = 1 doğrusuna tanjant ekseni denir. D. KOTANJANT FONKSİYONU Birimçember üzerinde P(x, y) noktası ile eşlenen açı olsun. [OP nın y = 1 doğrusunu kestiği K noktasının apsisine, a reel (gerçel) sayısının kotanjantı denir ve cota ile gösterilir.

Örnek 6 22 2. 12. 2020 2 a+5 -(a+5) -a+1 2 a+1 -(a+1) ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Örnek 7 24 2. 12. 2020 tan 65 ° = a olduğuna göre, tan 40° ’nin a cinsinden değeri nedir? ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Sinüs Teoremi 2. 12. 2020 a, b, ve c üçgenin kenar uzunlukları, A, B ve C üçgenin iç açıları ve r çevrel çemberin yarı çapı ise bunlar arasında sinüs teoremine göre aşağıdaki eşitlik mevcuttur: 26

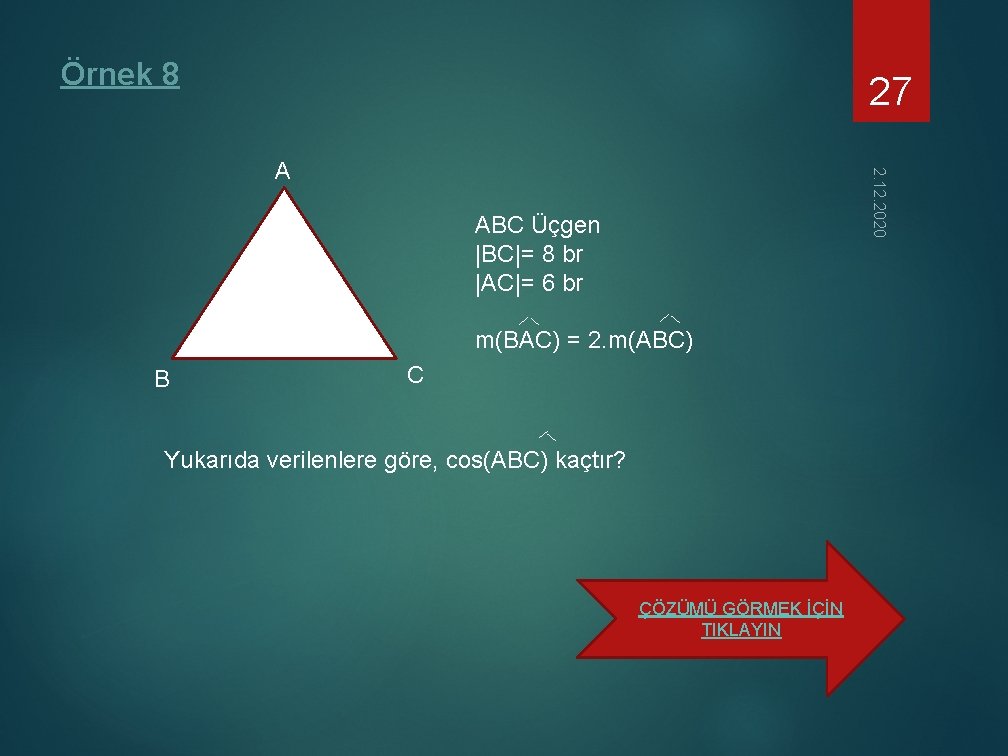
Örnek 8 27 2. 12. 2020 A ABC Üçgen |BC|= 8 br |AC|= 6 br m(BAC) = 2. m(ABC) B C Yukarıda verilenlere göre, cos(ABC) kaçtır? ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Kosinüs Teoremi 2. 12. 2020 29

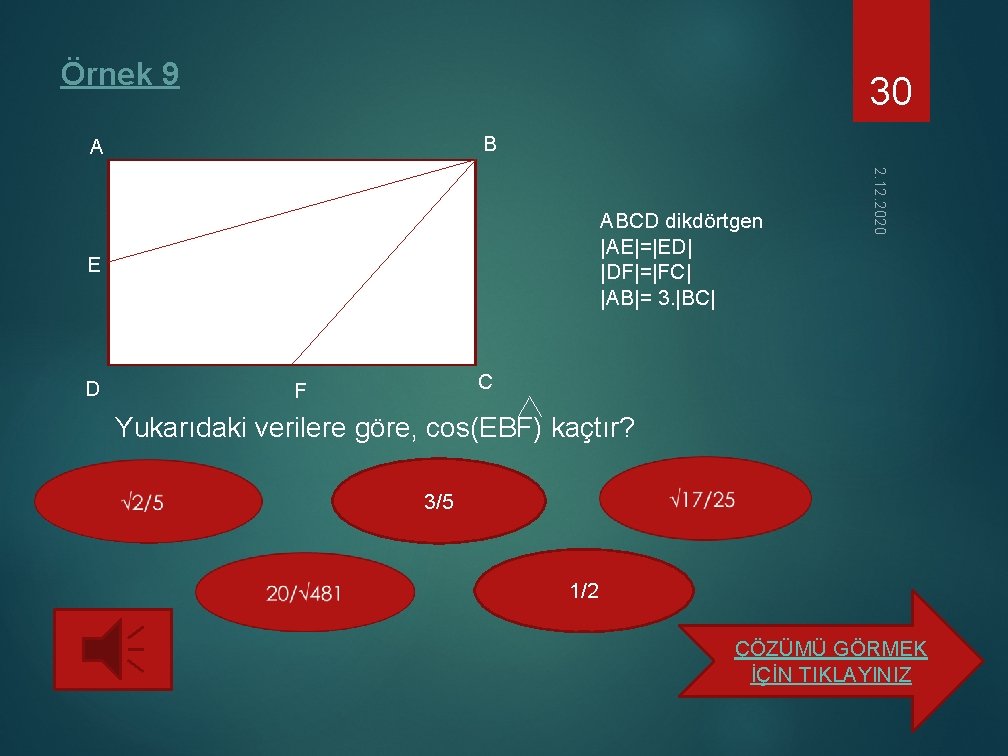
Örnek 9 30 B A E D 2. 12. 2020 ABCD dikdörtgen |AE|=|ED| |DF|=|FC| |AB|= 3. |BC| C F Yukarıdaki verilere göre, cos(EBF) kaçtır? 3/5 1/2 ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYINIZ

Tek ve Çift Fonksiyonlar 33 2. 12. 2020 A) Tek Fonksiyon f(–x) = – f(x) ise f fonksiyonuna tek fonksiyon denir. Tek fonksiyonlar çift dereceli olamaz. B) Çift Fonksiyon f(–x) = f(x) ise f fonksiyonuna çift fonksiyon denir. Çift fonksiyonlar tek dereceli olamaz.

Örnek 10 34 2. 12. 2020 Aşağıdakilerden hangisi çift fonksiyondur? 2 x-1 x+3 ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Ters Trigonometrik Fonksiyonlar ARKKOSİNÜS FONKSİYONU f– 1(x) = cos– 1 x veya f– 1(x) = arccosx şeklinde gösterilir. ARKTANJANT FONKSİYONU f– 1(x) = tan– 1 x veya f– 1(x) = arctanx şeklinde gösterilir. ARKKOTANJANT FONKSİYONU f– 1(x) = cot– 1 x veya f– 1(x) = arccotx şeklinde gösterilir. 2. 12. 2020 ARKKOSİNÜS FONKSİYONU f– 1(x) = sin– 1 x veya f– 1(x) = arcsinx şeklinde gösterilir. 36

Örnek 11 2. 12. 2020 37 ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYIN

Örnek 12 2. 12. 2020 39 ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYINIZ

Trigonometrik Fonksiyonların Grafik Çizimi 1. Fonksiyonun esas periyodu bulunur. 2. Bulunan periyoda uygun bir aralık seçilir. 3. Seçilen aralıkta fonksiyonun değişim tablosu yapılır. 4. Seçilen bir periyotluk aralıkta fonksiyonun grafiği çizilir. 2. 12. 2020 Trigonometrik fonksiyonların grafikleri çizilirken, 42

Örnek 13 2. 12. 2020 43 ÇÖZÜMÜ GÖRMEK İÇİN TIKLAYINIZ

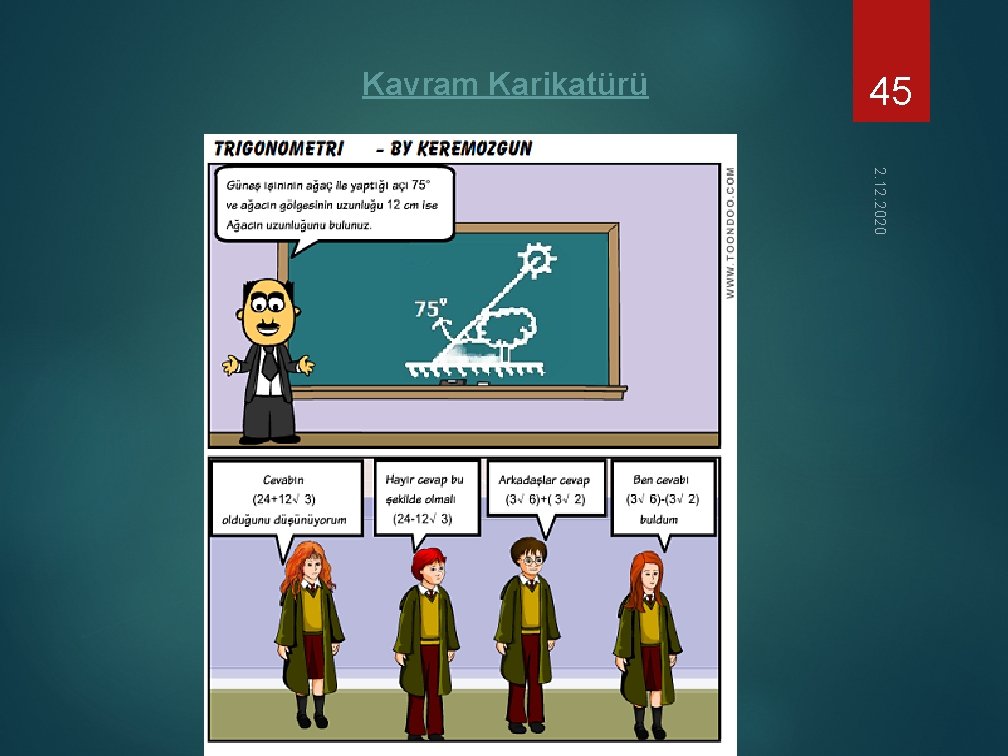
Kavram Karikatürü 45 2. 12. 2020

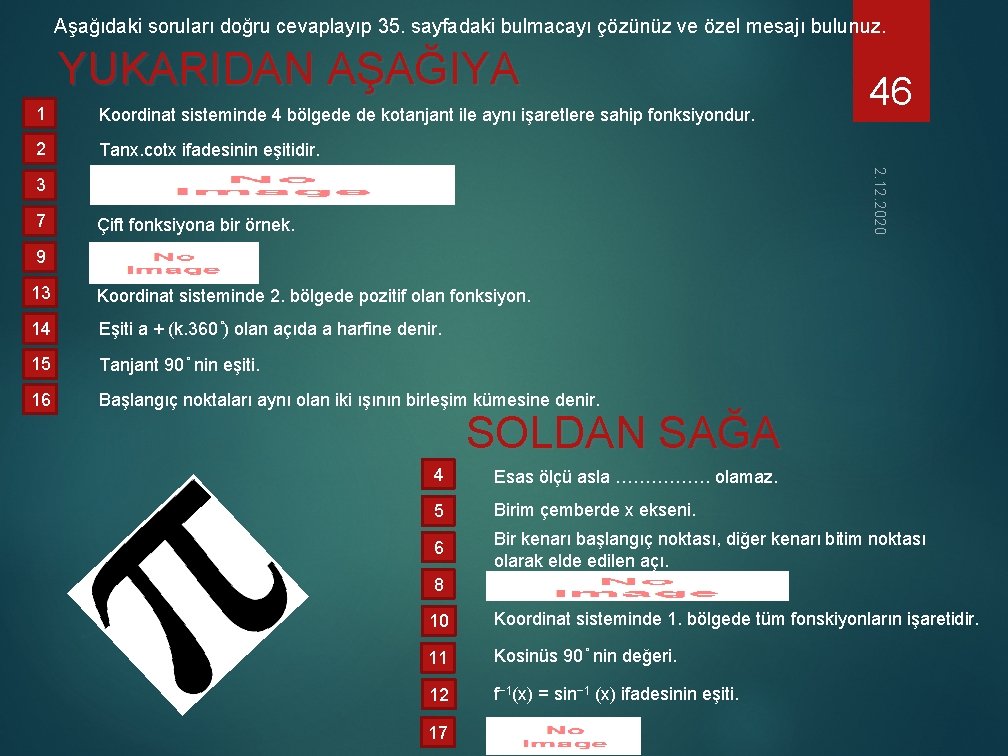
Aşağıdaki soruları doğru cevaplayıp 35. sayfadaki bulmacayı çözünüz ve özel mesajı bulunuz. YUKARIDAN AŞAĞIYA Koordinat sisteminde 4 bölgede de kotanjant ile aynı işaretlere sahip fonksiyondur. 2 Tanx. cotx ifadesinin eşitidir. 3 7 Çift fonksiyona bir örnek. 9 13 Koordinat sisteminde 2. bölgede pozitif olan fonksiyon. 14 Eşiti a + (k. 360 ) olan açıda a harfine denir. 15 Tanjant 90 nin eşiti. 16 Başlangıç noktaları aynı olan iki ışının birleşim kümesine denir. 46 2. 12. 2020 1 SOLDAN SAĞA 4 Esas ölçü asla ……………. olamaz. 5 Birim çemberde x ekseni. 6 Bir kenarı başlangıç noktası, diğer kenarı bitim noktası olarak elde edilen açı. 8 10 Koordinat sisteminde 1. bölgede tüm fonskiyonların işaretidir. 11 Kosinüs 90 nin değeri. 12 f− 1(x) = sin− 1 (x) ifadesinin eşiti. 17

15 7 1 17 3 12 2 47 16 2. 12. 2020 11 4 13 9 10 14 5 6 ÖZEL CEVAP

Aşağıda trigonometri ile ilgili saklanan kelimeleri bulunuz ve üstlerini çiziniz E S Ö S N İ N Ü A Ç M R A T K E J Ü N İ S O Ü Ö Y L Y Ü Y O Ç S E Y N A İ O L S K F Ö N K S R M S A O Ç S N R T B İ E E Ç T Y R I A O İ P B L S E S T Ü I A A N 2. 12. 2020 Y 48

Değerlendirme 49 2. 12. 2020 DEĞERLENDİRME TESTİNİ İNDİRMEK İÇİN TIKLAYINIZ. .

50 2. 12. 2020 İletişim; Blog: www. pikare. wordpress. com E-posta: kerem. ozgun. 78@hotmail. com Gmail: keremozgun 78@gmail. com İyi Çalışmalar…